Презентація на тему:
Його величність - трикутник

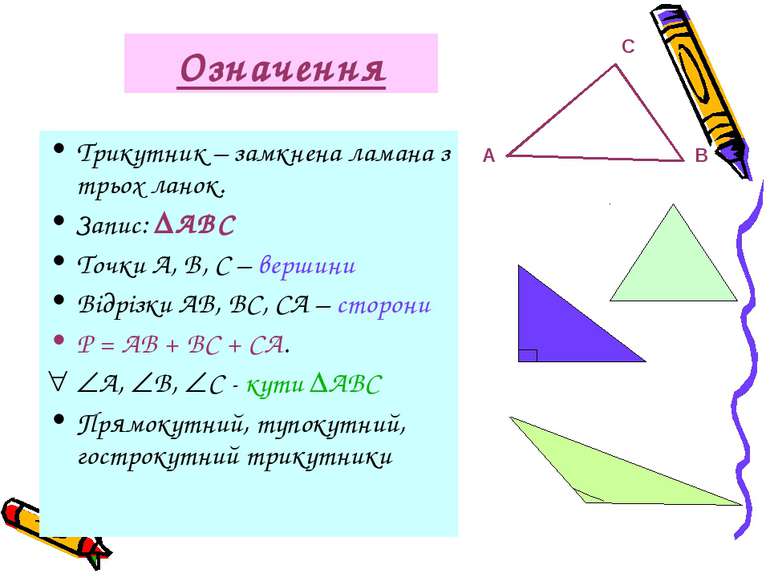
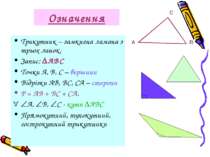
Означення Трикутник – замкнена ламана з трьох ланок. Запис: АВС Точки А, В, С – вершини Відрізки АВ, ВС, СА – сторони Р = АВ + ВС + СА. А, В, С - кути АВС Прямокутний, тупокутний, гострокутний трикутники С В А

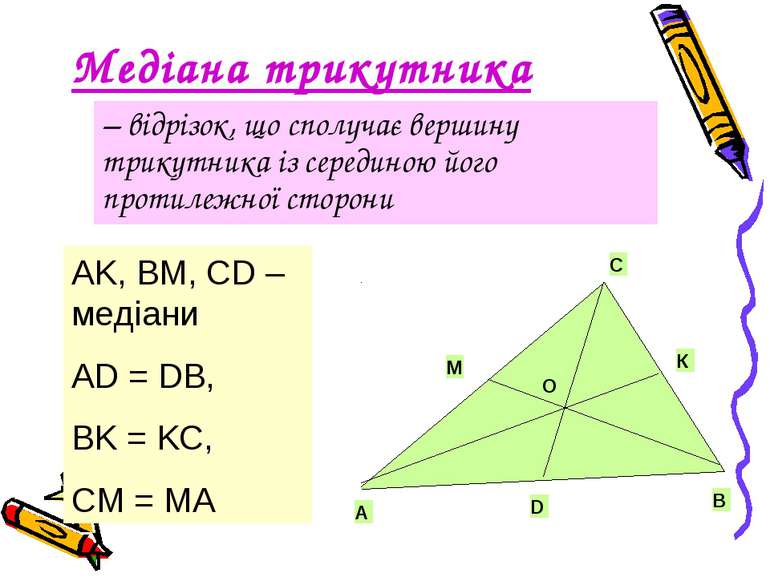
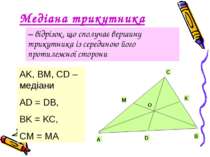
Медіана трикутника – відрізок, що сполучає вершину трикутника із серединою його протилежної сторони AK, BM, CD –медіани AD = DB, BK = KC, CM = MA

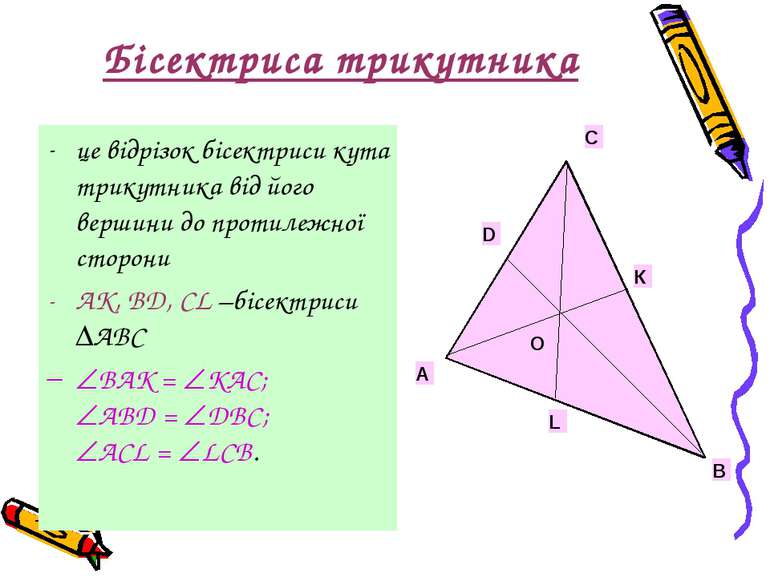
Бісектриса трикутника це відрізок бісектриси кута трикутника від його вершини до протилежної сторони AK, BD, CL –бісектриси ABC BAK = KAC; ABD = DBC; ACL = LCB.

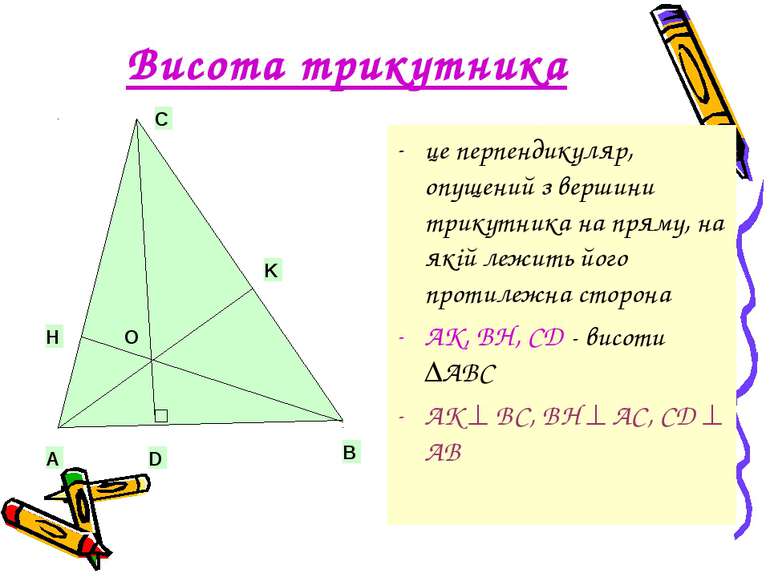
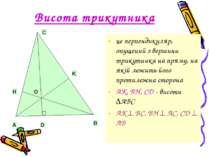
Висота трикутника це перпендикуляр, опущений з вершини трикутника на пряму, на якій лежить його протилежна сторона AK, BH, CD - висоти ABC AK BC, BH AC, CD AB

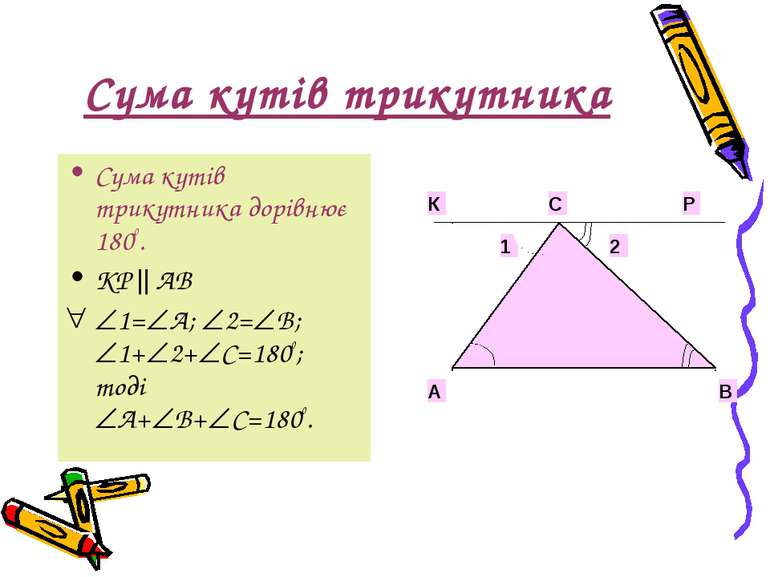
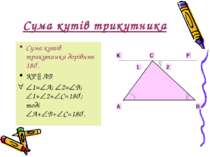
Сума кутів трикутника Сума кутів трикутника дорівнює 180о. КР АВ 1= А; 2= В; 1+ 2+ С=180о; тоді А+ В+ С=180о.

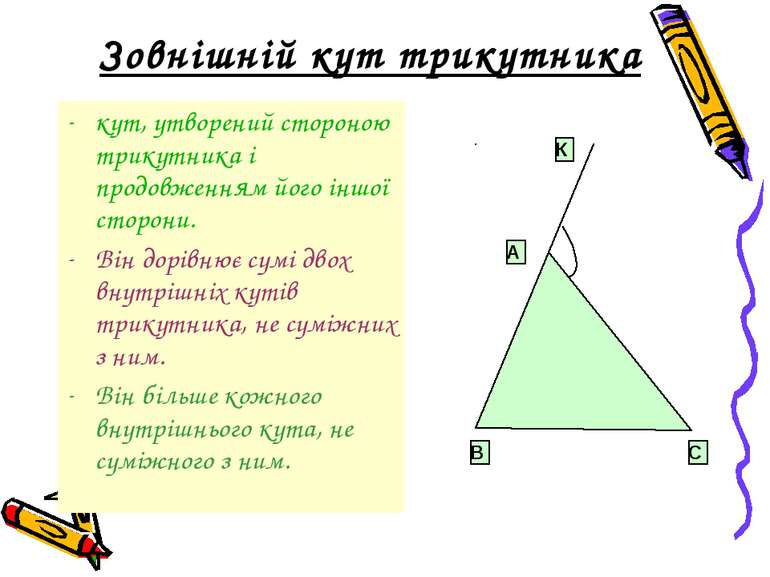
Зовнішній кут трикутника кут, утворений стороною трикутника і продовженням його іншої сторони. Він дорівнює сумі двох внутрішніх кутів трикутника, не суміжних з ним. Він більше кожного внутрішнього кута, не суміжного з ним.

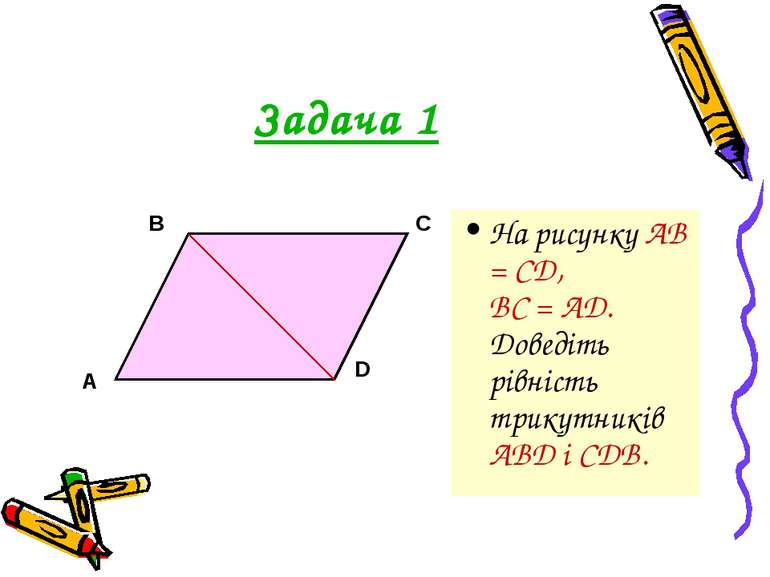
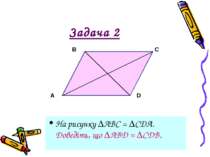
Рівність геометричних фігур Якщо фігури можна сумістити рухом, то вони рівні Якщо кожна з двох фігур дорівнює третій, то перша і друга фігури рівні. ABC = КРТ, тоді розуміють, що А = К, В = Р, С = Т, АВ = КР, АС = КТ, ВС = РТ.

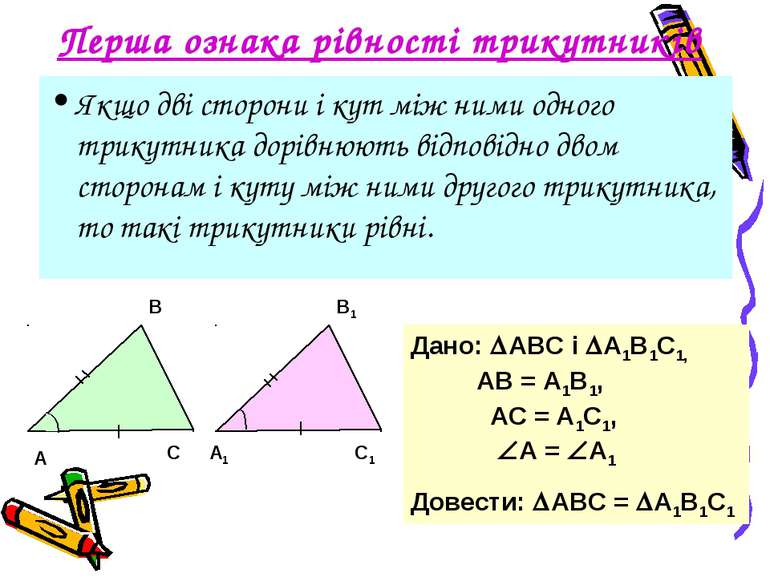
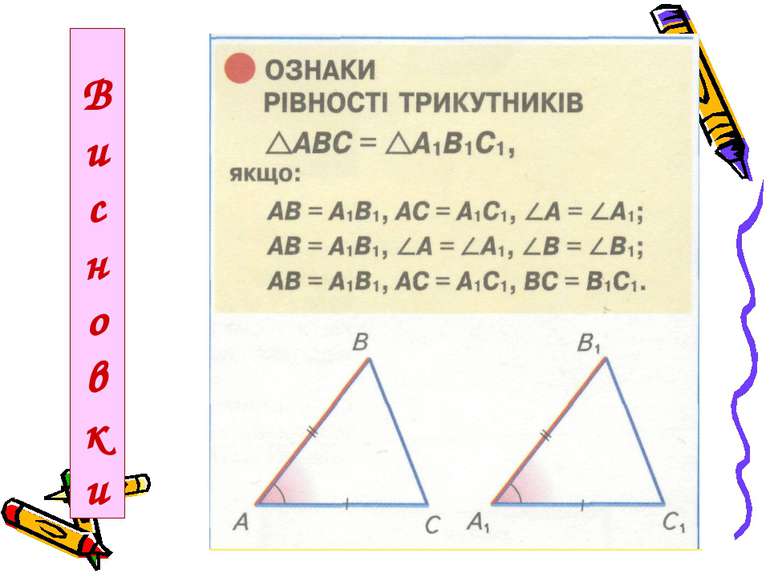
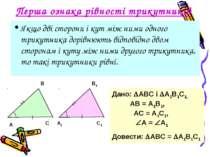
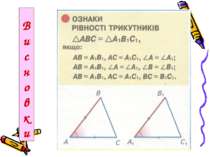
Перша ознака рівності трикутників Якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні. Дано: АВС і А1В1С1, АВ = А1В1, АС = А1С1, А = А1 Довести: АВС = А1В1С1

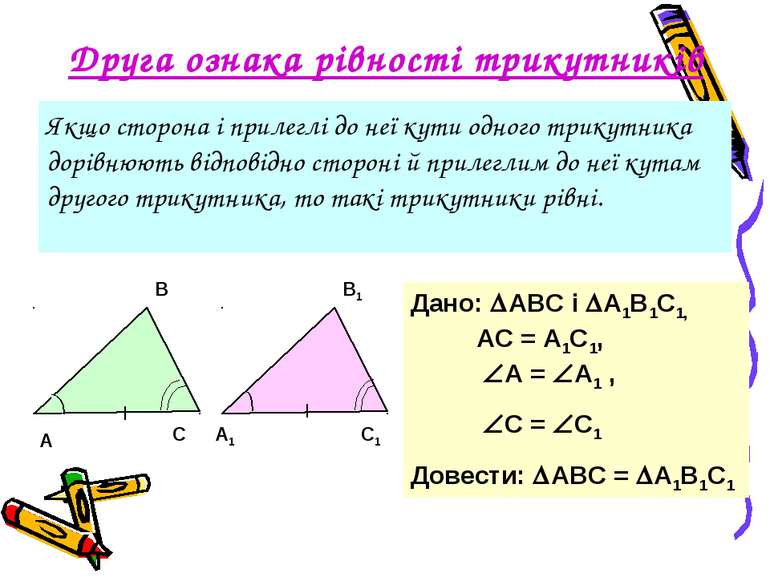
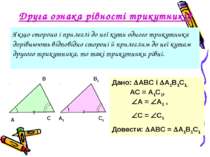
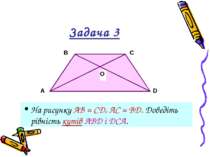
Друга ознака рівності трикутників Якщо сторона і прилеглі до неї кути одного трикутника дорівнюють відповідно стороні й прилеглим до неї кутам другого трикутника, то такі трикутники рівні. Дано: АВС і А1В1С1, АС = А1С1, А = А1 , C = C1 Довести: АВС = А1В1С1

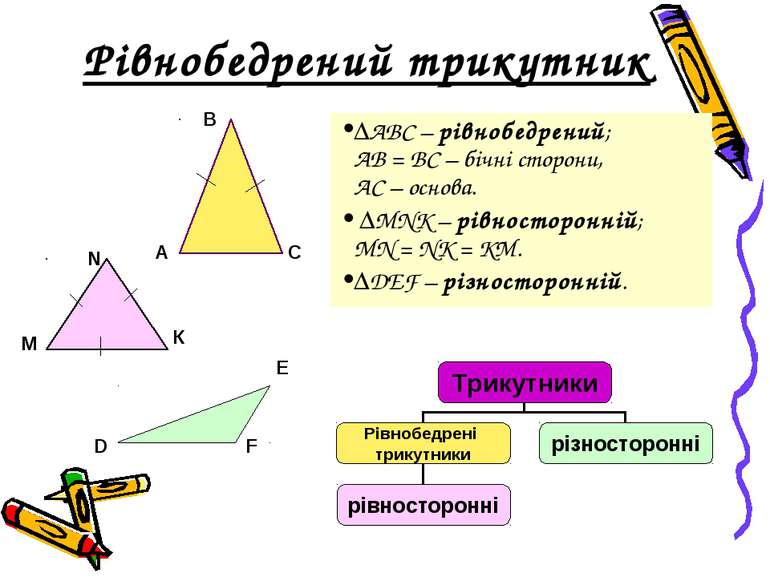
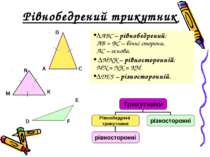
Рівнобедрений трикутник ΔАВС – рівнобедрений; АВ = ВС – бічні сторони, АС – основа. ΔMNK – рівносторонній; MN = NK = KM. ΔDEF – різносторонній.

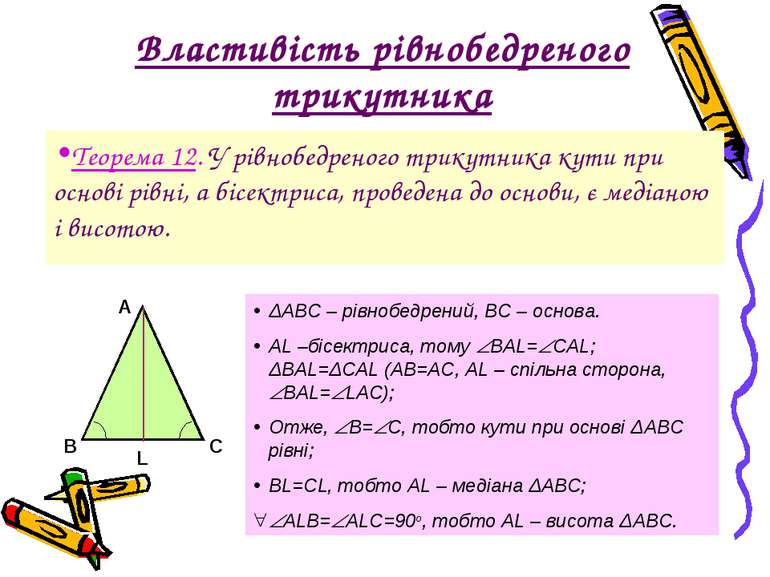
Властивість рівнобедреного трикутника Теорема 12. У рівнобедреного трикутника кути при основі рівні, а бісектриса, проведена до основи, є медіаною і висотою. ΔАВС – рівнобедрений, ВС – основа. АL –бісектриса, тому ВАL= CAL; ΔBAL=ΔCAL (AB=AC, AL – спільна сторона, ВАL= LAC); Отже, В= С, тобто кути при основі ΔАВС рівні; BL=CL, тобто AL – медіана ΔАВС; ALB= ALC=90o, тобто AL – висота ΔАВС.

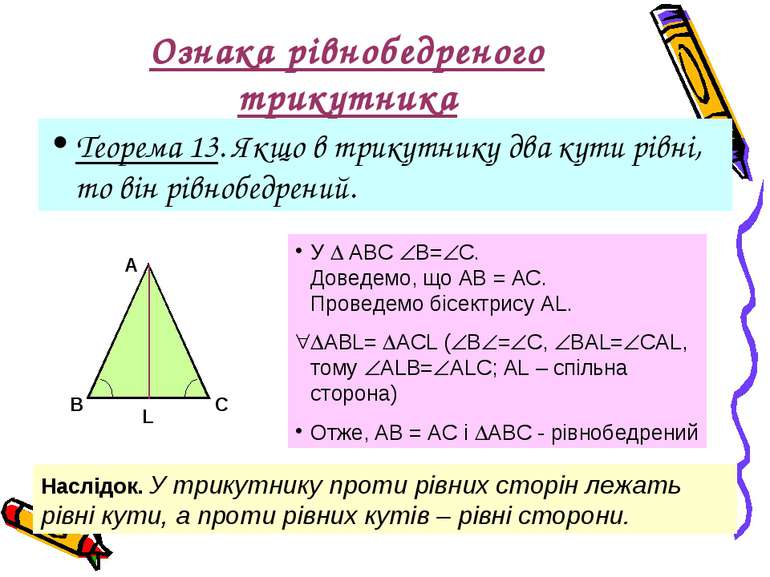
Ознака рівнобедреного трикутника Теорема 13. Якщо в трикутнику два кути рівні, то він рівнобедрений. У АВС В= С. Доведемо, що АВ = АС. Проведемо бісектрису AL. АВL= ACL ( B = C, BAL= CAL, тому ALB= ALC; AL – спільна сторона) Отже, АВ = АС і АВС - рівнобедрений Наслідок. У трикутнику проти рівних сторін лежать рівні кути, а проти рівних кутів – рівні сторони.

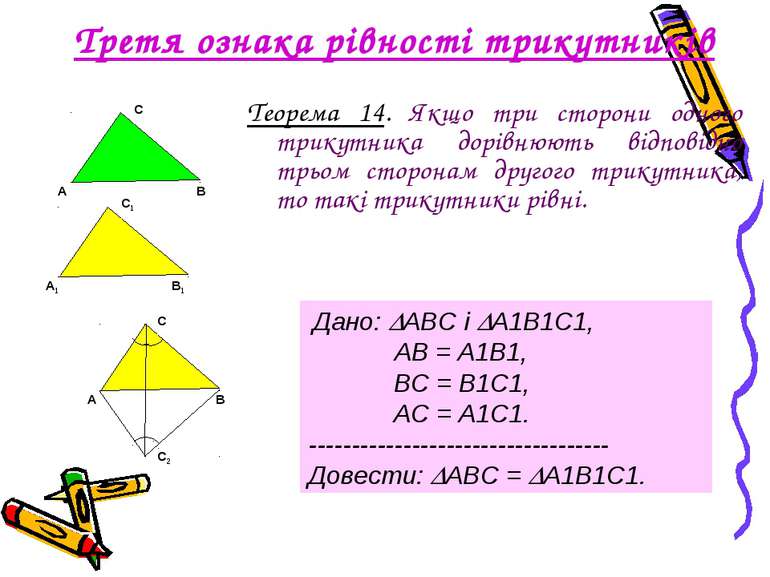
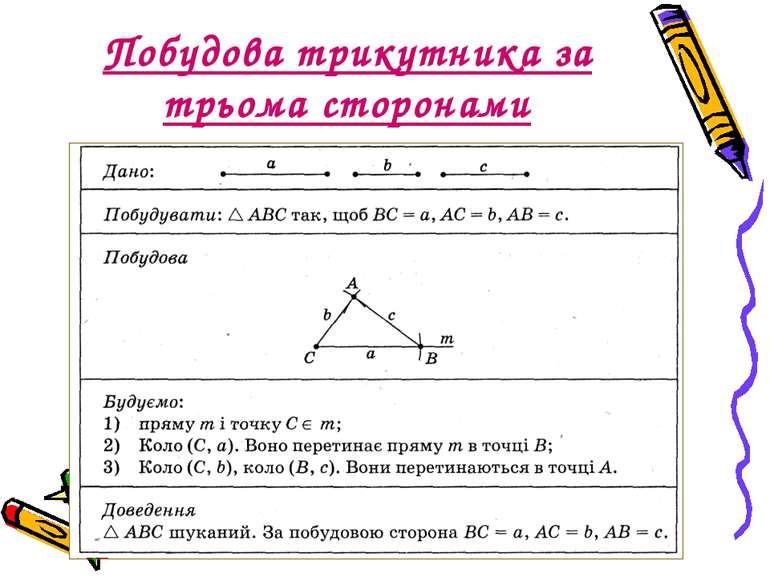
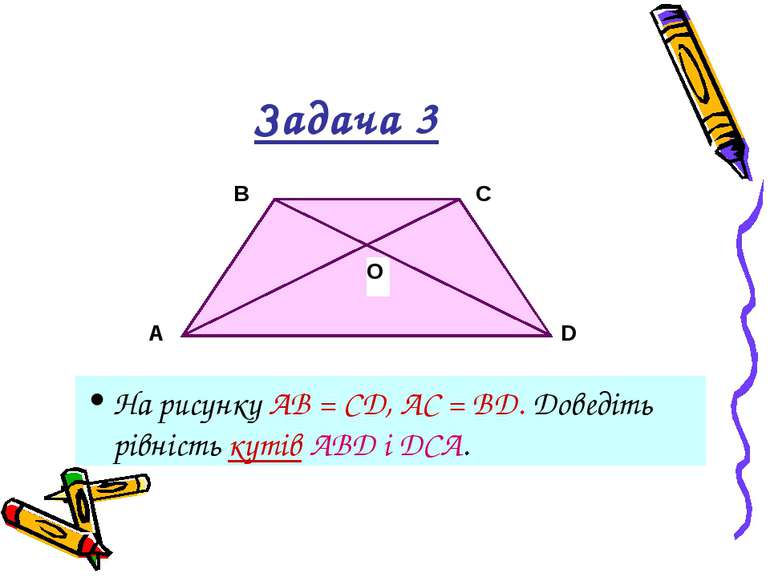
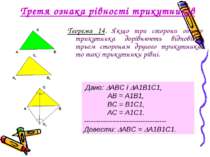
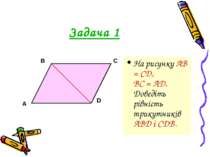
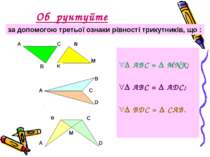
Третя ознака рівності трикутників Теорема 14. Якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам другого трикутника, то такі трикутники рівні. Дано: АВС і А1В1С1, АВ = А1В1, ВС = В1С1, АС = А1С1. ----------------------------------- Довести: АВС = А1В1С1.

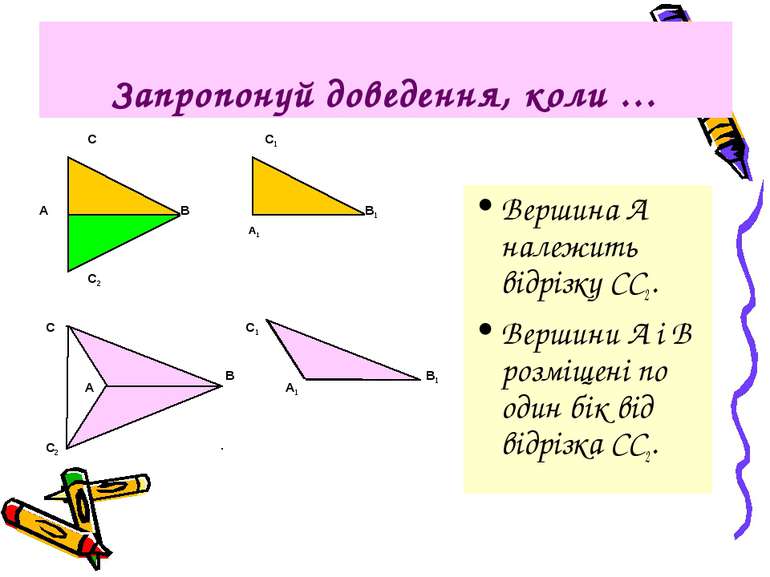
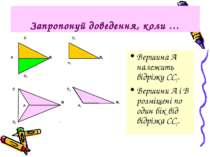
Запропонуй доведення, коли … Вершина А належить відрізку СС2. Вершини А і В розміщені по один бік від відрізка СС2.

Побудова трикутника за трьома сторонами

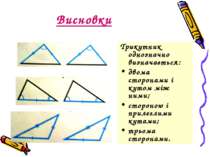
Висновки Трикутник однозначно визначається: двома сторонами і кутом між ними; стороною і прилеглими кутами; трьома сторонами.

Застосуй отримані знання У трикутниках АВС і А1В1С1 АС = А1С1, ВС = В1С1. Яку рівність необхідно додати до умови, щоб рівність даних трикутників можна було довести за третьою ознакою? Три сторони одного трикутника дорівнюють трьом сторонам другого трикутника. Чи є рівними кути між відповідно рівними сторонами цих трикутників? Чому?

Застосуй отримані знання Чи правильно, що два рівносторонні трикутники рівні, якщо вони мають однакові периметри? Чи правильно, що два довільні трикутники рівні, якщо вони мають однакові периметри? Чи виконується обернене твердження?

Задача 1 На рисунку АВ = CD, BC = AD. Доведіть рівність трикутників ABD і CDB.

Задача 2 На рисунку АВС = CDA. Доведіть, що ABD = CDB.

Задача 3 На рисунку АВ = CD, AC = BD. Доведіть рівність кутів ABD і DCA.

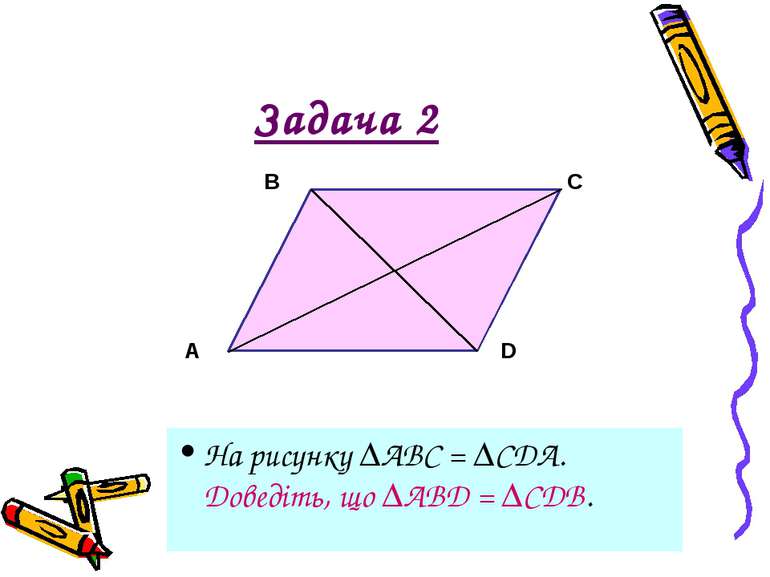
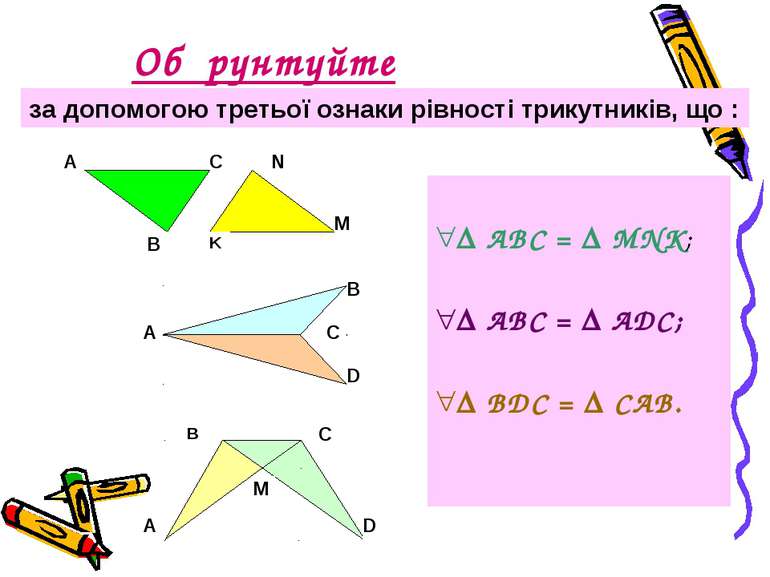
Обґрунтуйте АВС = MNK; АВС = ADC; BDC = CAB. за допомогою третьої ознаки рівності трикутників, що :

Висновки