Презентація на тему:
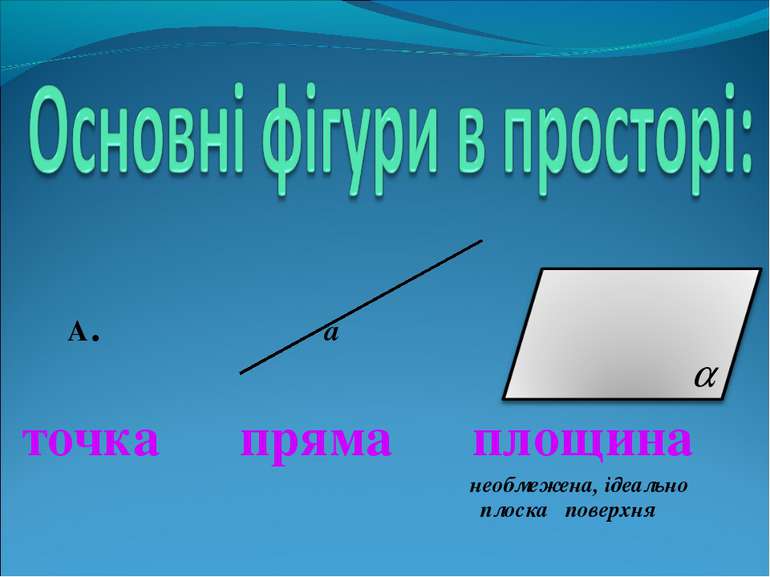
Вступ до стереометрії. Визначення

Стереометрія – від грецького – тіло, μετρεο – вимірюю – вимірювання тіл.

A. a точка пряма площина необмежена, ідеально плоска поверхня

Яка б не була площина, існують точки, що належать цій площині і точки, які не належать їй. А , С , В , D . А С . . В D . .

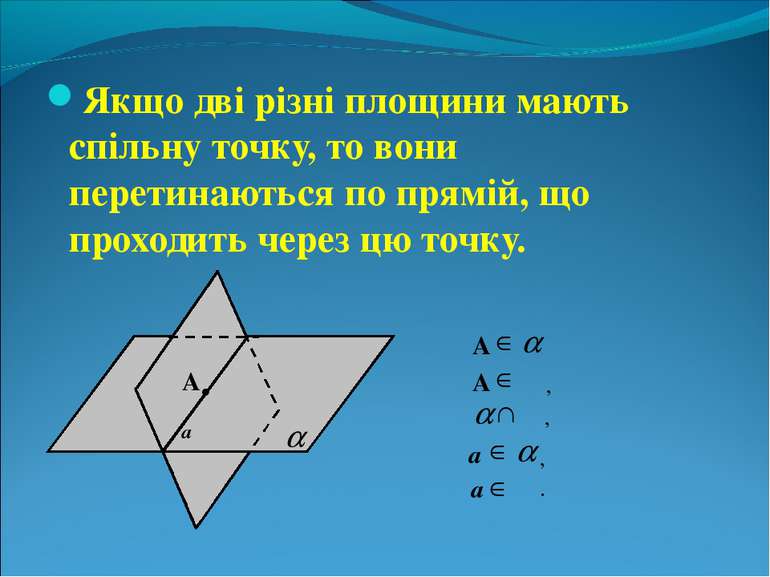
Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку. А . β a А β , β , a , a β . А

Якщо дві різні прямі перетинаються, то через них можна провести площину, і до того ж тільки одну. а b . а , b . a b ,

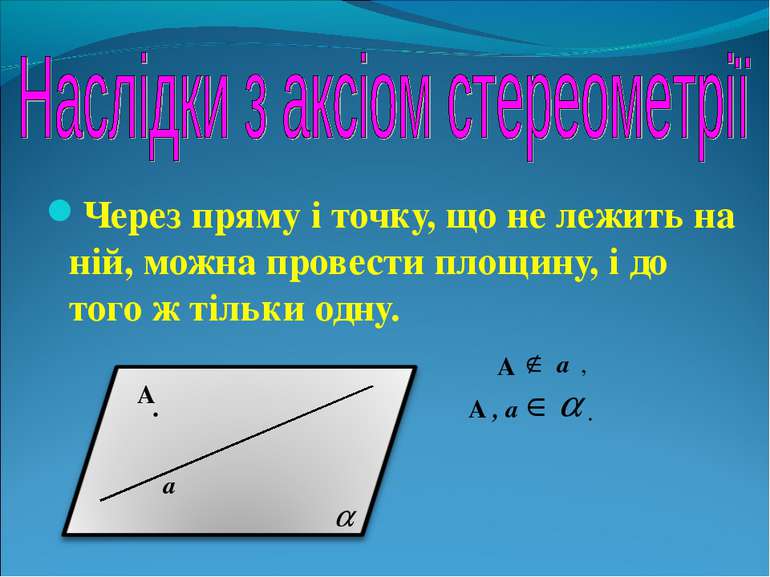
Через пряму і точку, що не лежить на ній, можна провести площину, і до того ж тільки одну. а . А А а , А , а .

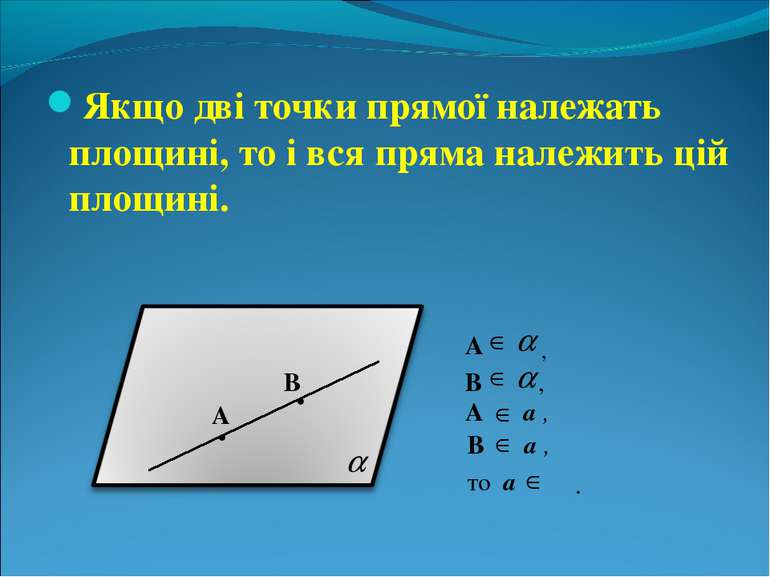
Якщо дві точки прямої належать площині, то і вся пряма належить цій площині. . . А В , В , А А а , В а , то а α .

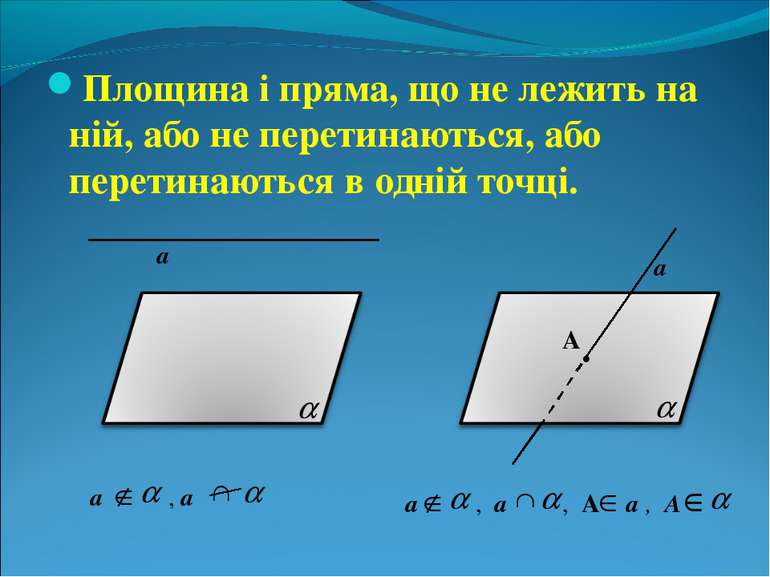
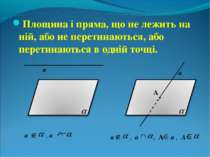
Площина і пряма, що не лежить на ній, або не перетинаються, або перетинаються в одній точці. а . а а , а а , а , А а , А А

Через три точки, що не лежать на одній прямій, можна провести площину, і до того ж тільки одну. . . . А В С А, В, С a; А, В, С .

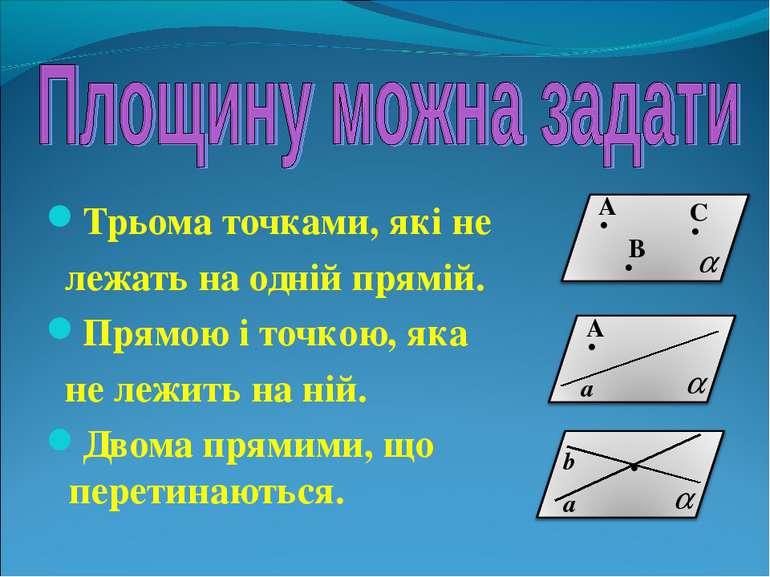
Трьома точками, які не лежать на одній прямій. Прямою і точкою, яка не лежить на ній. Двома прямими, що перетинаються. . . . . A B C a A a b .

Куб А В С D А В С D Вершини А, В, С, … Грані АA B АВСD, … Ребра АВ = СD = АА = … = а а (рівні квадрати) В, d d – діагональ куба

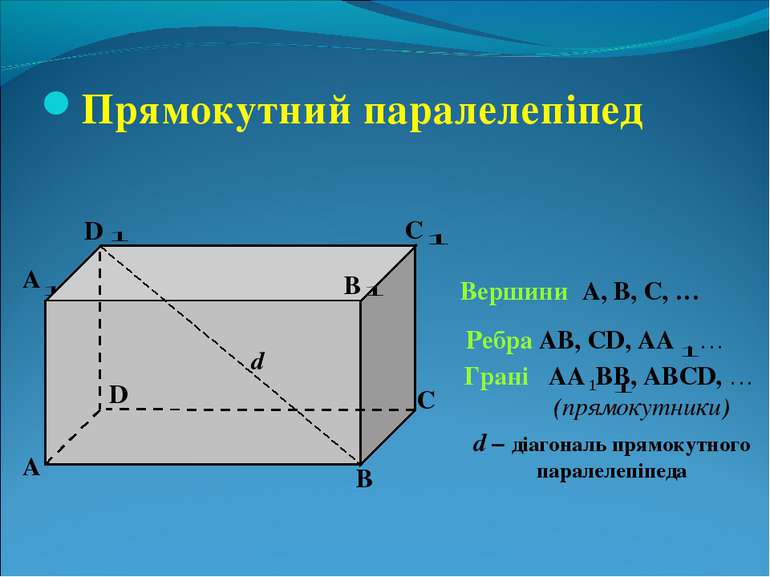
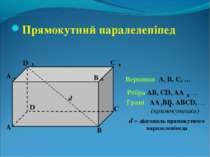
Прямокутний паралелепіпед А В С D А В С D Вершини А, В, С, … B Ребра АВ, СD, АА , … Грані АA (прямокутники) В, ABCD, … d d – діагональ прямокутного паралелепіпеда

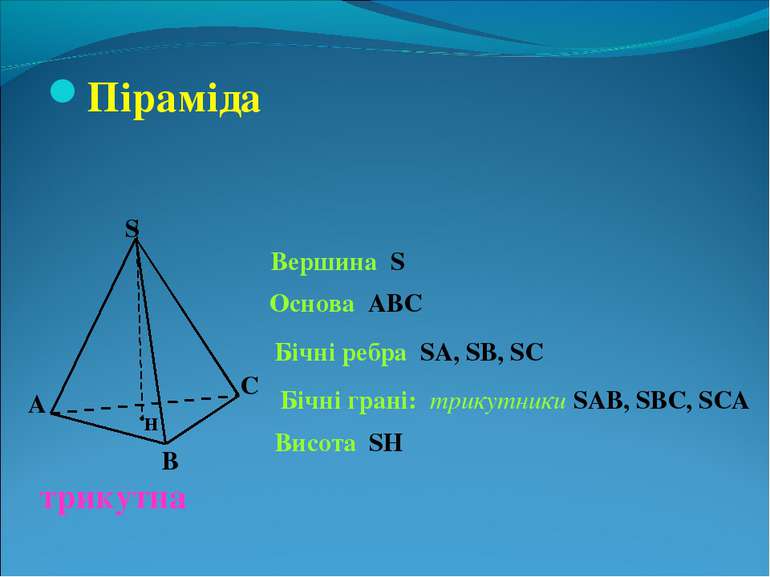
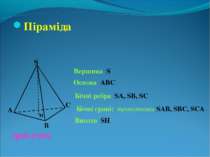
Піраміда S А В С Вершина S Основа АВС трикутна Бічні ребра SA, SB, SC Бічні грані: трикутники SAB, SBC, SCA . н Висота SH

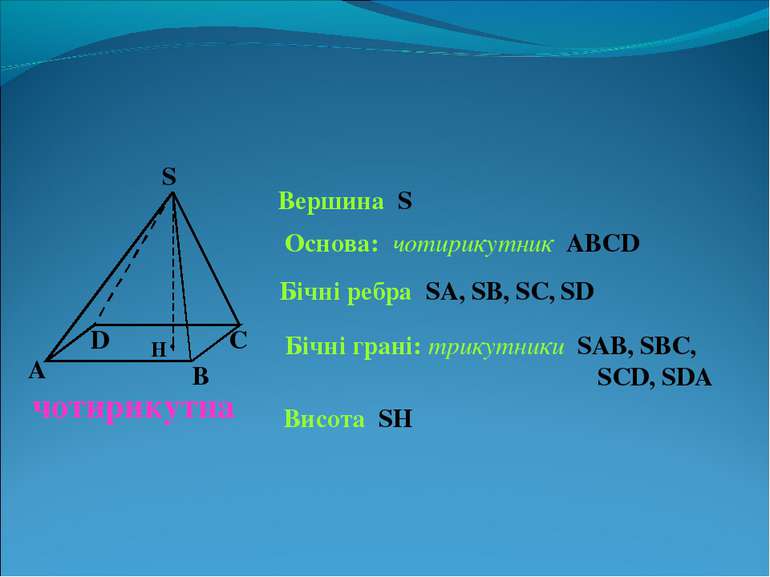
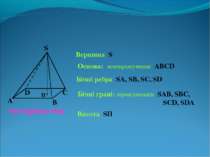
чотирикутна А В С D S Вершина S Основа: чотирикутник АВСD Бічні ребра SA, SB, SC, SD Бічні грані: трикутники SAB, SBC, SCD, SDA Висота SH . Н

Презентацію виконала вчитель математики Чигиринського НВК №2 Захарченко Людмила Олексіївна