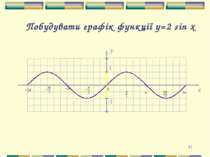
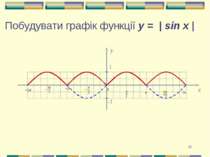
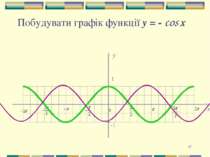
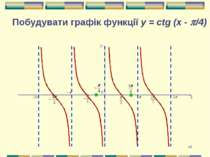
Презентація на тему:
Тригонометричні функції

* Структура навчальної програми № Зміст уроку Кількість годин 1 Радіанне вимірювання кутів. 1 2 Синус, косинус, тангенс, котангенс кута. Тригонометричні функції числового аргументу. 1 3 Основні співвідношення між тригонометричними функціями одного аргументу. 2 4 Формули зведення. 2 5 Періодичність функцій. 1 6 Властивості та графіки тригонометричних функцій. 4 7 Гармонічні коливання. 1

* Навчальні досягнення учнів Виконує перехід від радіанної міри кута до градусної і навпаки. Встановлює відповідність між дійсними числами і точками на одиничному колі. Формулює означення синуса, косинуса, тангенса, котангенса кута і числового аргументу; властивості тригонометричних функцій. Розпізнає і будує графіки тригонометричних функцій і на них ілюструє властивості функцій. Обчислює значення тригонометричних виразів. Перетворює нескладні тригонометричні вирази. Застосовує тригонометричні функції до опису реальних процесів, зокрема гармонічних коливань.

* Пригадаємо У геометрії термін “кут” вживають для позначення двох понять: геометричної фігури, утвореної двома променями із спільним початком (00

* Радіанне вимірювання кутів. У математиці, астрономії, фізиці використовують радіанну міру вимірювання кутів. Перше видання яке містило термін “радіан”, вийшло в 1873 р в Англії. “Радіан” походить від латинського radian (спиця, промінь).

* Це цікаво Існують різні системи вимірювання кутів . Градусне вимірювання і його частини (мінути, секунди) виникло в Стародавньому Вавилоні задовго до нової ери. Жерці вважали, що свій денний шлях Сонце проходить за 180 “кроків”, і, отже, один “крок” дорівнює 1/180 розгорнутого кута. В геометрії як одиницю вимірювання кутів використовують прямий кут (d). Якщоα=300, в одиницях прямого кута позначають так α=⅓ d. В астрономії за одиницю вимірювання кутів взято кутову годину. Це величина кута, який становить 1/6 частину прямого. В техніці за одиницю вимірювання кутів взято повний оберт. В артилерії кути вимірюють в “поділках кутоміра”. Велика поділка – це 1/60 частина повного оберту, мала поділка – 1/100 частини великої поділки (28-32, що означає 28 великих і 32 малих поділок кутоміра). Моряки вимірюють кути в румбах. Ця одинця дорівнює 1/16 частині величини розгорнутого кута. В картографії в деяких країнах за одиницю вимірювання кутів взято град.(g) 1g дорівнює 1/200 частині величини розгорнутого кута (α=5g)

* Радіанне вимірювання кутів Кут 1 радіан – це такий центральний кут, довжина дуги якого дорівнює радіусу кола. 1800=π радіан; 1 радіан = ≈ 570; 10= рад ≈ 0,01745рад α0- градусна міра кута, а – радіанна О R )1рад R Формули переходу від градусної до радіанної міри і навпаки

* Поміркуй Визначити радіанну міру кута 1080. Визначити градусну міру кута 2,3рад

* Виконай самостійно Подай в радіанній мірі величини кутів 360, 600, 2700, 2160. Подай в градусній мірі величини кутів π/12; π/8; 3π/4; -π/9. Перевір себе π/5; π/3; 3π/2; 6π/5. 150; 22,50; 1350; -200.

* Особливості В радіанній системі не введено позначення одиниці вимірювання. Під знаком тригонометричної функції записують тільки числове значення величини кута. Cos π/6; sin2. Одиниця вимірювання радіанної міри міститься у розгорнутому куті не ціле число разів, а ірраціональне: π ≈ 3,14. Для малих кутів, виміряних у радіанах виконуються наближені рівності sinα≈α, tgα≈α. При радіанному вимірюванні кутів спрощується ряд формул . Довжина дуги Площа сектора

* Синус, косинус, тангенс, котангенс “Тригонометрія” (від грецьких слів “тригонон” – трикутник і “метріо” - вимірюю) означає “вимірювання трикутників”. Виникнення тригонометрії пов'язане з розвитком астрономії, зародилась та розвивалась у Вавилоні, Єгипті, Китаї, Індії та інших древніх країнах. Древньогрецькі вчені склали перші тригонометричні таблиці довжин хорд, що відповідають різним центральним кутам кола постійного радіуса, які вони використовували для розв'язування трикутників. Перші таблиці було складено давньогрецьким математиком Гіппархом з Нікеї (ІІ ст. до н.е.). Астроном-математик був засновником математичної географії, склав зірковий каталог, досить точно визначив відстань від Землі до Місяця і ввів географічні координати (широту і довготу), використовуючи складені ним тригонометричні таблиці хорд.

* Синус і косинус зустрічаються в Індійських астрономічних викладах вже з IV-V ст. Синус “ардхаджива”, тобто половина хорди (“джива” – хорда, тятива луку), Це слово було викривлено арабами в “джайб”, що по арабські означає пазуха, опуклість. Слово “джайб” було переведено у XII ст. на латинь відповідним словом “sinus”. Косинус індійці називали “котиджива”, тобто синус залишку (до чверті кола). Від перестановки цих слів і скорочення одного із них (co-sinus) утворився термін “косинус”. У IX-X ст. вчені країн ісламу (ал-Хабаш, ал-Баттані, Абул-Вафа та ін.) ввели нові тригонометричні величини: тангенс (розв´язування задач на визначення довжини тіні) і котангенс, секанс і косеканс. Латинське слово tangens означає дотичний (відрізок дотичної), sekans – січний (відрізок січної). Терміни “котангенс” і “косеканс” були утворені за аналогією з терміном “косинус”.

* Тригонометричні функції числового аргументу Визначення кутів за допомогою прямокутного трикутника. Косинусом кута називається відношення довжини прилеглого катета до довжини гіпотенузи: Синусом кута називається відношення довжини протилежного катета до довжини гіпотенузи: Тангенсом кута називається відношення довжини протилежного катета до довжини прилеглого катета: Котангенсом кута називається відношення довжини прилеглого катета до довжини протилежного катета:

* Визначення тригонометричних функцій на одиничному колі Синусом числа α називають ординату точки Рα одиничного кола, в яку переходить початкова точка Р 0(1;0) при повороті навколо центра кола на кут α радіанів. Його позначають sinα Косинусом числа α називають абсцису точки Р α одиничного кола, в яку переходить початкова точка Р α (1;0) при повороті навколо центра кола на кут α радіанів. Його позначають cosα .

* Визначення тригонометричних функцій на одиничному колі Тангенсом кута називають відношення ординати точки Pα(x;y) до її абсциси. Котангенсом кута називають відношення абсциси точки Pα(x;y) до її ординати. Тангенсом числа α називають відношення sinα до cosα позначають tgα Котангенсом числа α називається відношення cosα до sinα позначають ctgα .

* Лінії тригонометричних функцій для підрахунку кутів та їх знаків в різних чвертях кола Е1АЕ 2 – лінія котангенса D1AD2 – лінія тангенса Лінія косинусів – проекція ОВ рухомого радіуса на горизонтальний діаметр. Лінія синусів – проекція ОА рухомого радіуса на вертикальний діаметр (відповідно до знака).

* Необхідно знати При зростанні α від 00 до 900 – синус кута зростає від 0 до1, косинус спадає від 1 до 0, тангенс… При зростанні α від 900 до 1800 синус кута спадає від 1 до 0, косинус спадає від 0 до -1, тангенс… При зростанні α від 1800 до 2700 синус кута спадає від 0 до -1, косинус зростає від -1 до 0, тангенс… При зростанні α від 2700 до 3600 синус кута зростає від -1 до 0, косинус зростає від 0 до 1, тангенс..

* Виконуємо разом Побудувати на одиничному колі точки Рα, на які відображається точка Р0 при повороті на α радіан, якщо: 1) α= π/12; 2) α=2,5; 3) α=3; 4) α=5π/6. Визначити знаки sinα, cosα, tgα, ctgα якщо α = 0,3; α = 12 π/7; α = -13 π/6. Порівняти : sin1 і sin2; cos2 і cos2,5; tg π/6 і tg, π/4; ctg π/3 і ctg π/3,2.

* Перевір себе Визначити знак виразу: Sin1000Cos2100 Ctg1350 + Tg1450 Sin400 - Sin2100 Sin(-430 0)Tg(-2100) Отримали: < 0 < 0 > 0 > 0

* Основні співвідношення між тригонометричними функціями одного аргументу. ,

* Це цікаво Найбільшими досягненнями грецька тригонометрія зобов’язана Клавдію Птоломею. Його відомий тракат “Мегісте”. Гіпотенузу прямокутного трикутника, яка дорівнює діаметру кола, він записував на основі теореми Піфагора. В сучасному трактуванні Cos2 α + Sin2 α =1

* Усні вправи Чи можуть бути справедлими одночасно рівності: Tgx=3/4 i Cosх=3/5; Tgx=√3 i Sinx=-1/2; Sinx=2/5 i Cosx=4/5

* Виконати завдання Спростити вираз: 1+sin2α – cos2α ; 1 – ctgα*sinα*cosα; (1 – cosα)*tg 2 α*(1 – cosα). Знайти значення всіх тригонометричних функцій аргументу α, якщо sinα= -0,8 і 1800≤α≤2700 Довести тотожність (Ctg2α – cos2α)* tg2α = cos2α

* Формули зведення. Якщо кут α відкладається від вертикального діаметра одиничного кола ( ), то назва даної функції змінюється на кофункцію ; Якщо кут α відкладається від горизонтального діаметра одиничного кола ( ), то назва функції не змінюється. 2. Перед новою функцією записується той знак, який мала функція, що зводилася за умови, що кут α гострий.

* Приведіть до тригонометричних функцій числа α Sin(π\2+α); Cos(3π/2+α); Tg(π - α); Ctg(3π/2 - α); Sin(π+α).

* Обчислити Sin 3000 =sin (3600 - 600)=-sin600 Tg3π/4 = tg(π –π/4) = Cos 1150 = Ctg 7π/4 =

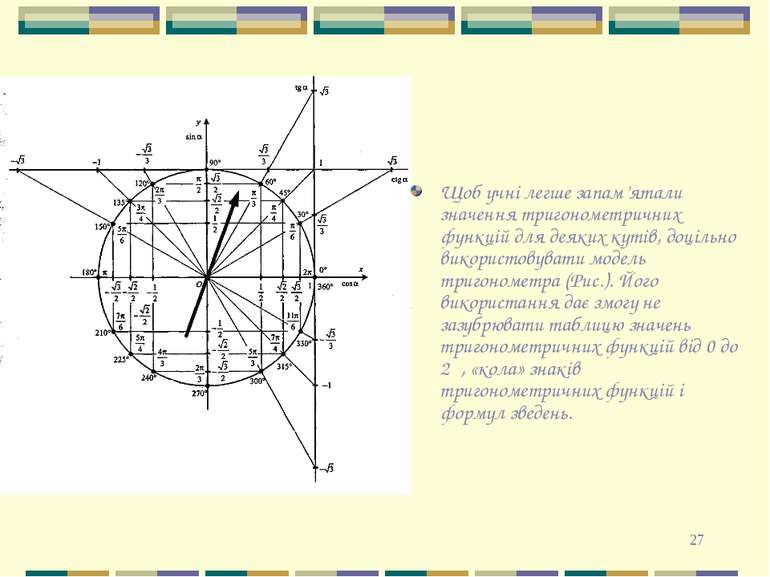
* Щоб учні легше запам’ятали значення тригонометричних функцій для деяких кутів, доцільно використовувати модель тригонометра (Рис.). Його використання дає змогу не зазубрювати таблицю значень тригонометричних функцій від 0 до 2π, «кола» знаків тригонометричних функцій і формул зведень.

* Спростити вираз 1+sin 2 (270 0 – α) + cos 2 (90 0 – α) sin (360 0 - α) + cos (90 0 + α) tg( 3π/2 + α) + ctg (π – α) ctg(5π/2 +α) sin (π/2 + α) - cos (π + α) + tg( π + α)+ + ctg (3π/2 – α)

* Періодичність функцій Т називається періодом функції f(x), якщо для довільного х з області визначення виконується рівність f(x) = f(x + T). Дану функцію називають періодичною. Очевидно, що Т і –Т є періодами (найменшими). Також є періодами числа виду n*T. f(x + 3T) = f((x + 2T) + T) = f(x + 2T) = = f((x + T) + T) = f(x + T) = f(x). Y(x)=f(kx+b) T*=T/lkl

* Тригонометричні функції періодичні Період синуса і косинуса є будь-яке число виду 2πn, n єZ, Тангенса та котангенса є будь-яке число виду 2πn, nєZ. sin(2π+α)=sin α cos(2π + α) =cos α tg( π +α)=tgα ctg(π +α)=ctg α Періодичними бувають не лише тригонометричні функції. Наприклад, функція f(x) = {x} є періодичною з періодом Т = 1.

* Знайти найменший додатній період функцій

* Розв’язуємо разом. №1. Звести до однойменних функцій гострого кута: а) cos1827°=cos(360°*5+27°)= =cos 27°; б) tg 978°=tg(180°*5+78°)= =tg78°; в)   sin (–800°) = г)   ctg 1305° = №2. Обчислити значення тригонометричних функцій: а)   cos 1125° = б)  cos (–315°) = в) tg(-17π/3) = Перевір себе 1.в)sin (–3*360°+280°)= sin280°; г)ctg (7*180°+45°) = ctg45°; 2а) cos (3 * 360° + 45°) = cos 45° = √2/2; б)cos (–360° + 45°) = cos 45°= √2/2; В)√3

* Функція y = sin x Побудова графіка функції

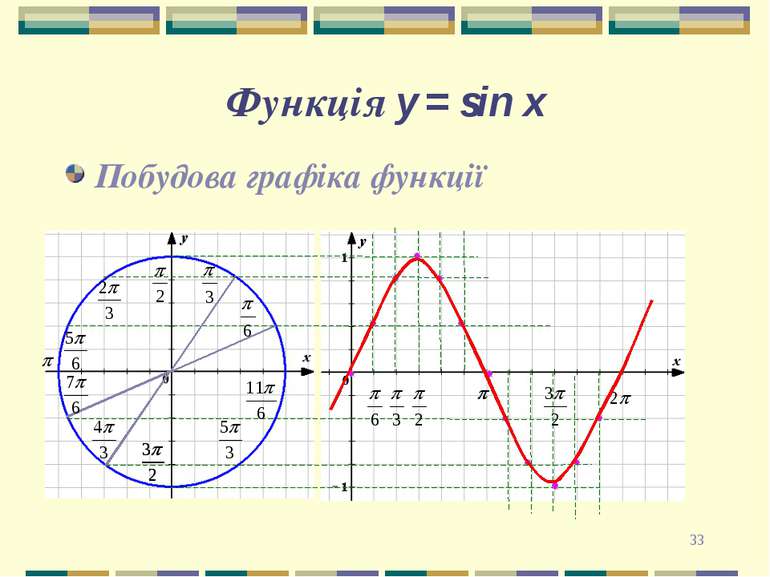
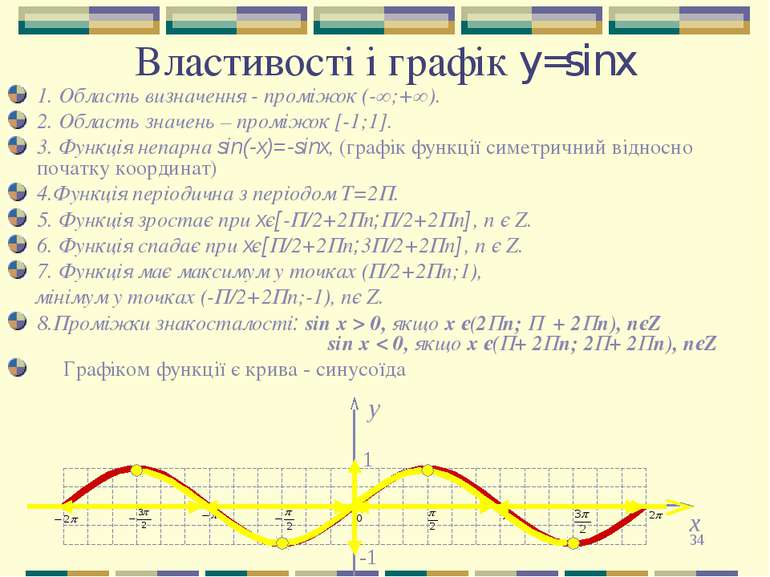
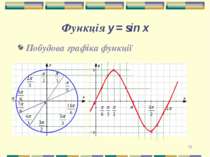
* Властивості і графік y=sinx 1. Область визначення - проміжок (-∞;+∞). 2. Область значень – проміжок [-1;1]. 3. Функція непарна sin(-x)=-sinx, (графік функції симетричний відносно початку координат) 4.Функція періодична з періодом Т=2П. 5. Функція зростає при xє[-П/2+2Пn;П/2+2Пn], n є Z. 6. Функція спадає при xє[П/2+2Пn;3П/2+2Пn], n є Z. 7. Функція має максимум у точках (П/2+2Пn;1), мінімум у точках (-П/2+2Пn;-1), nє Z. 8.Проміжки знакосталості: sin x > 0, якщо х є(2Пn; П + 2Пn), nєZ sin x < 0, якщо x є(П+ 2Пn; 2П+ 2Пn), nєZ Графіком функції є крива - синусоїда

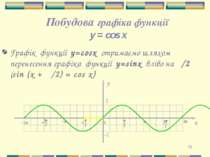
* Побудова графіка функції y = cos x Графік функції у=cosx отримаємо шляхом перенесення графіка функції у=sinx вліво на π/2 (sin (x + π/2) = cos x)

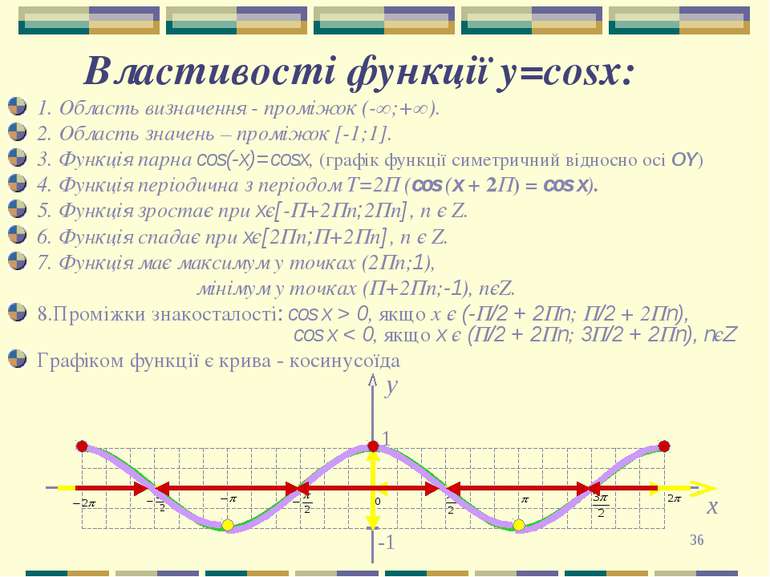
* Властивості функції y=cosх: 1. Область визначення - проміжок (-∞;+∞). 2. Область значень – проміжок [-1;1]. 3. Функція парна cos(-x)=cosx, (графік функції симетричний відносно осі OY) 4. Функція періодична з періодом Т=2П (cos (x + 2П) = cos x). 5. Функція зростає при xє[-П+2Пn;2Пn], n є Z. 6. Функція спадає при xє[2Пn;П+2Пn], n є Z. 7. Функція має максимум у точках (2Пn;1), мінімум у точках (П+2Пn;-1), nєZ. 8.Проміжки знакосталості: cos x > 0, якщо х є (-П/2 + 2Пn; П/2 + 2Пn), cos x < 0, якщо x є (П/2 + 2Пn; 3П/2 + 2Пn), nєZ Графіком функції є крива - косинусоїда

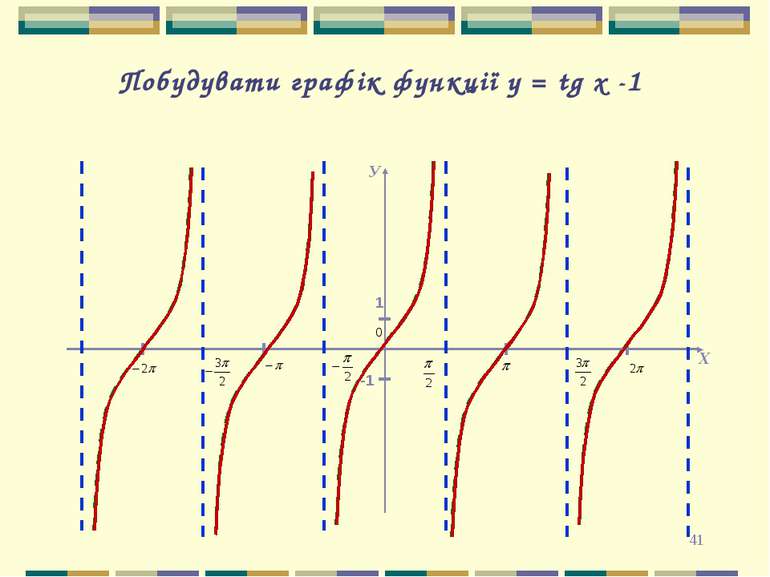
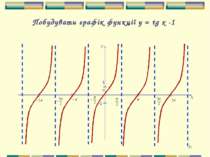
* Властивості функції y=tgх 1. Область визначення – всі дійсні числа, крім точок х=П/2+Пn, nєZ. 2. Область значень – проміжок (-∞;+∞). 3. Функція непарна tg(-х)=-tgх (графік функції симетричний відносно початку координат) 4. Функція періодична з періодом Т= П ( tg(x+π)=tgx). 5. Нулі функції – точки (Пn;0), nєZ. 6.Функція зростає на всій області визначення. 7.Проміжки знакосталості Tg x > 0, якщо х є (Пn; П/2 + Пn), nєZ Tgх < 0, якщо х є (-П/2+Пn;Пn), n є Z. 8. Функція не має екстремумів. 9. Графіком функції є крива – тангенсоїда

* Властивості функції y=ctgх 1. Область визначення – всі дійсні числа, крім точок х=Пn, nєZ. 2. Область значень – проміжок (-∞;+∞). 3. Функція непарна ctg(-х)=-ctgх (графік функції симетричний відносно початку координат ) 4. Функція періодична з періодом Т= П ( сtg(x+π)=сtgx). 5. Нулі функції – точки (π\2+Пn;0), nєZ. 6. Функція спадає на всій області визначення. 7.Проміжки знакосталості ctgх >0, якщо xє (Пn;П/2+Пn), n є Z. ctgх < 0, якщо x є (П/2+Пn;П+Пn), n є Z. 8. Функція не має екстремумів. 9. Графіком функції є крива - котангенсоїда 0 y x

* Користуючись властивостями функцій порівняйте числа: tg 150 і tg 1400 Розв’язання Оскільки tg 1400= tg (1800 - 400)=- tg 400 і tg 150 >- tg 400. Отже, tg 150 > tg 1400. 2. сtg (-1,2 π) і сtg (-0,1π) 3. sin2 і sin5 4. сos70° і сos290° 5. сos340° і sin250°

* Перетворення графіків функцій 1.Для побудови графіка функції y = f(x)± а необхідно виконати паралельне перенесення графіка функції y = f(x) вздовж осі OY на а одиниць вгору (вниз). 2. Для побудови графіка функції y = f(x±а) необхідно виконати паралельне перенесення графіка функції y = f(x) вздовж осі OX на а одиниць вліво (вправо).

* Побудувати графік функції y = tg x -1

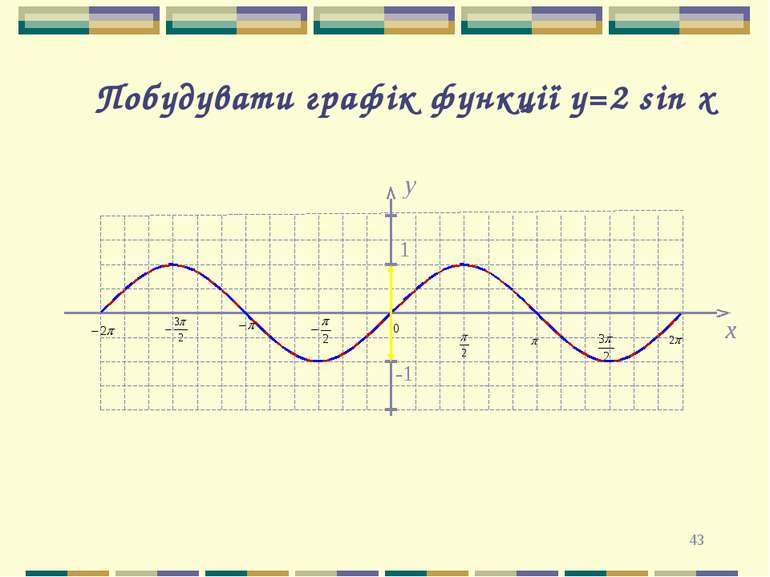
* Перетворення графіків функцій Графік функції y = k f(x) можна дістати з графіка функції y = f(x) за допомогою розтягу його в k разів від осі OX, якщо k>1, і за допомогою стиснення в k разів до осі OX, якщо 0

* y 1 -1 x Побудувати графік функції y=2 sin x

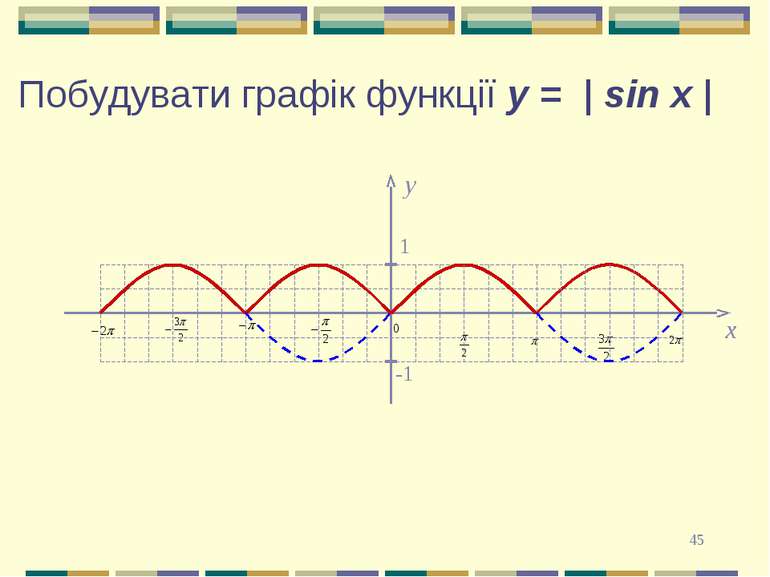
* Перетворення графіків функцій 5. Для побудови графіка функції y =| f(x) | необхідно побудувати графік функції y = f(x) при x≥0, а для x

* y 1 -1 x Побудувати графік функції y = | sin x |

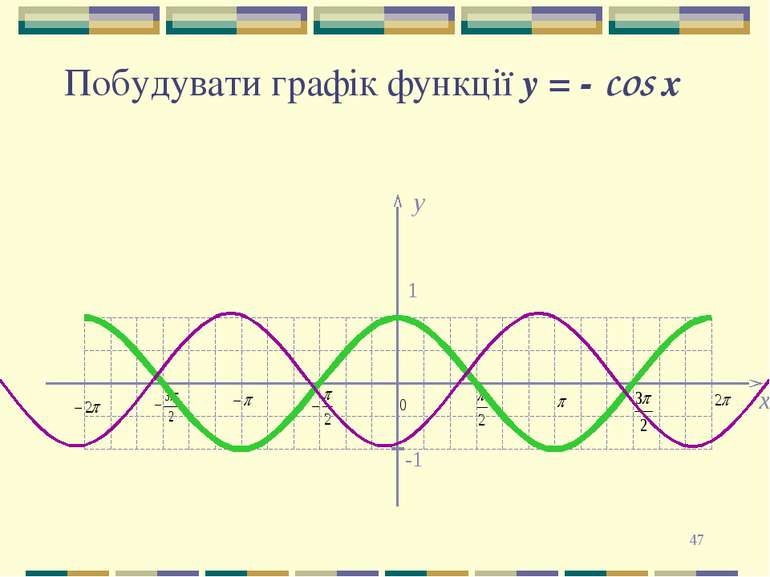
* Перетворення графіків функцій Для побудови графіка функції y = - f(x) необхідно графік функції y = f(x) відобразити симетрично відносно осі OX. Для побудови графіка функції y = f(-x) необхідно графік функції y = f(x) відобразити симетрично відносно осі OY.

* Побудувати графік функції y = - сos x

* Побудувати графік функції y = сtg (x - p/4)

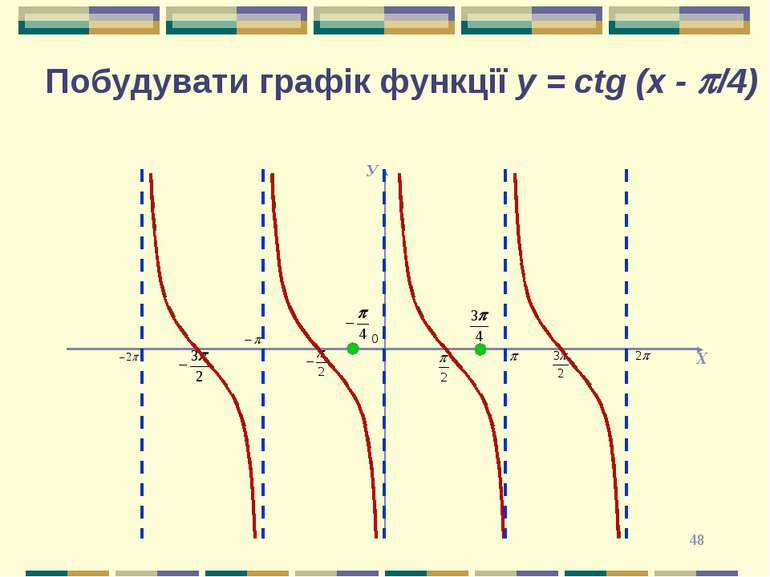
* Запиши функцію Графік функція y=сtgx паралельно перенесли на 4 одиниці вниз вздовж осі Oy і на π/4 одиниці вліво вздовж осі Ox. Отримали наступний графік функції:

* Гармонічні коливання У природі і техніці, повсякденному житті часто доводиться спостерігати коливальні рухи. Наприклад, рух маятника годинника, коливання струни музичного інструмента, коливання води від кинутого в неї предмета та ін До найпростіших коливальних рухів належать гармонічні коливання. Такі коливання можна описати за допомогою тригонометричних функцій (математичною моделлю таких коливань є тригонометричні функції певного виду)

* Гармонічні коливання - це ... Гармонічними коливаннями називаються періодичні коливання фізичної величини, які відбуваються згідно із законом у = у0 cos (ωt + φ0). де t — час,  y0 — це найбільше значення, яке приймає величина y під час коливань, яке називають амплітудою коливань,  ω — циклічна частота коливань, ωt + φ0  —фаза коливань, φ0 називают початковою фазою.

* Уявлення про коливання… Математичний маятник.\ Вільні коливання Графіки координати x(t), швидкості υ(t) і прискоренняa(t) тіла, яке гармонічно коливається. Найпростішою електричною системою,яка викрнує вільні коливання є послідовний RLC-контур

* Приклади застосування Гармонічні коливання дуже розповсюджені в природі й техніці. До них належать малі коливання підвішеного на пружині тягаря, малі коливання маятника, коливання в молекулах, якими зумовлене поглинання інфрачервоних променів, різноманітні коливання в електротехніці, наприклад, у коливальному контурі та інші.

* Тригонометричні функціі — математичні функціі від кута. Вони важливі при вивченні геометрії, а також при дослідженні періодичних процесів. Зазвичай тригонометричні функції визначають як відношення сторін прямокутного трикугника або довжини визначених відрізків в одиничному колі. Більш сучасніші визначення визначають тригонометричні функції через суми рядів або як розв′язки деяких диференціальных рівнянь, що дозволяє поширити область визначення цих функцій на довільні дійсні числа і навіть на комплексні числа.

* Практичне застосування тригонометричних функцій Медицина Телеграф Будівництво Фізика Техніка Астрономія… Проекція на лощину гвинтової лінії свердла також буде синусоїдою.

* Що саме ти не вивчив би, - Ти навчаєшся для себе. Гай Петроній