Презентація на тему:
Поверхні другого порядку

Поверхні другого порядку І частина ЕТ-153 (сфера, конус, еліпсоїд)

До поверхонь другого порядку належать наступні поверхні: Сфера Еліпсоїд Конус

Історія Першу інформацію щодо властивостей геометричних тіл люди знайшли спостерігаючи навколишній світ і в результаті практичної діяльності. З часом вчені відзначили, що деякі властивості геометричних тіл можна отримати з інших властивостей шляхом міркування. Так виникли теореми і доведення. Вчені, які займалися вивченням властивостей поверхонь 2 порядку Евклід Евдокс Кнідзкій Архімед Аполлоній Пергинський

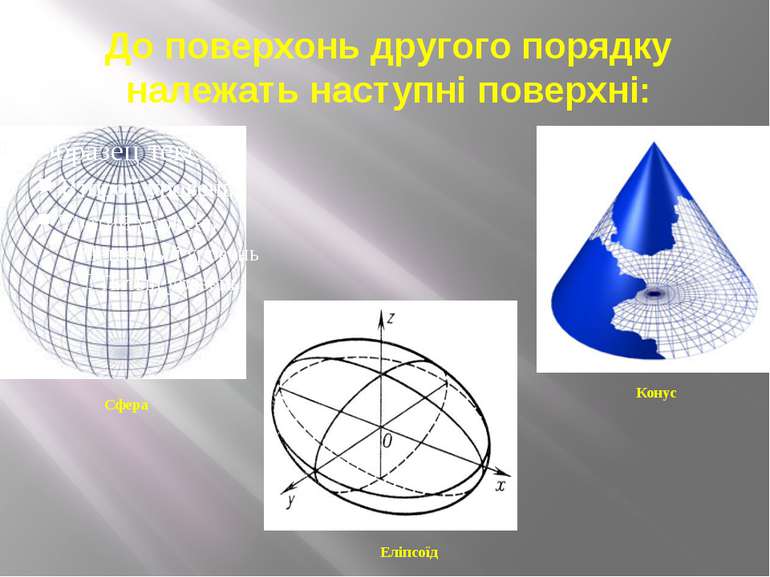
Сфера Сфера (греч. σφαῖρα - куля) - замкнута поверхня, є тілом обертання, яке утворене обертанням півкола навколо свого діаметру. Рівняння де (x0 ,y0,z0)-координати центру сфери, R-її радіус. Основні геометричні формули Площа сфери r-радіус Об'єм кулі, що обмежена сферою r-радіус Площа сегмента сфери H-висота сегмента; θ - зенітний кут (x − x0)2 + (y − y0)2 + (z − z0)2 = R2

Геометрія на сфері Коло, що лежить на сфері, центр якої співпадає з центром сфери, називається великим кругом (великим колом) сфери. Відстань між двома точками на сфері Якщо дані сферичні координати двох точок, то відстань між ними можна знайти так: θ1 і θ2 -широта φ1 і φ2 -довгота

Життєві приклади Найелементарнішим прикладом сфери – це форма нашої планети Земля. Розваги на воді. Повітряна куля. Цікава задумка архітекторів. Кафе «Дзеркальна сфера» в Новосибірську.

Конус Конусом (точніше, круговим конусом) називається тіло, яке складається з круга — основи конуса, точки, що не лежить в площині цього круга- вершини конуса і всіх відрізків, що сполучають вершину конуса з точками основи.

Основні формули конуса Об'єм конуса R-радіус основи; H-висота Площа бічної поверхні конуса R-радіус основи; l-довжина твірної Кут при вершині прямого конуса -кут між двома протилежними твірними α

Використання форми конуса Вафельні стаканчики для морозива. Дорожній конус використовується як обгороження при автомобільному русі

Еліпсоїд Еліпсоїд — замкнута центральна поверхня другого порядку. Еліпсоїд має центр симетрії та три осі, які називаються осями еліпсоїда. Точки перетину координатних осей з еліпсоїдом називаються його вершинами. Рівняння Кординати (a;b;c) – називаються напіосями еліпсоїда

Основні формули еліпсоїда Площа поверхні: Для стислого еліпсоїда Об'єм

Використання форми еліпса М’ячик для гандболу