Презентація на тему:
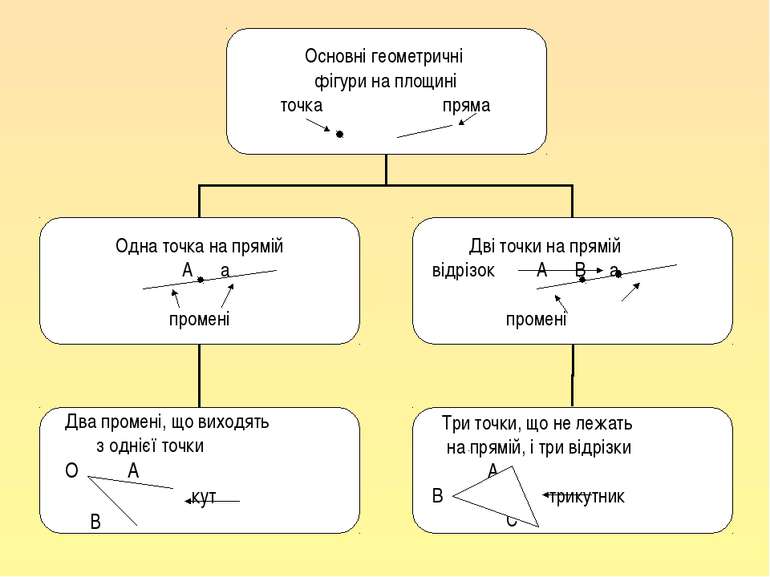
Поняття про трикутник і його елементи

Трикутник і його елементи

засвоїти змісту означення, назв елементів та властивості сторін трикутника (нерівності трикутника); виробити уміння: відтворювати означення трикутника та нерівність трикутника, на готовому рисунку розпізнавати трикутники та називати їх елементи, виконувати зображення трикутника за даною умовою, а також записувати нерівність трикутника для заданого трикутника і використовувати цей запис при розв'язуванні задач; розвивати логічне мислення, сприяти формуванню та розвитку інтелектуальних і творчих здібностей учнів, прищеплювати інтерес до математики; продовжити формувати науковий світогляд і раціональне математичне мислення, виховання працьовитості, позитивне ставлення до навчання і відповідальність за свої досягнення, наполегливості в подоланні труднощів.

1.Яку міру має кут, суміжний із кутом 100˚? а)100˚; б)80˚; в)8˚; г)50˚. 2.Яким є кут, суміжний із тупим кутом? а)тупий; б) прямий; в)гострий; г) розгорнутий. 3. < АОР і

схема

усні вправи

малюнок

малюнок

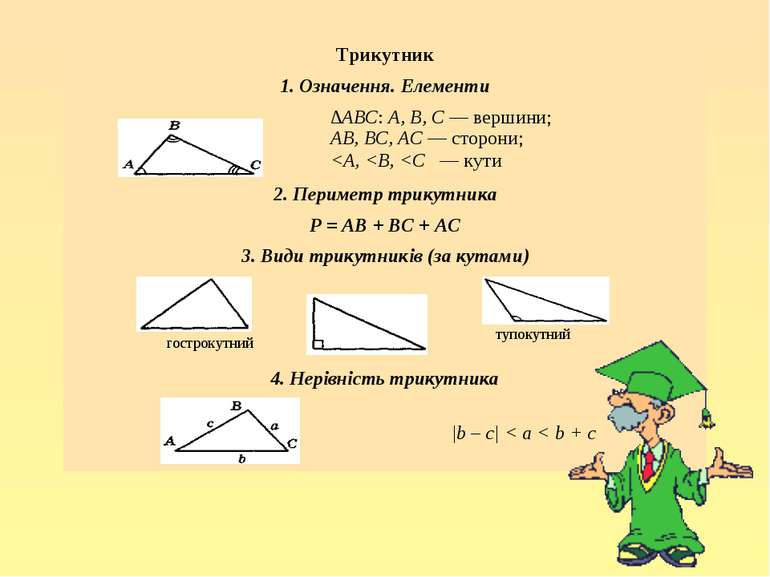
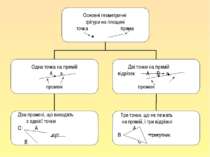
∆АВС: А, В, С — вершини; АВ, ВС, АС — сторони; A, B, Трикутник 1. Означення. Елементи ∆АВС: А, В, С — вершини; АВ, ВС, АС — сторони;

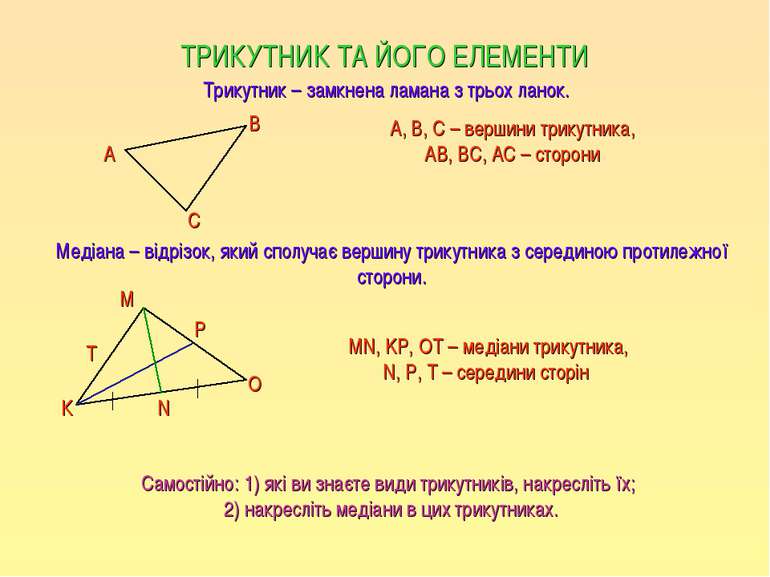
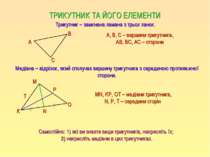
ТРИКУТНИК ТА ЙОГО ЕЛЕМЕНТИ Трикутник – замкнена ламана з трьох ланок. Медіана – відрізок, який сполучає вершину трикутника з серединою протилежної сторони. А В С А, B, С – вершини трикутника, АВ, ВС, АС – сторони К О М T MN, KP, OT – медіани трикутника, N, P, T – середини сторін N P Самостійно: 1) які ви знаєте види трикутників, накресліть їх; 2) накресліть медіани в цих трикутниках.

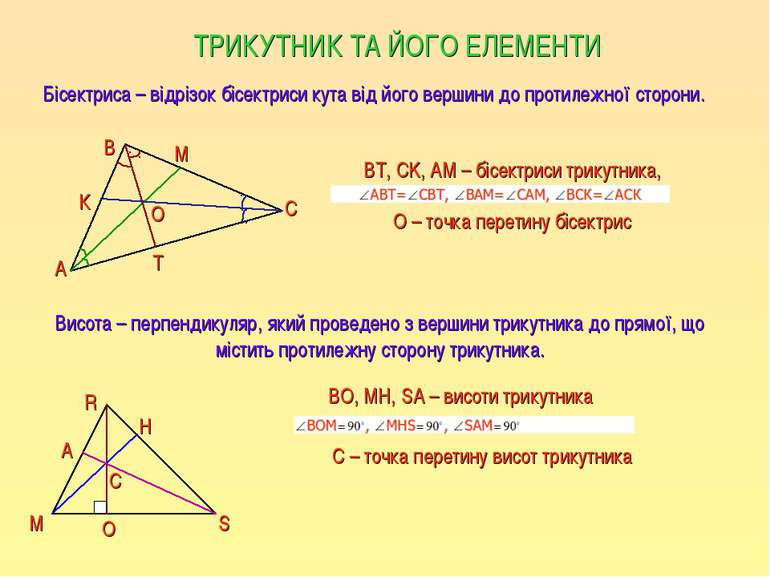
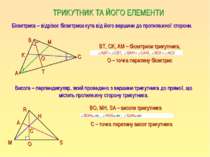
ТРИКУТНИК ТА ЙОГО ЕЛЕМЕНТИ Бісектриса – відрізок бісектриси кута від його вершини до протилежної сторони. М Т А С К В О S ВT, CK, AM – бісектриси трикутника, О – точка перетину бісектрис Висота – перпендикуляр, який проведено з вершини трикутника до прямої, що містить протилежну сторону трикутника. M R С – точка перетину висот трикутника A H O C ВО, МН, SA – висоти трикутника

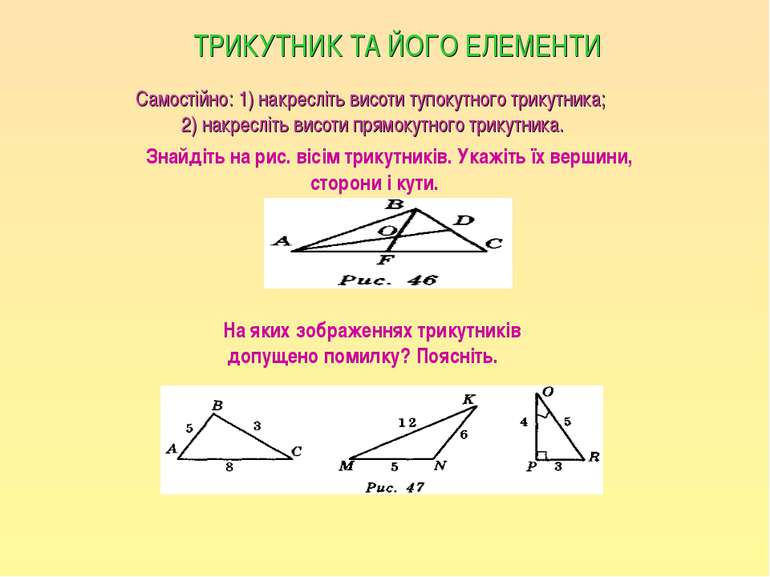
ТРИКУТНИК ТА ЙОГО ЕЛЕМЕНТИ Самостійно: 1) накресліть висоти тупокутного трикутника; 2) накресліть висоти прямокутного трикутника. Знайдіть на рис. вісім трикутників. Укажіть їх вершини, сторони і кути. На яких зображеннях трикутників допущено помилку? Поясніть.

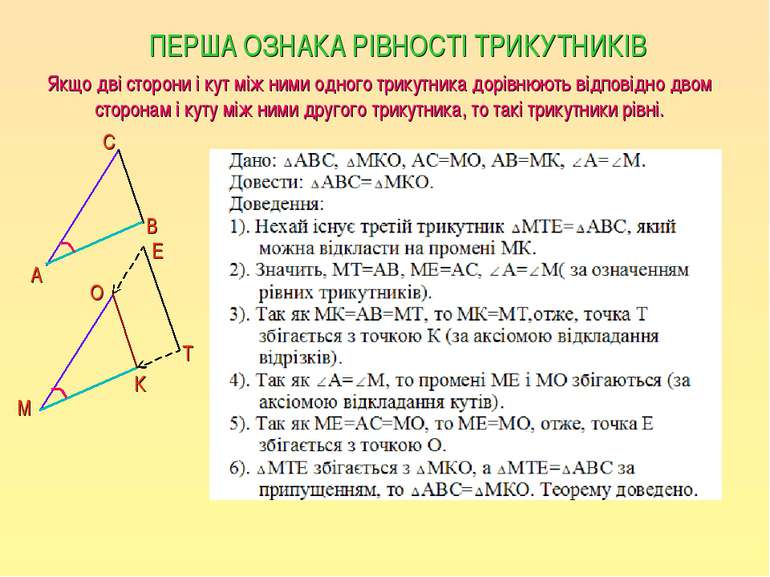
ПЕРША ОЗНАКА РІВНОСТІ ТРИКУТНИКІВ А В С М О К Е Т Якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні.

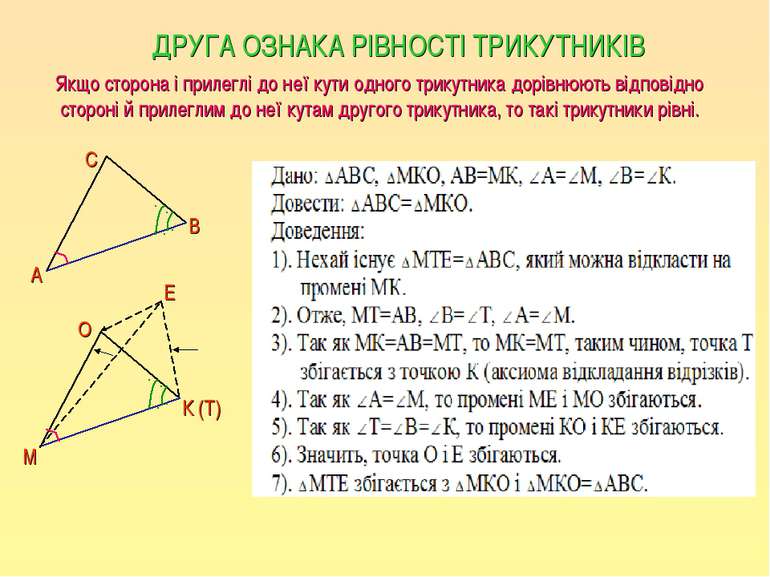
ДРУГА ОЗНАКА РІВНОСТІ ТРИКУТНИКІВ Якщо сторона і прилеглі до неї кути одного трикутника дорівнюють відповідно стороні й прилеглим до неї кутам другого трикутника, то такі трикутники рівні. А С В О К М (Т) Е

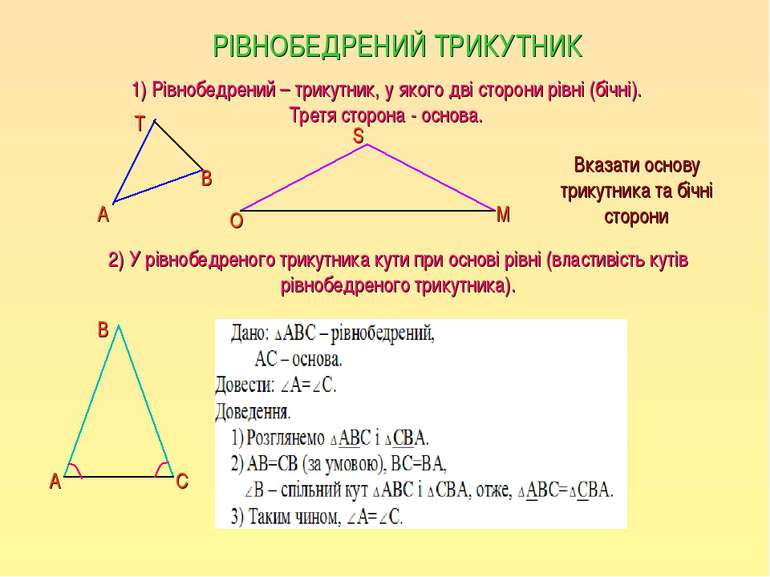
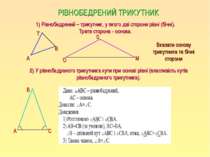
РІВНОБЕДРЕНИЙ ТРИКУТНИК 1) Рівнобедрений – трикутник, у якого дві сторони рівні (бічні). Третя сторона - основа. 2) У рівнобедреного трикутника кути при основі рівні (властивість кутів рівнобедреного трикутника). А Т В О S M Вказати основу трикутника та бічні сторони А В С

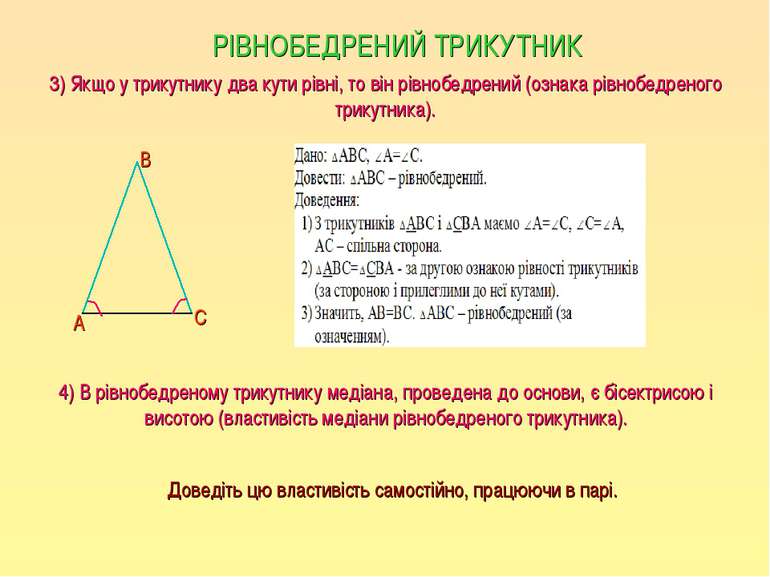
3) Якщо у трикутнику два кути рівні, то він рівнобедрений (ознака рівнобедреного трикутника). РІВНОБЕДРЕНИЙ ТРИКУТНИК А С В 4) В рівнобедреному трикутнику медіана, проведена до основи, є бісектрисою і висотою (властивість медіани рівнобедреного трикутника). Доведіть цю властивість самостійно, працюючи в парі.

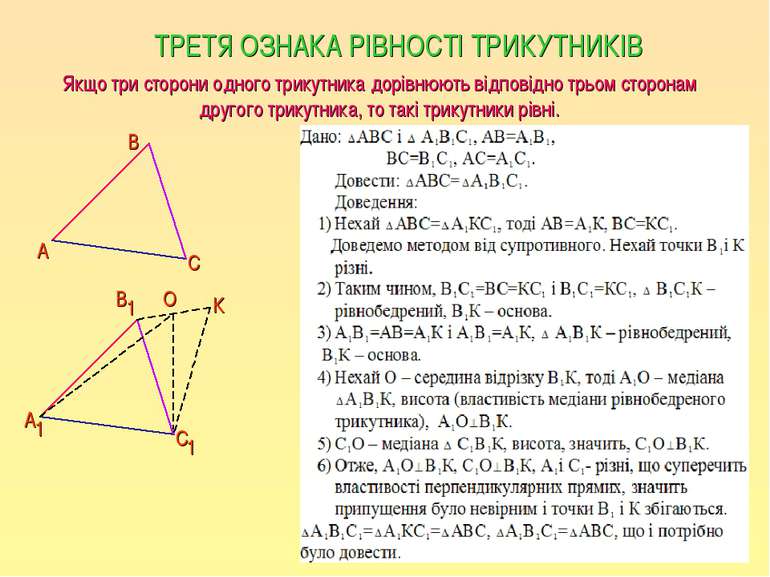
ТРЕТЯ ОЗНАКА РІВНОСТІ ТРИКУТНИКІВ Якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам другого трикутника, то такі трикутники рівні. А В С 1 А В С О 1 1 К

ВЛАСТИВОСТІ ТРИКУТНИКІВ 1) У рівносторонньому трикутнику градусні міри всіх кутів дорівнюють 60 . о 2) У рівносторонньому трикутнику будь-яка медіана є бісектрисою та висотою. 3) У кожному трикутнику проти більшої сторони лежить більший кут. 4) Кожна сторона трикутника менша від суми двох інших його сторін. РОБОТА У ПАРАХ. ПРОБЛЕМНІ ПИТАННЯ. Чи буде вірним твердження : “Якщо дві сторони і кут не між ними одного трикутника дорівнюють відповідно двом сторонам і куту не між ними другого трикутника, то такі трикутники рівні” ? (Обгрунтуйте відповідь).

1. Дано дві точки. Як треба вибрати на площині третю точку, щоб усі три точки разом могли бути вершинами деякого трикутника? 2. Як називатиметься тоді величина, що дорівнює сумі відстаней між цими точками, взятих попарно? 3. Чи існує трикутник зі сторонами, довжини яких пропорційні числам 2, 3, 4?

§ 9, с. 76, 77 — вивчити означення та властивості сторін трикутника. Письмові вправи. 1) Периметр трикутника ABC дорівнює 24 м, причому АВ = 10 м, а сторона ВС втричі менша, ніж сторона АС. Знайдіть невідомі сторони трикутника ABC. 2) Периметр трикутника ABC дорівнює 18 см, причому АВ = 6 см. Якими можуть бути довжини двох інших сторін трикутника, якщо вони виражаються цілими числами? 3) № 263, 269, 277. Вправа на повторення. Знайти градусні міри суміжних кутів, якщо вони відносяться як 3:7.