Презентація на тему:
Поняття про подібні трикутники

Черкаська приватна загальноосвітня школа “Софія” вчитель математики Ратушна Аліна Валеріївна

Усім нам часто доводиться мати справу з предметами однакової форми, але різних розмірів. Наприклад: зменшена модель автомобіля схожа на справжній автомобіль. Але їх розміри відповідно пропорційні.

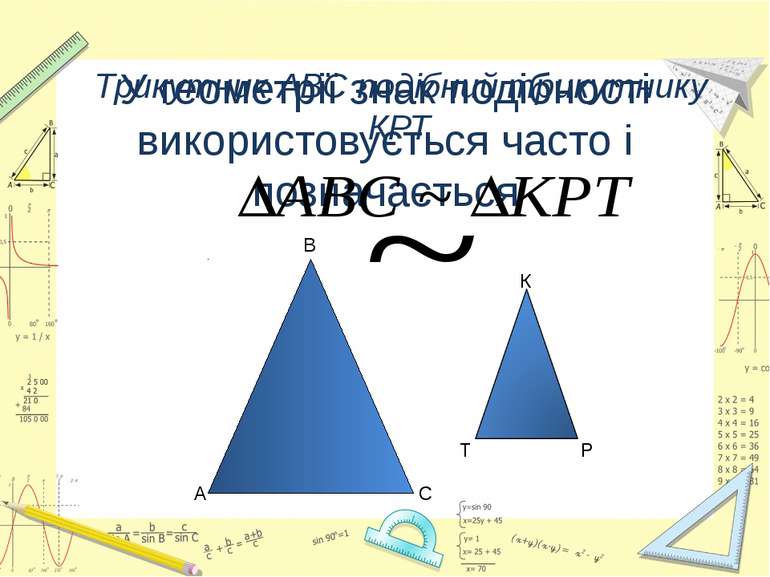
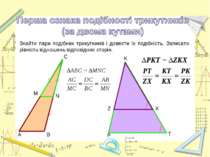
У геометрії знак подібності використовується часто і позначається Трикутник АВС подібний трикутнику КРТ

Подібні трикутники А1 С1 В1 2b 2a 2c Число, якому дорівнює відношення відповідних сторін подібних трикутників, називається коефіцієнтом подібності (позначають k) ΔАВС ~ ΔА 1В 1С 1

Щоб скласти відношення відповідних сторін подібних трикутників, потрібно: визначити відповідно рівні кути трикутника; з'ясувати, які сторони є відповідними; записати рівність трьох дробів, у чисельниках яких – сторони одного з трикутників, а у знаменниках – відповідні сторони іншого А С В А1 С1 В1 Відношення периметрів подібних трикутників дорівнює відношенню їх відповідних сторін.

ФАЛЕС МІЛЕТСЬКИЙ (кін. 624 – кін. 546 до н. е.) «Блаженство тіла – в здоров’ї, блаженство розуму – в знаннях»

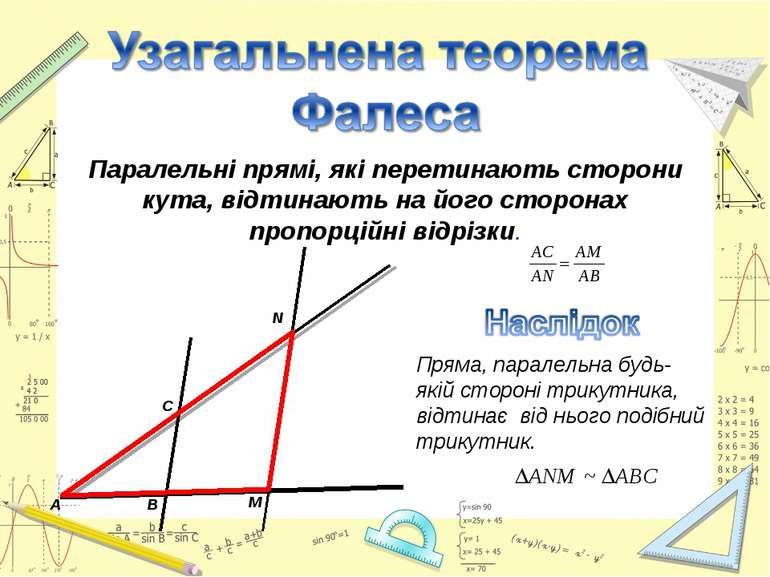
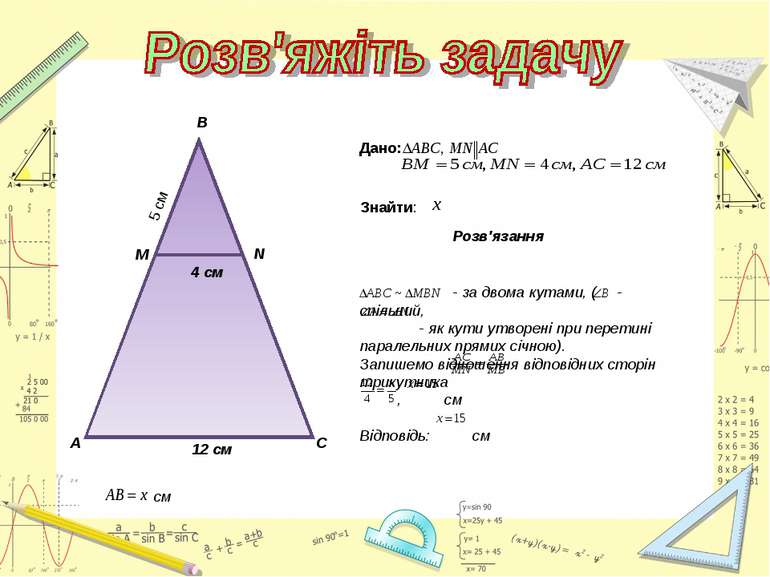
Паралельні прямі, які перетинають сторони кута, відтинають на його сторонах пропорційні відрізки. Пряма, паралельна будь-якій стороні трикутника, відтинає від нього подібний трикутник. А В М N С

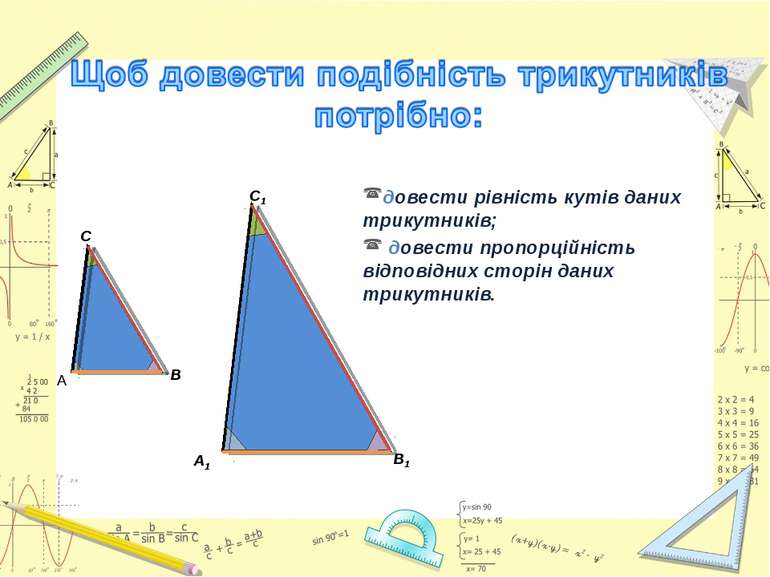
довести рівність кутів даних трикутників; довести пропорційність відповідних сторін даних трикутників. А1 В1 А С В С1

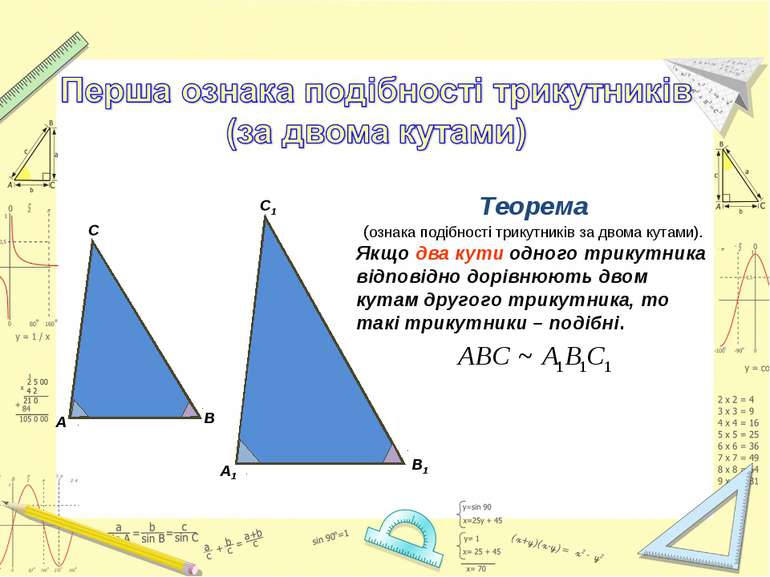
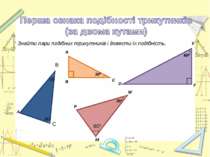
Теорема (ознака подібності трикутників за двома кутами). Якщо два кути одного трикутника відповідно дорівнюють двом кутам другого трикутника, то такі трикутники – подібні. А1 В1 С1

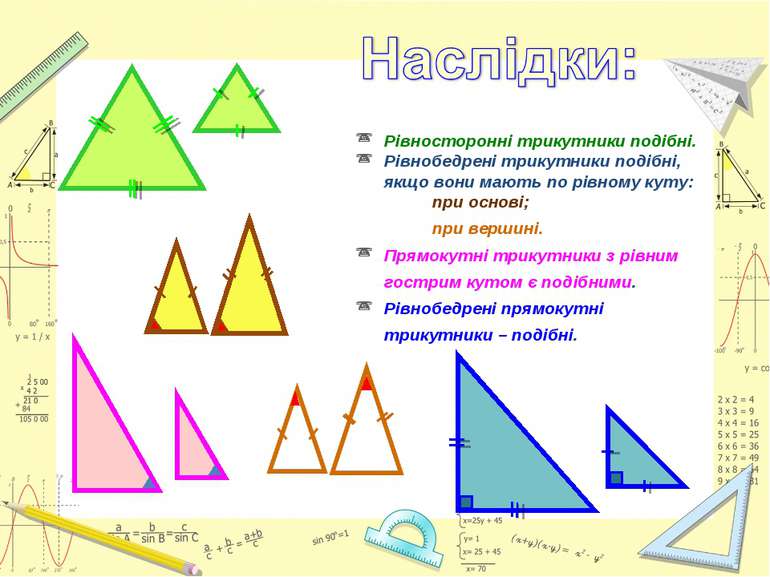
Рівносторонні трикутники подібні. Рівнобедрені трикутники подібні, якщо вони мають по рівному куту: при основі; при вершині. Прямокутні трикутники з рівним гострим кутом є подібними. Рівнобедрені прямокутні трикутники – подібні.

Знайти пари подібних трикутників і довести їх подібність.

Знайти пари подібних трикутників і довести їх подібність.

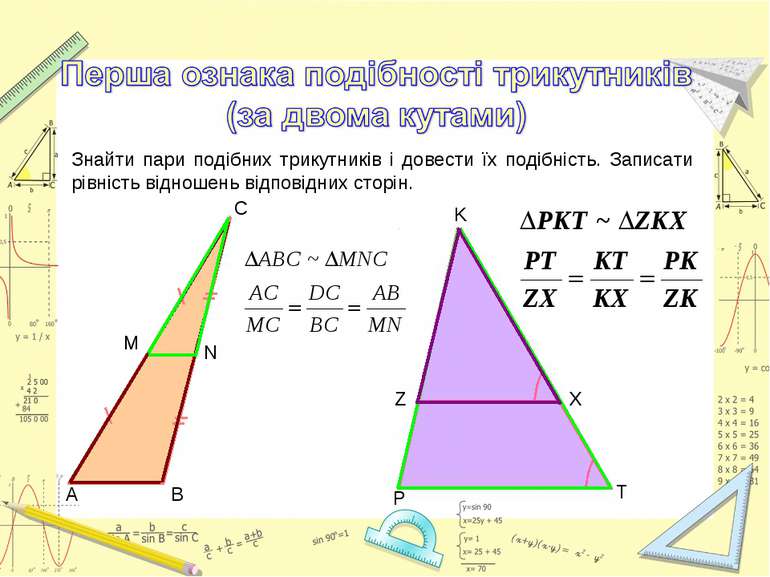
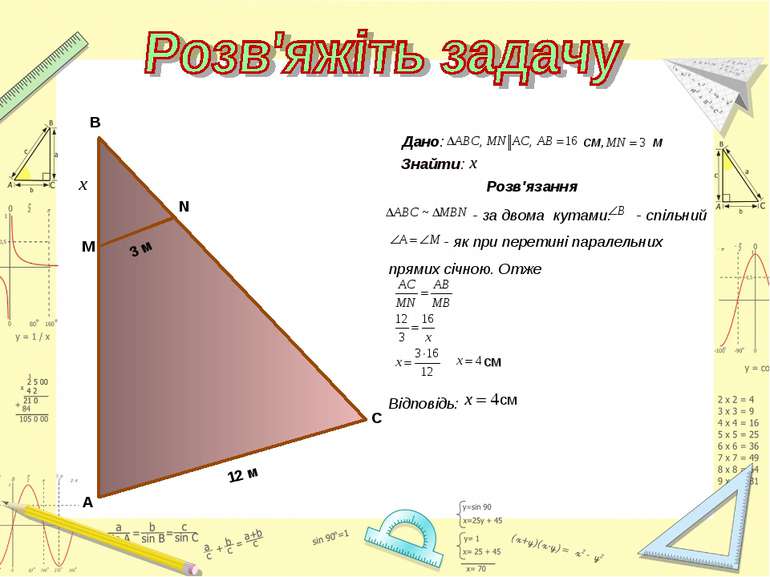
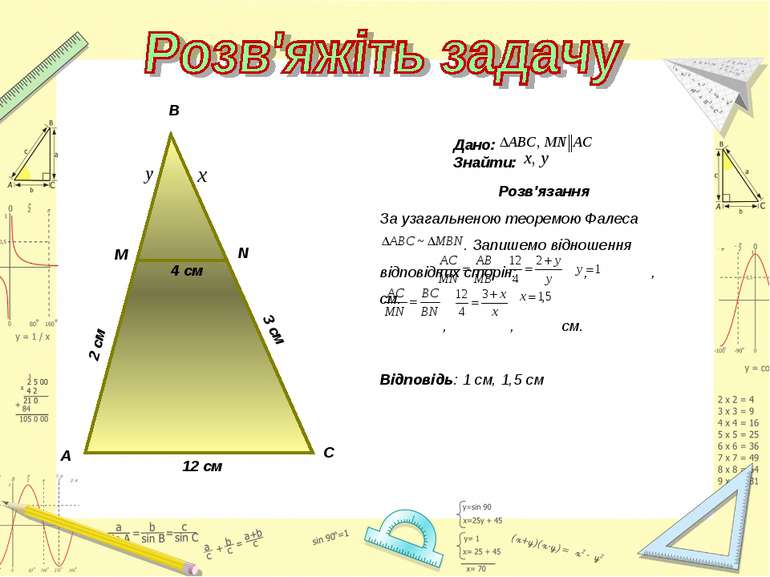
Знайти пари подібних трикутників і довести їх подібність. Записати рівність відношень відповідних сторін. А М В N С

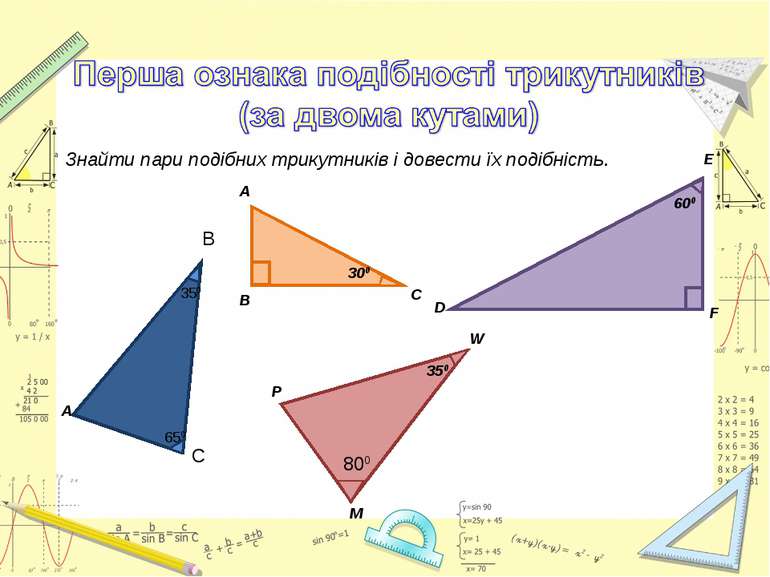
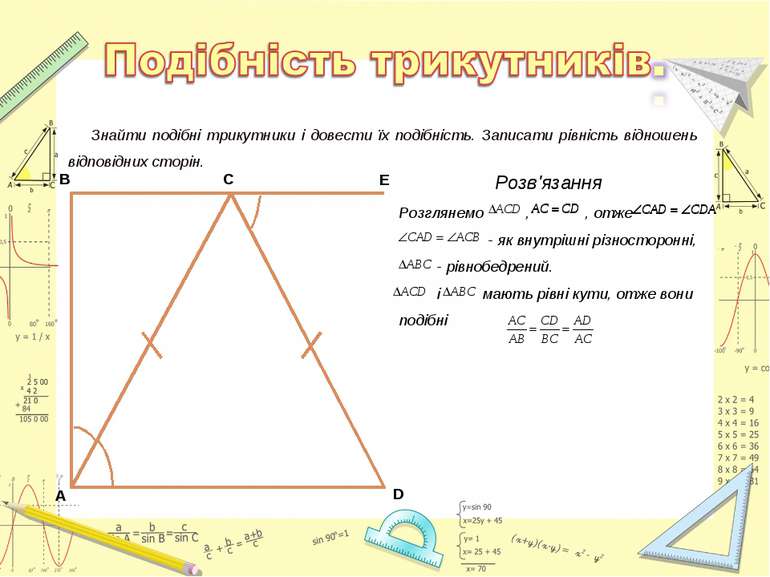
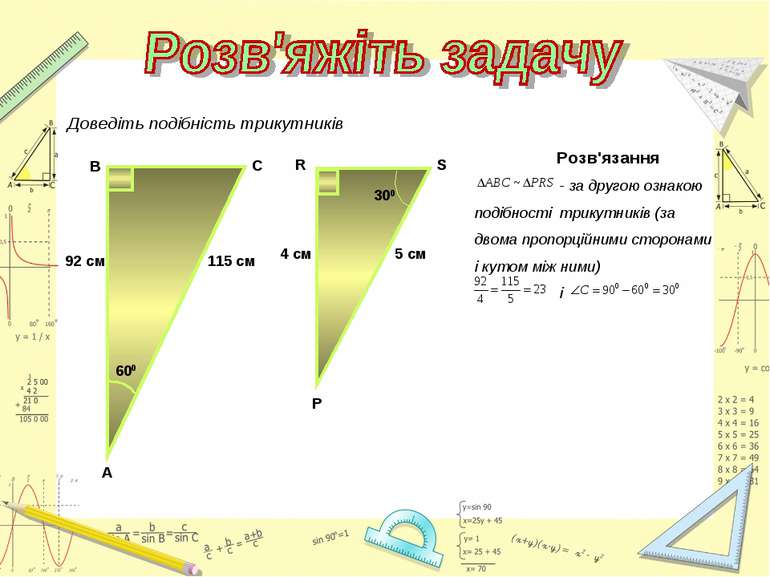
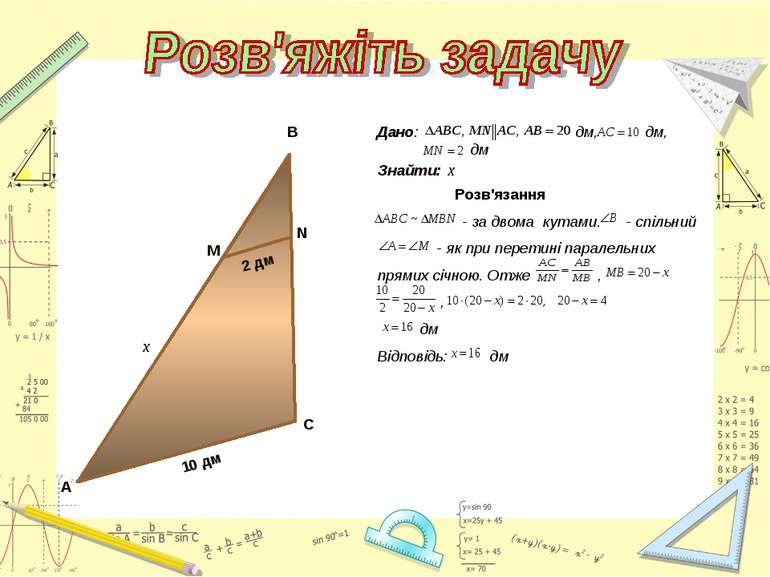
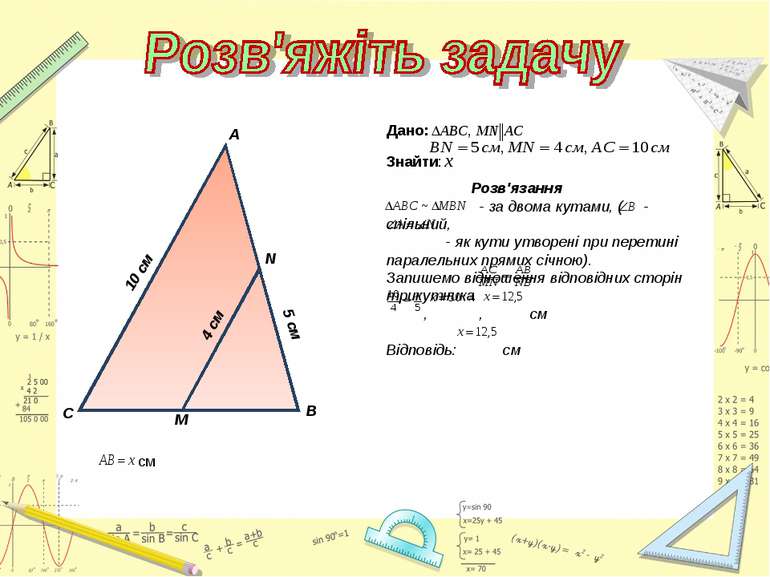
Знайти подібні трикутники і довести їх подібність. Записати рівність відношень відповідних сторін. Розв'язання

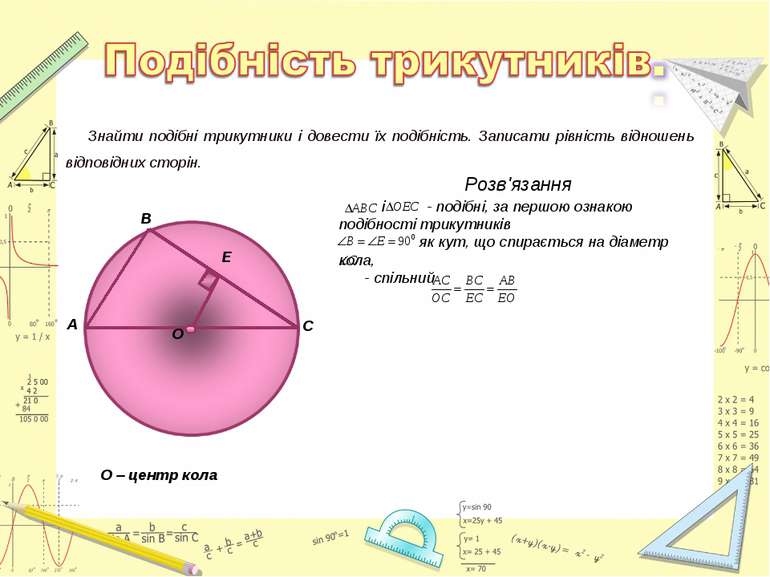
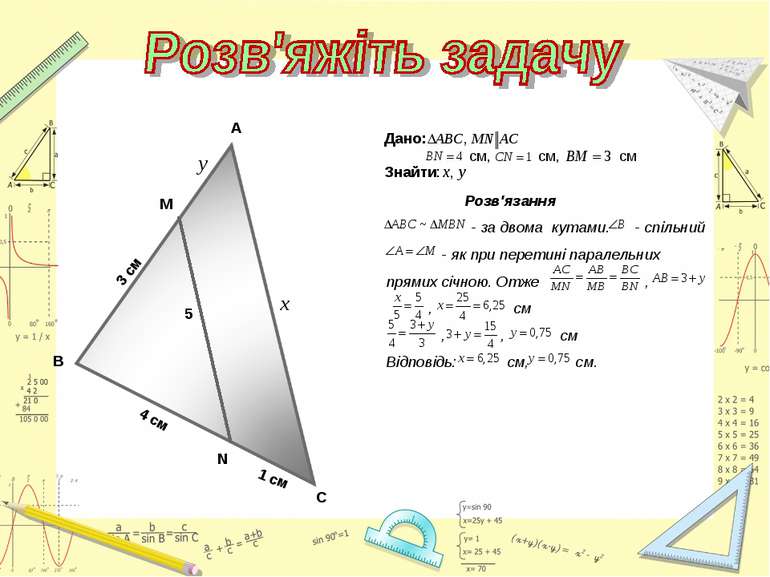
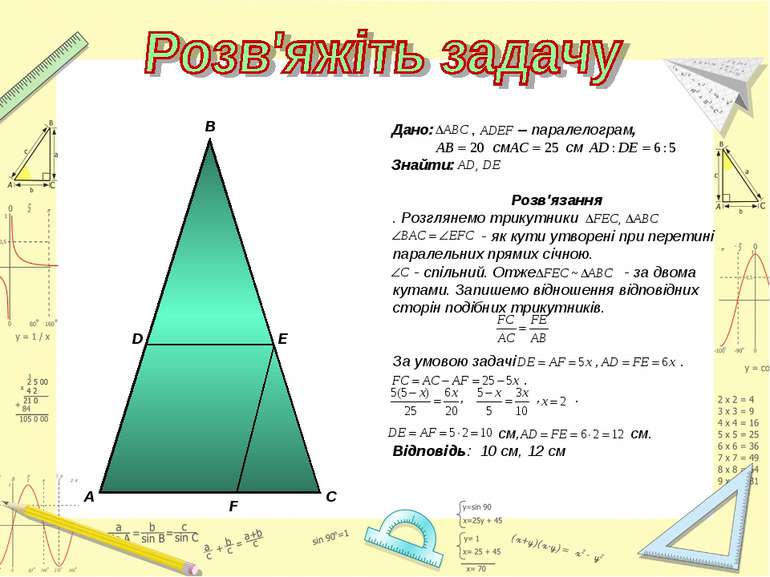
Знайти подібні трикутники і довести їх подібність. Записати рівність відношень відповідних сторін. Розв'язання

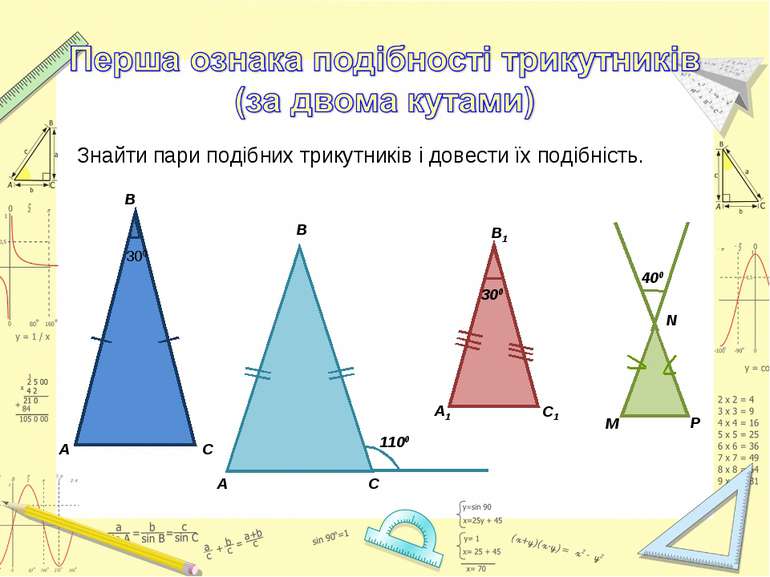
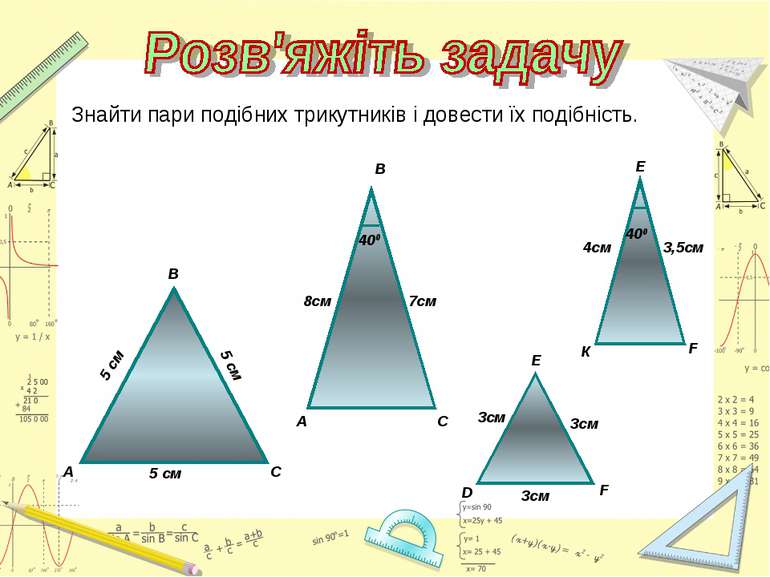
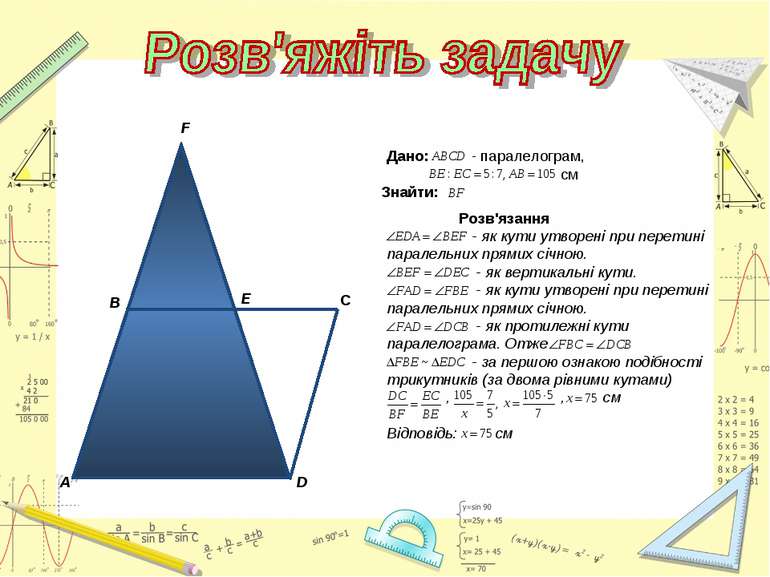
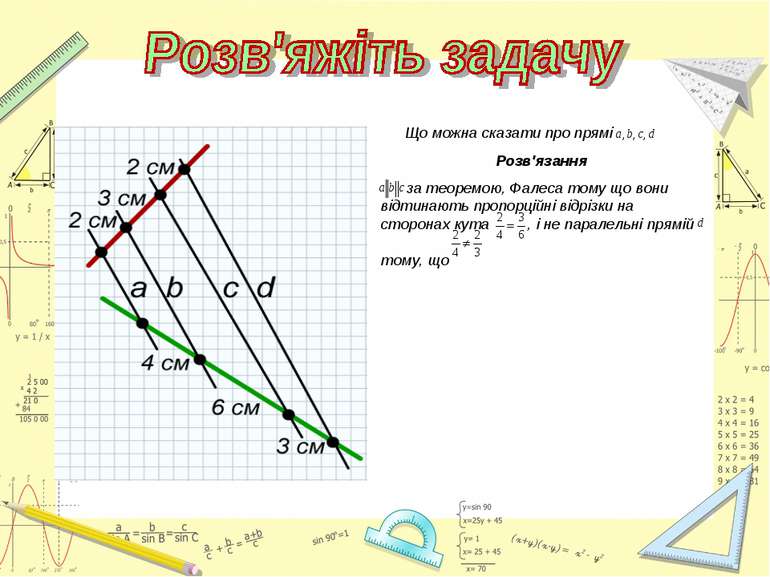
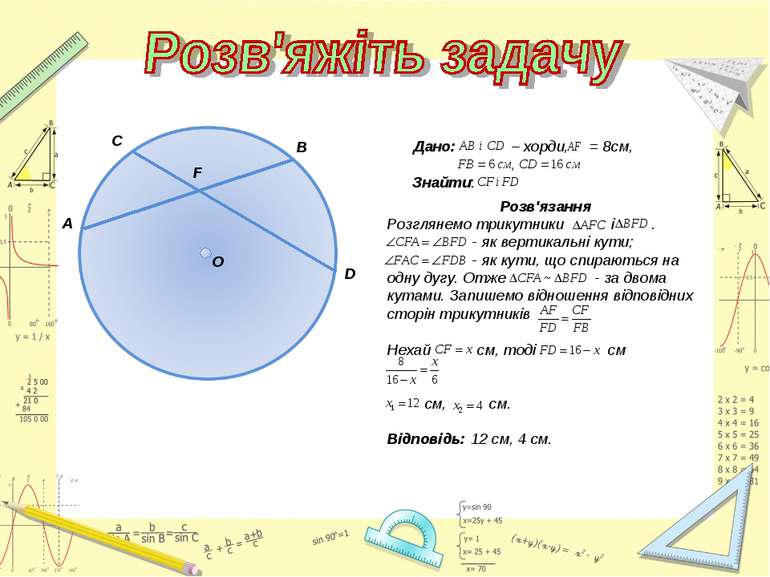
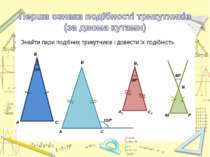
Знайти подібні трикутники і довести їх подібність. Записати рівність відношень відповідних сторін.

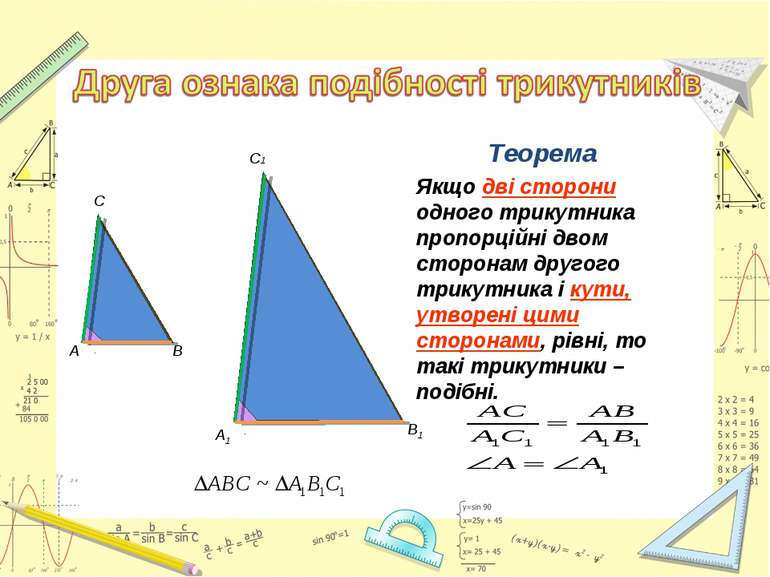
Якщо дві сторони одного трикутника пропорційні двом сторонам другого трикутника і кути, утворені цими сторонами, рівні, то такі трикутники –подібні. А1 В1 А С В С1 Теорема

Знайти пари подібних трикутників і довести їх подібність.

Знайти пари подібних трикутників і довести їх подібність.

Доведіть подібність трикутників Розв'язання

А

Теорема В1 Якщо три сторони одного трикутника пропорційні трьом сторонам другого трикутника, то такі трикутники подібні. А1 А С В С1

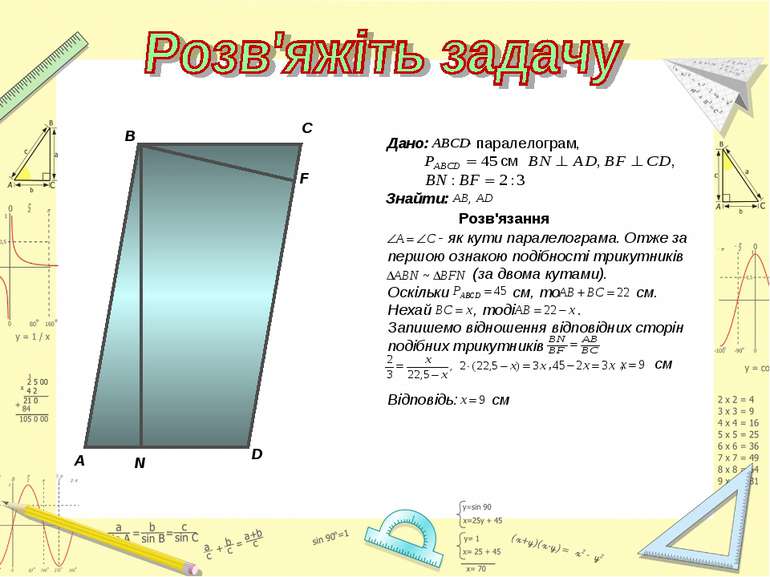
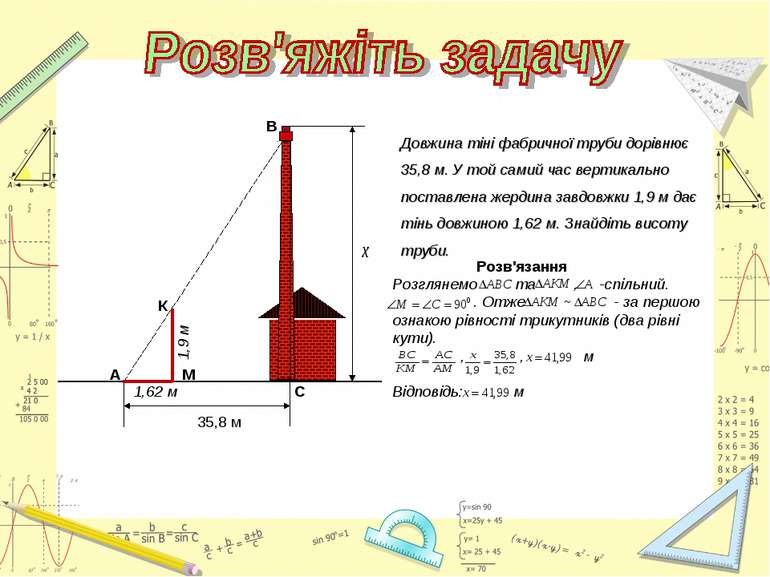
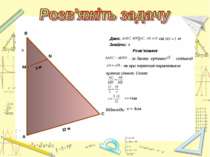
Довжина тіні фабричної труби дорівнює 35,8 м. У той самий час вертикально поставлена жердина завдовжки 1,9 м дає тінь довжиною 1,62 м. Знайдіть висоту труби. А В С К М Розв'язання

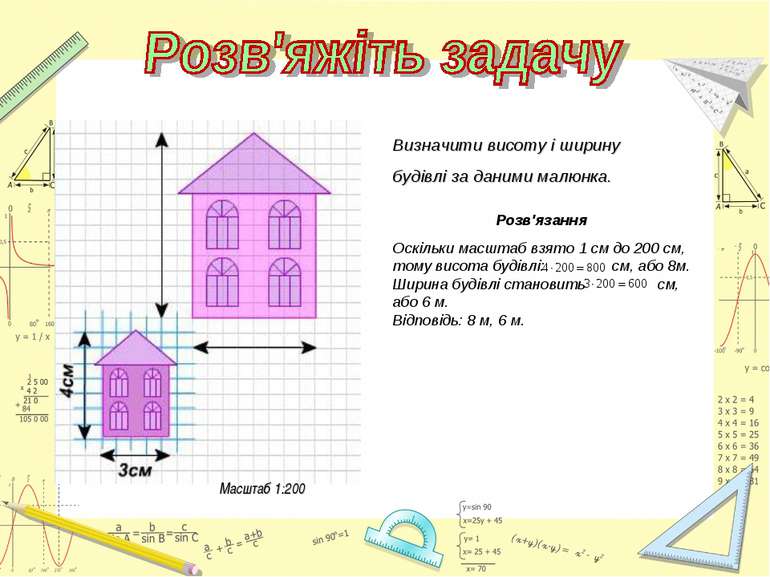
Масштаб 1:200 Визначити висоту і ширину будівлі за даними малюнка. Розв'язання Оскільки масштаб взято 1 см до 200 см, тому висота будівлі: см, або 8м. Ширина будівлі становить см, або 6 м. Відповідь: 8 м, 6 м.

Що можна сказати про прямі Розв'язання

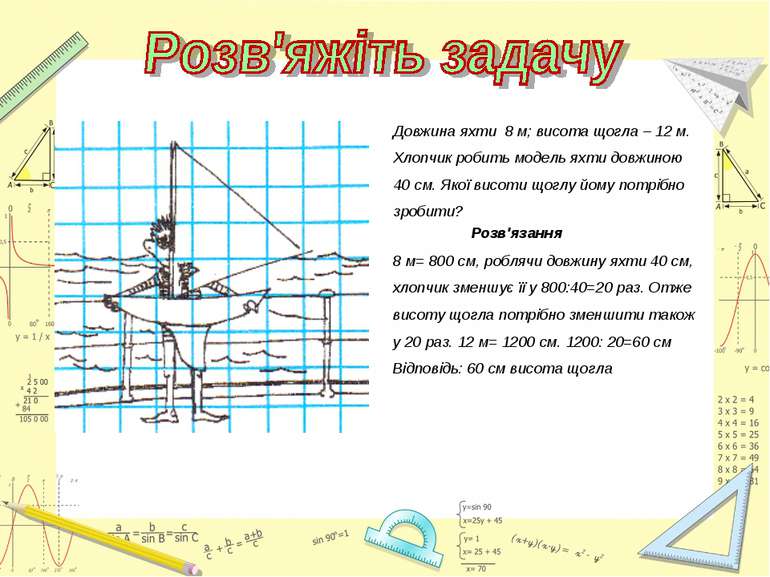
Довжина яхти 8 м; висота щогла – 12 м. Хлопчик робить модель яхти довжиною 40 см. Якої висоти щоглу йому потрібно зробити? Розв'язання 8 м= 800 см, роблячи довжину яхти 40 см, хлопчик зменшує її у 800:40=20 раз. Отже висоту щогла потрібно зменшити також у 20 раз. 12 м= 1200 см. 1200: 20=60 см Відповідь: 60 см висота щогла

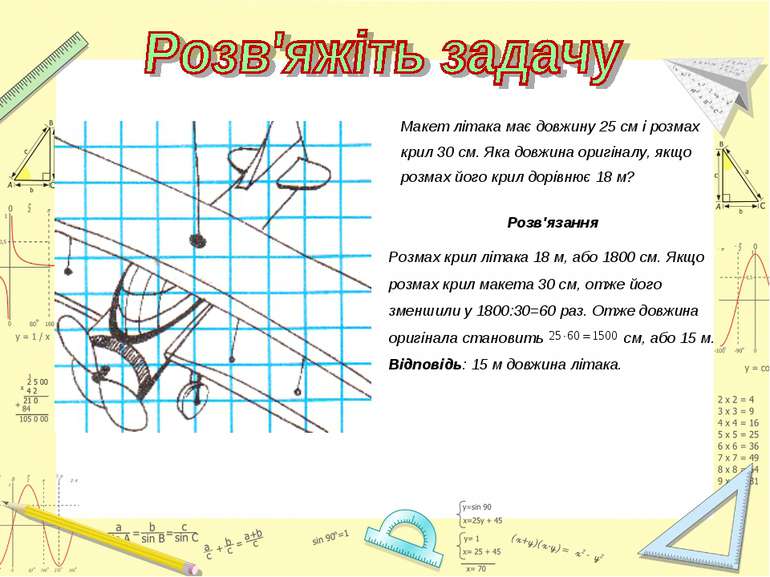
Макет літака має довжину 25 см і розмах крил 30 см. Яка довжина оригіналу, якщо розмах його крил дорівнює 18 м? Розв'язання

Діаметр глобуса дорівнює 40 см; діаметр Землі – 12 000 км. Визначте відстань від Києва до Москви, якщо на глобусі ці міста розділені відстанню 10 см. Розв'язання Визначимо у скільки раз модель глобуса менша за Землю 12 000 км = 1 200 000 000 см 1 200 000 000: 40 = 30 000 000. Отже відстань від Новосибірська до Москви буде у стільки раз більша ніж на глобусі І дорівнює 300 000 000 см = 30 000 км Відповідь: відстань від Києва до Москви 30 000км.

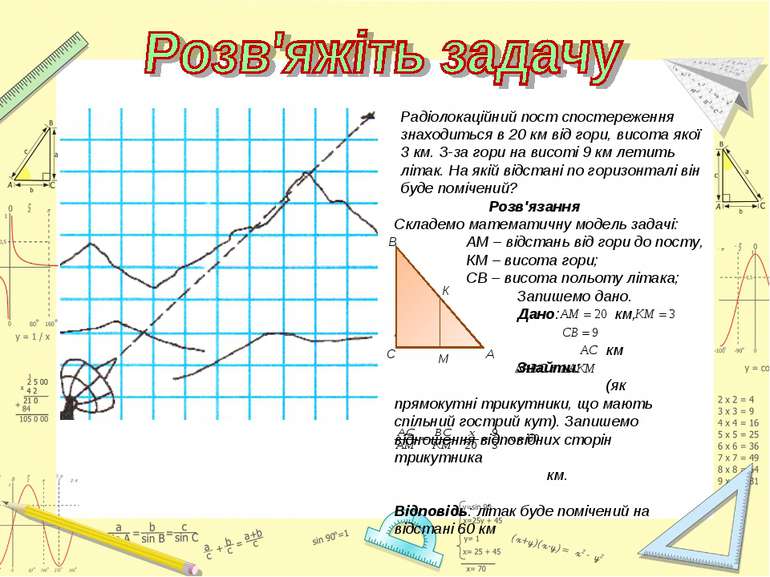
Радіолокаційний пост спостереження знаходиться в 20 км від гори, висота якої 3 км. З-за гори на висоті 9 км летить літак. На якій відстані по горизонталі він буде помічений? Розв'язання

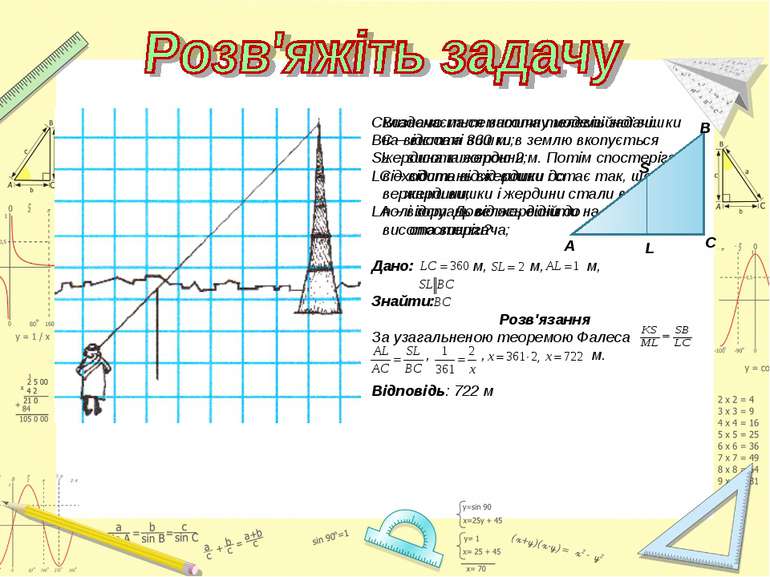
Визначається висота телевізійної вишки на відстані 360 м. в землю вкопується жердина висотою 2 м. Потім спостерігач відходить від жердини і стає так, щоб вершини вишки і жердини стали в одному полі зору. Довелось відійти на 1 м. Яка висота вишки?

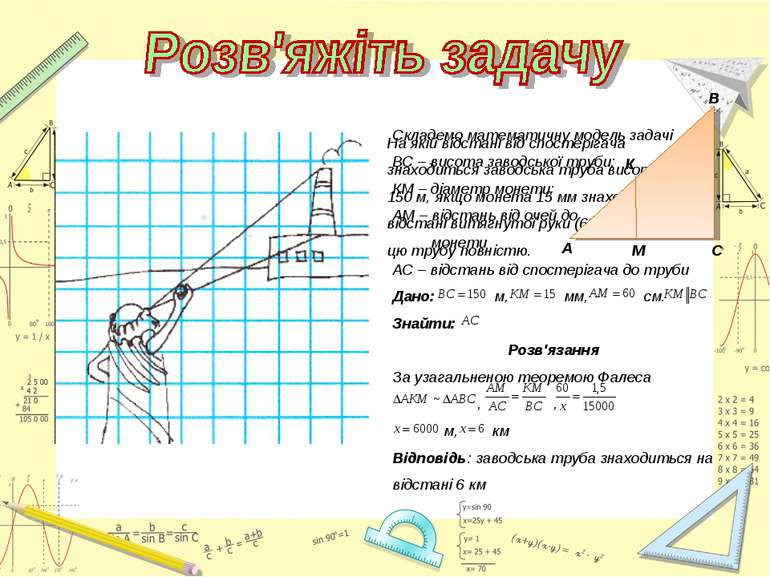
На якій відстані від спостерігача знаходиться заводська труба висотою 150 м, якщо монета 15 мм знаходиться на відстані витягнутої руки (60 см), заслоняє цю трубу повністю.

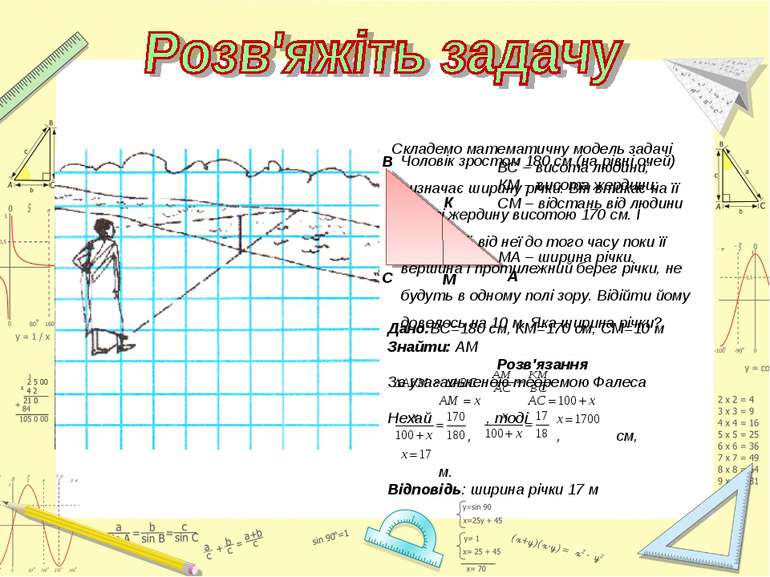
Чоловік зростом 180 см (на рівні очей) визначає ширину річки. Він втикає на її березі жердину висотою 170 см. І відходить від неї до того часу поки її вершина і протилежний берег річки, не будуть в одному полі зору. Відійти йому довелось на 10 м. Яка ширина річки?

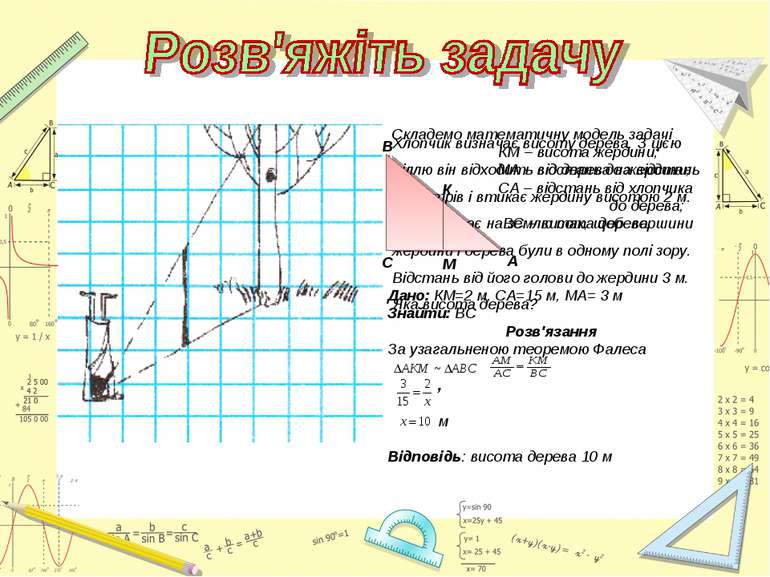
Хлопчик визначає висоту дерева. З цією ціллю він відходить від дерева на відстань 15 метрів і втикає жердину висотою 2 м. Потім лягає на землю так, щоб вершини жердини і дерева були в одному полі зору. Відстань від його голови до жердини 3 м. Яка висота дерева?

Розв'язання

Розв'язання