Презентація на тему:
Побудова кута, що дорівнює даному. Побудова бісектриси кута

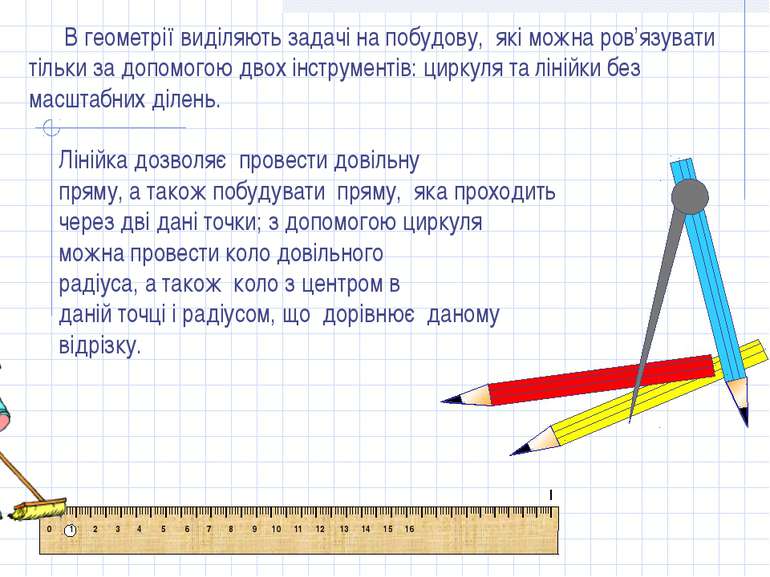
В геометрії виділяють задачі на побудову, які можна ров’язувати тільки за допомогою двох інструментів: циркуля та лінійки без масштабних ділень. Лінійка дозволяє провести довільну пряму, а також побудувати пряму, яка проходить через дві дані точки; з допомогою циркуля можна провести коло довільного радіуса, а також коло з центром в даній точці і радіусом, що дорівнює даному відрізку. IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

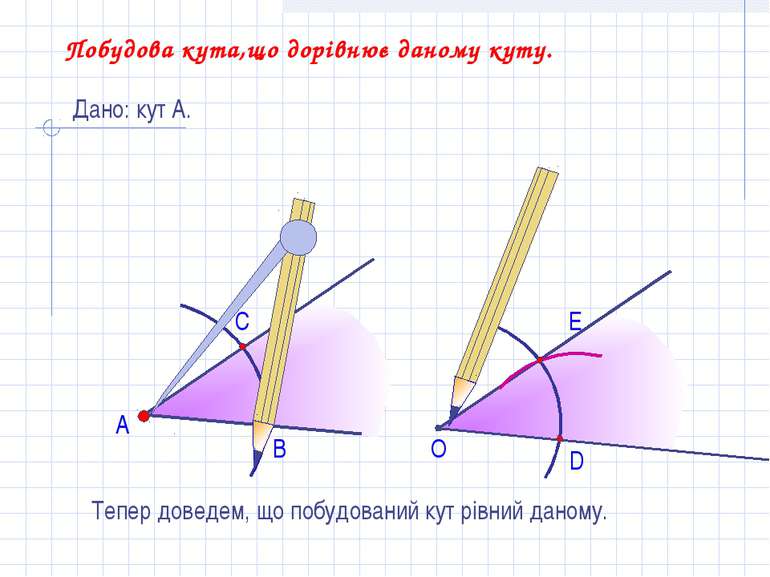
А В С Побудова кута,що дорівнює даному куту. Дано: кут А. О D E Тепер доведем, що побудований кут рівний даному.

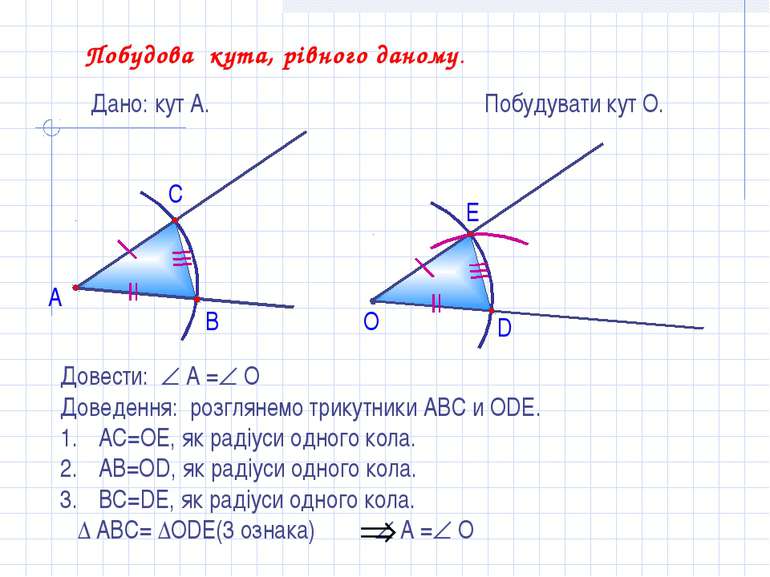
Побудова кута, рівного даному. Дано: кут А. А Побудувати кут О. В С О D E Довести: А = О Доведення: розглянемо трикутники АВС и ОDE. АС=ОЕ, як радіуси одного кола. АВ=ОD, як радіуси одного кола. ВС=DE, як радіуси одного кола. ∆ АВС= ∆ОDЕ(3 ознака) А = О

бісектриса Побудова бісектриси даного кута.

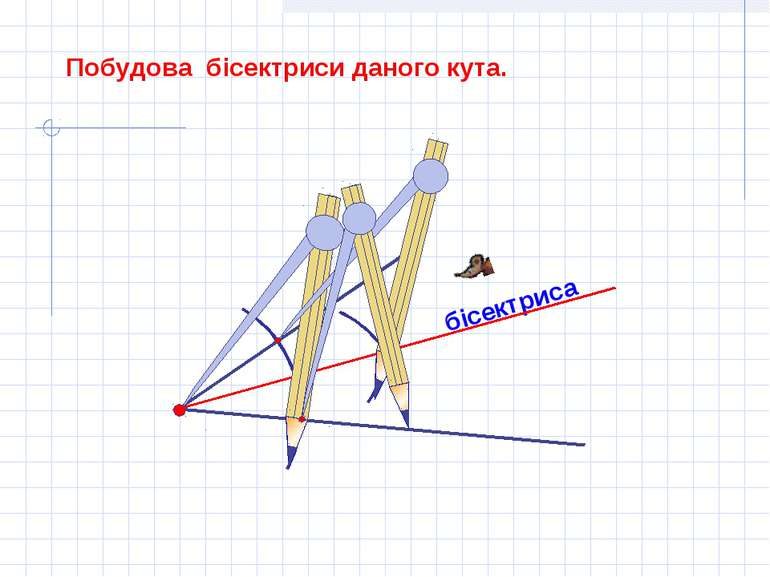
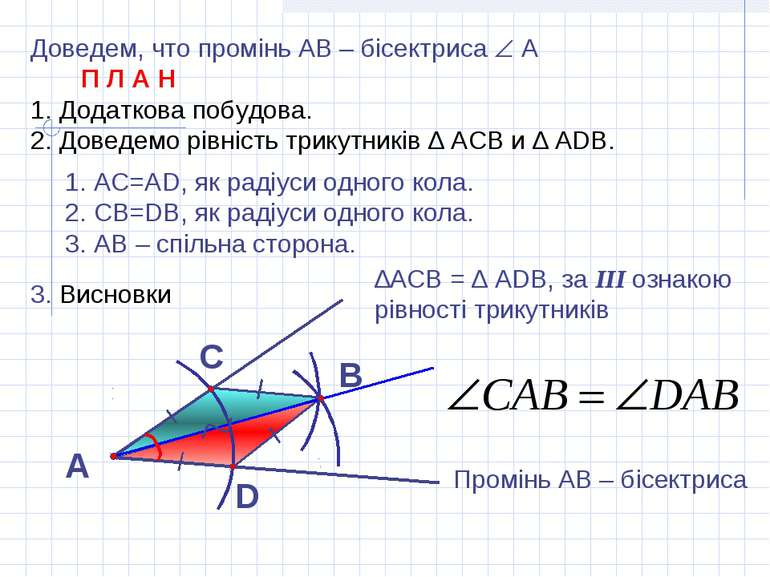
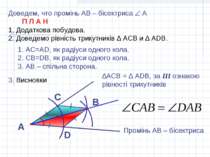
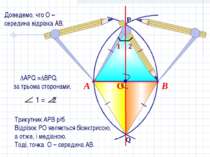
Доведем, что промінь АВ – бісектриса А П Л А Н Додаткова побудова. Доведемо рівність трикутників ∆ АСВ и ∆ АDB. 3. Висновки А В С D АС=АD, як радіуси одного кола. СВ=DB, як радіуси одного кола. АВ – спільна сторона. ∆АСВ = ∆ АDВ, за III ознакою рівності трикутників Промінь АВ – бісектриса

В А Побудова перпендикулярних прямих.

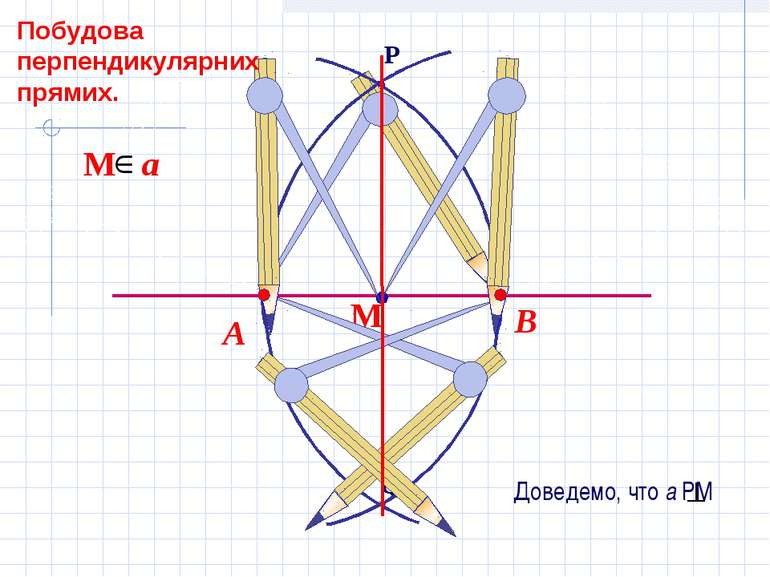
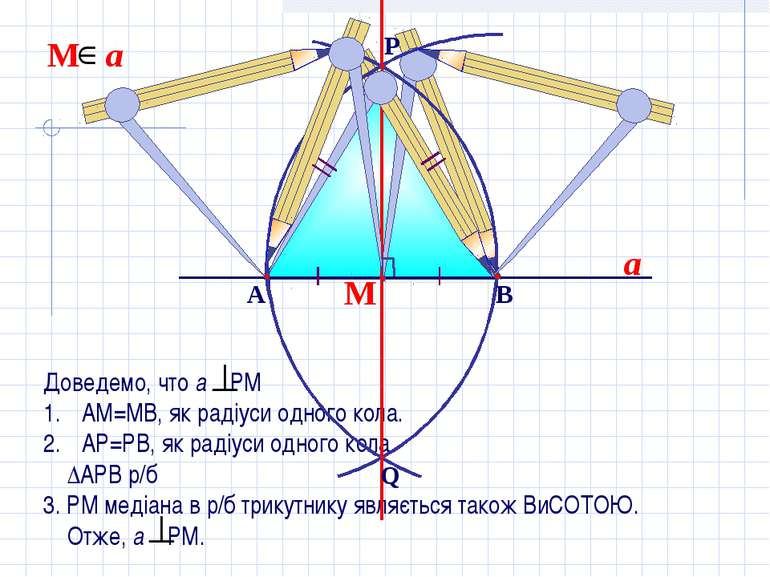
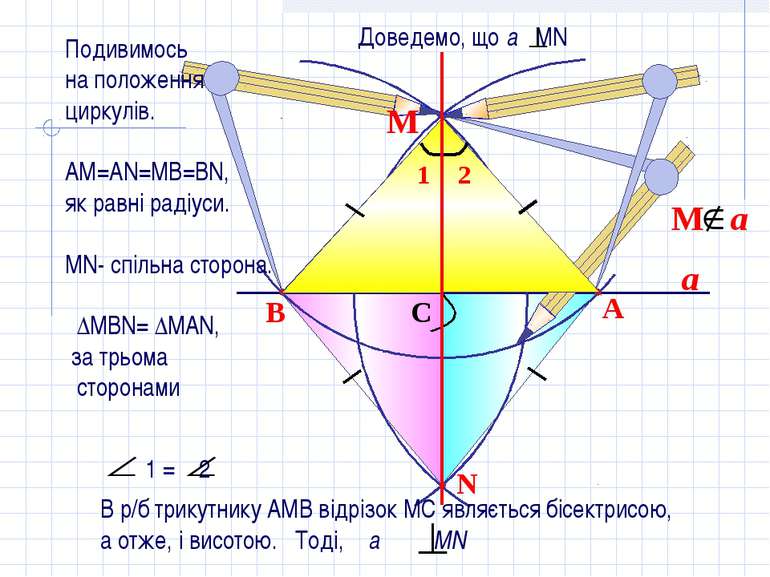
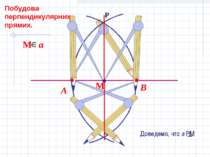
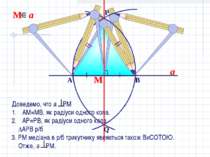
Доведемо, что а РМ АМ=МВ, як радіуси одного кола. АР=РВ, як радіуси одного кола ∆АРВ р/б 3. РМ медіана в р/б трикутнику являється також ВиСОТОЮ. Отже, а РМ. М a

a N М Побудова перпендикулярних прямих.

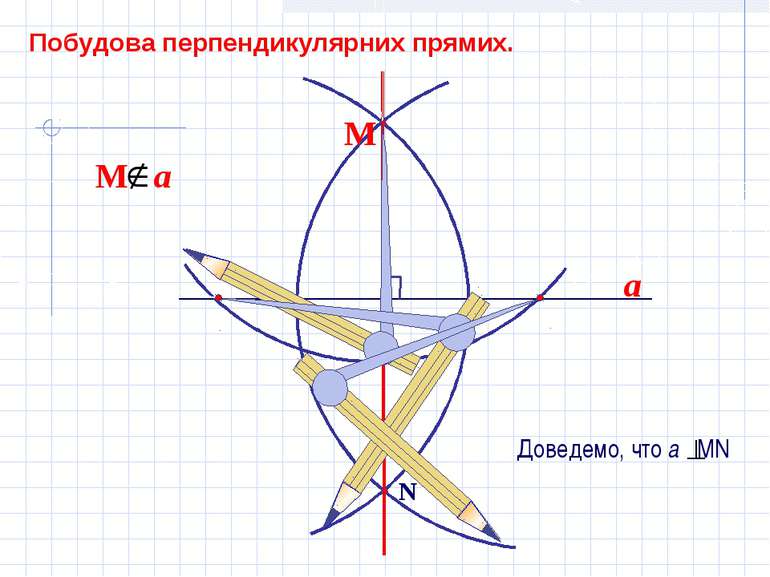
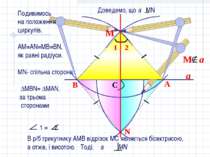
a N B A C М Подивимось на положення циркулів. АМ=АN=MB=BN, як равні радіуси. МN- спільна сторона. ∆MВN= ∆MAN, за трьома сторонами

Доведемо, что О – середина відрізка АВ. Побудова середини відрізка

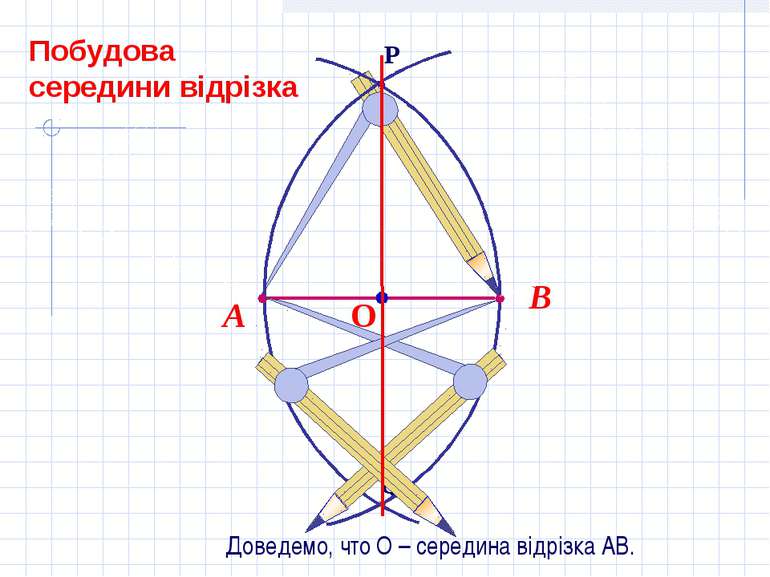
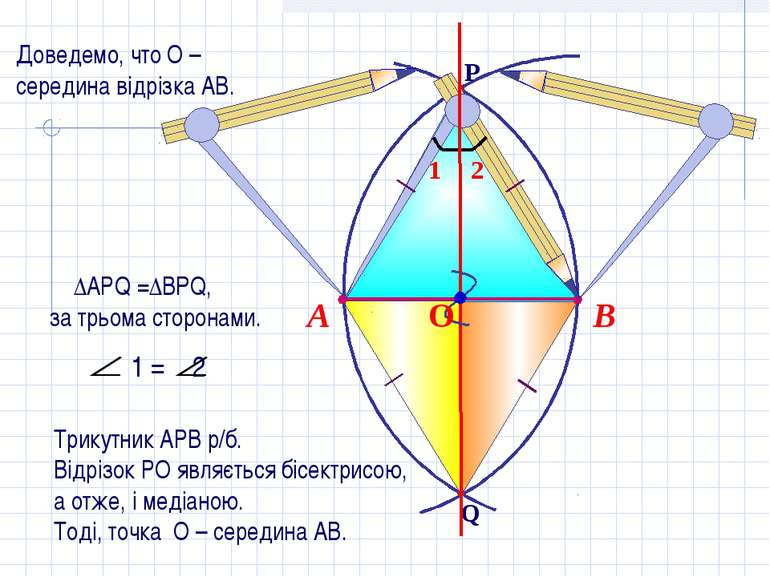
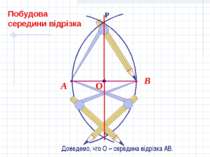
В А Трикутник АРВ р/б. Відрізок РО являється бісектрисою, а отже, і медіаною. Тоді, точка О – середина АВ. Доведемо, что О – середина відрізка АВ.

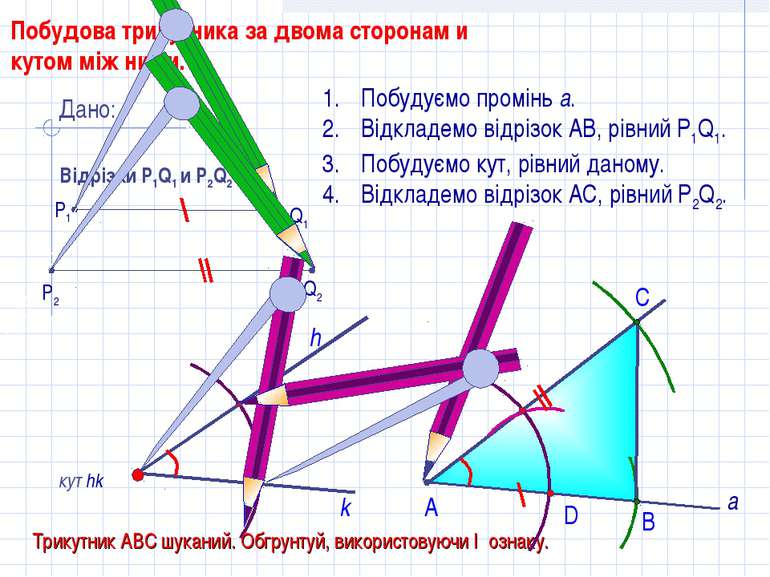
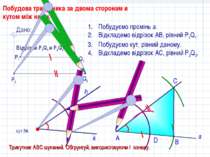
D С Побудова трикутника за двома сторонам и кутом між ними. кут hk h Побудуємо промінь а. Відкладемо відрізок АВ, рівний P1Q1. Побудуємо кут, рівний даному. Відкладемо відрізок АС, рівний P2Q2. В А Трикутник АВС шуканий. Обгрунтуй, використовуючи I ознаку. Дано: Відрізки Р1Q1 и Р2Q2 Q1 P1 P2 Q2 а k

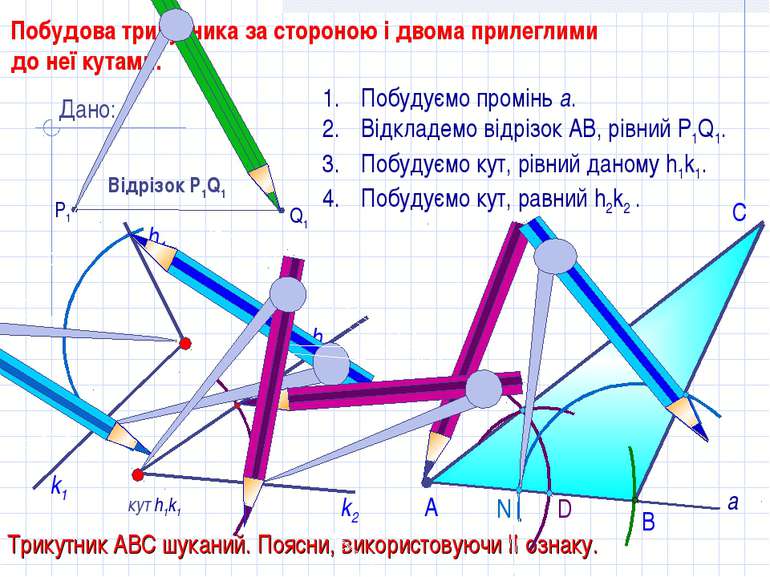
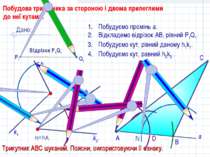
D С Побудова трикутника за стороною і двома прилеглими до неї кутами. кут h1k1 h2 Побудуємо промінь а. Відкладемо відрізок АВ, рівний P1Q1. Побудуємо кут, рівний даному h1k1. Побудуємо кут, равний h2k2 . В А Трикутник АВС шуканий. Поясни, використовуючи II ознаку. Дано: Відрізок Р1Q1 Q1 P1 а k2 h1 k1 N

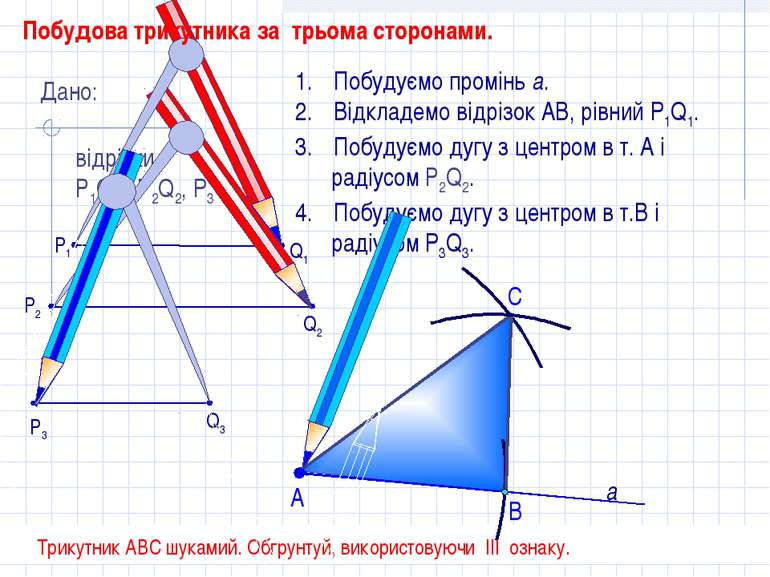
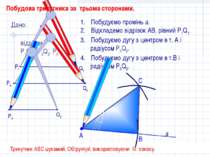
С Побудуємо промінь а. Відкладемо відрізок АВ, рівний P1Q1. Побудуємо дугу з центром в т. А і радіусом Р2Q2. Побудуємо дугу з центром в т.В і радіусом P3Q3. В А Трикутник АВС шукамий. Обгрунтуй, використовуючи III ознаку. Дано: відрізки Р1Q1, Р2Q2, P3Q3. Q1 P1 P3 Q2 а P2 Q3 Побудова трикутника за трьома сторонами.