Презентація на тему:
"Піраміда"

Виконала учениця 11-А класу Новоград-Волинської ЗОШ №7 Бучинська Дарія Піраміда

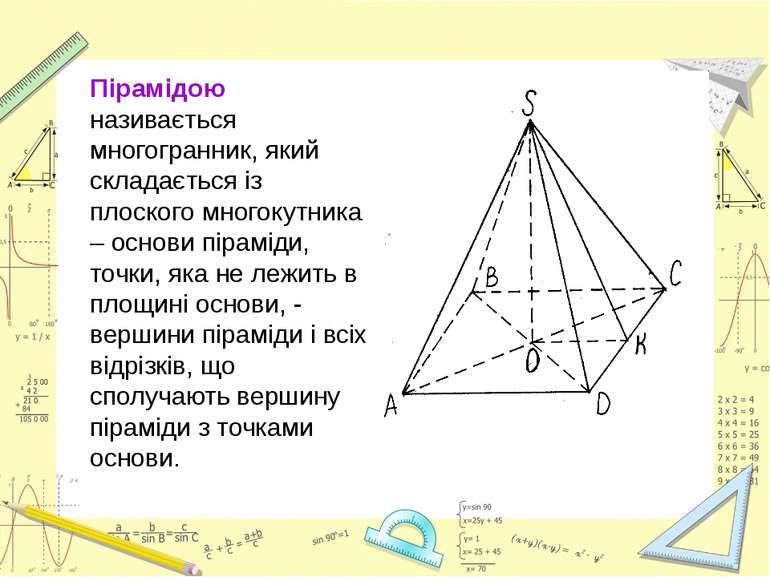
Пірамідою називається многогранник, який складається із плоского многокутника – основи піраміди, точки, яка не лежить в площині основи, - вершини піраміди і всіх відрізків, що сполучають вершину піраміди з точками основи.

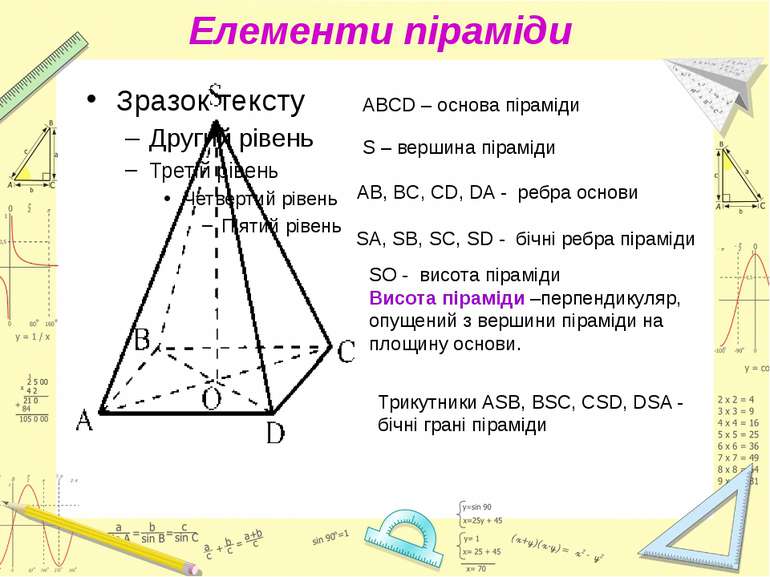
Елементи піраміди ABCD – основа піраміди S – вершина піраміди AB, BC, CD, DA - ребра основи SA, SB, SC, SD - бічні ребра піраміди SO - висота піраміди Висота піраміди –перпендикуляр, опущений з вершини піраміди на площину основи. Трикутники ASB, BSC, CSD, DSA - бічні грані піраміди

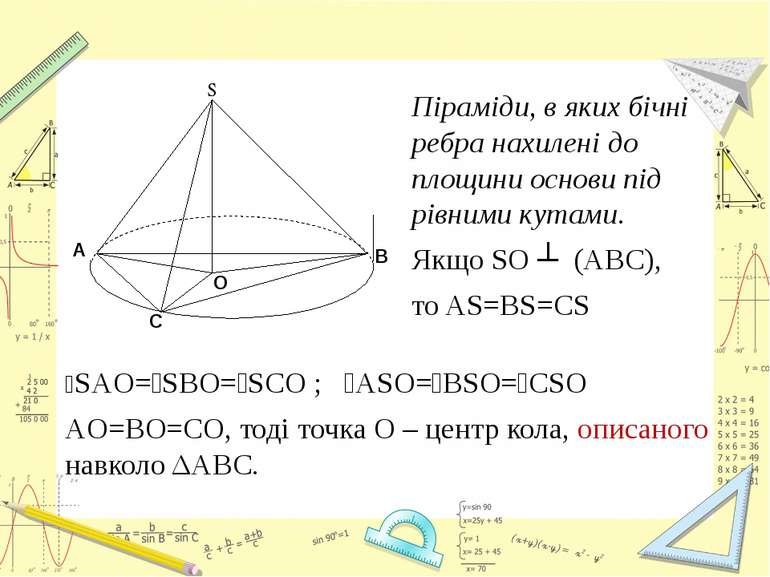
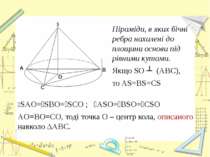
Піраміди, в яких бічні ребра нахилені до площини основи під рівними кутами. Якщо SO ┴ (ABC), то AS=BS=CS ےSAO=ےSBO=ےSCO ; ےASO=ےBSO=ےCSO AO=BO=CO, тоді точка О – центр кола, описаного навколо ΔABC.

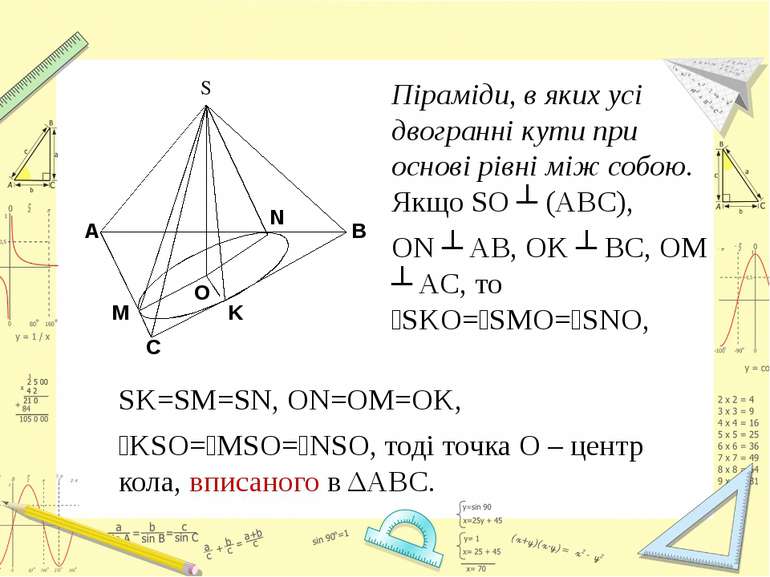
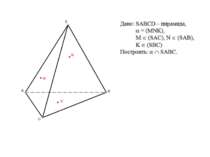
Піраміди, в яких усі двогранні кути при основі рівні між собою. Якщо SO ┴ (ABC), ON ┴ AB, OK ┴ BC, OM ┴ AC, то ےSKO=ےSMO=ےSNO, SK=SM=SN, ON=OM=OK, ےKSO=ےMSO=ےNSO, тоді точка О – центр кола, вписаного в ΔABC.

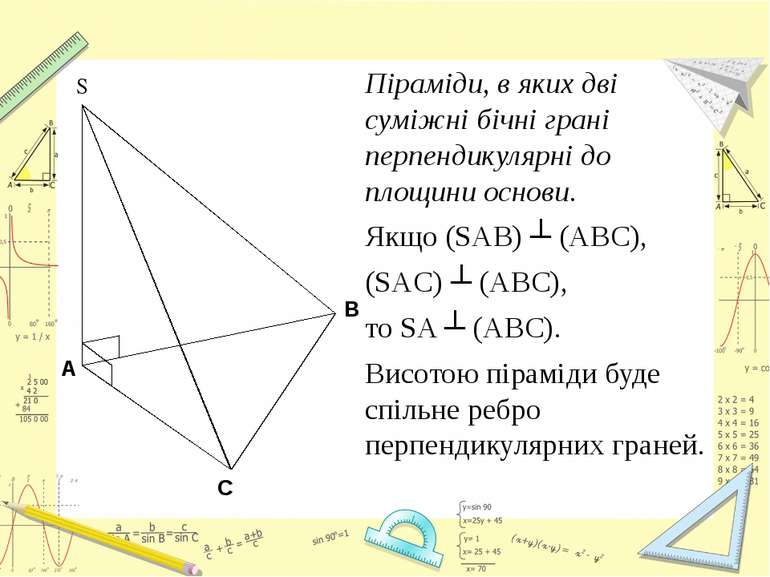
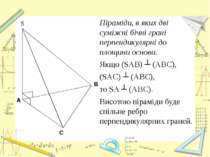
Піраміди, в яких дві суміжні бічні грані перпендикулярні до площини основи. Якщо (SAB) ┴ (ABC), (SAC) ┴ (ABC), то SA ┴ (ABC). Висотою піраміди буде спільне ребро перпендикулярних граней.

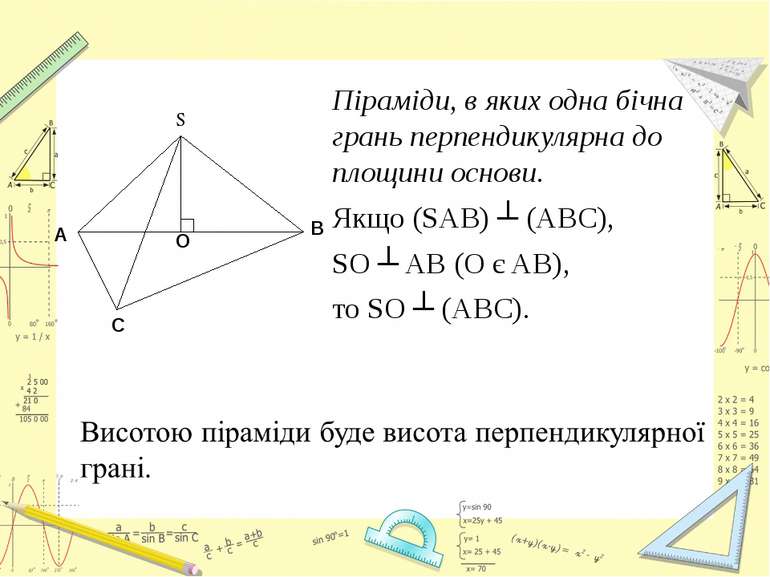
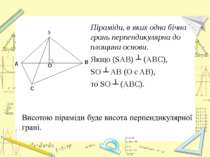
Піраміди, в яких одна бічна грань перпендикулярна до площини основи. Якщо (SAB) ┴ (ABC), SO ┴ AB (O є AB), то SO ┴ (ABC).

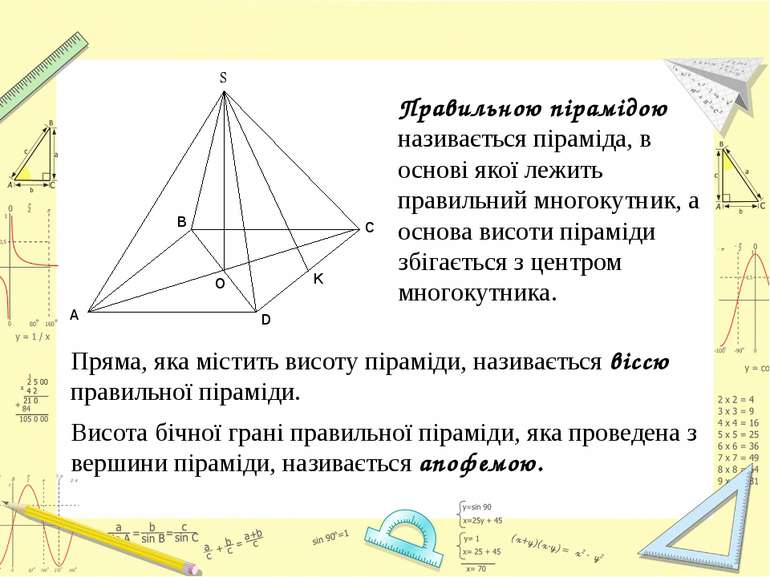
Правильною пірамідою називається піраміда, в основі якої лежить правильний многокутник, а основа висоти піраміди збігається з центром многокутника. Пряма, яка містить висоту піраміди, називається віссю правильної піраміди. Висота бічної грані правильної піраміди, яка проведена з вершини піраміди, називається апофемою.

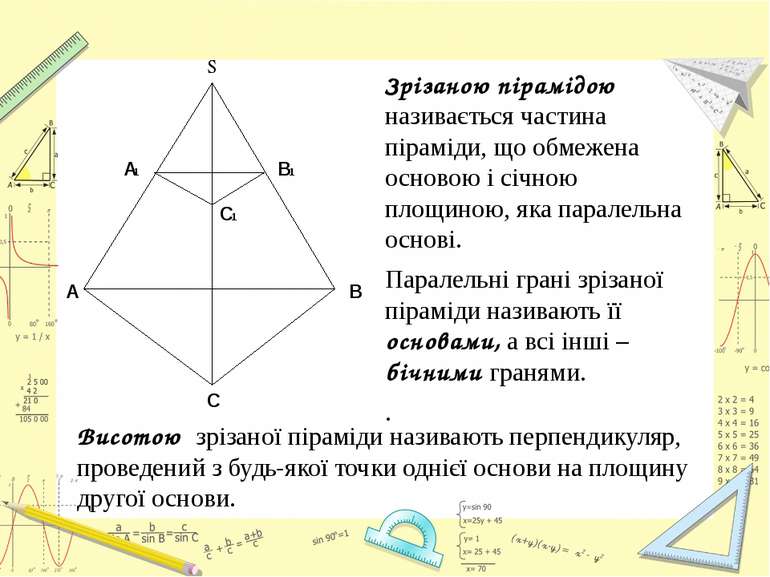
Зрізаною пірамідою називається частина піраміди, що обмежена основою і січною площиною, яка паралельна основі. Паралельні грані зрізаної піраміди називають її основами, а всі інші – бічними гранями. . Висотою зрізаної піраміди називають перпендикуляр, проведений з будь-якої точки однієї основи на площину другої основи.

Назва формули Формула Позначення Площа повної поверхні Sп=S+Sб S– площа основи; Sб– площа бічної поверхні Площа бічної поверхні Sб=½·P·l Sб=S/ cosα Р – периметр основи; l –апофема; α– двогранний кут при основі Об’ємдовільної зрізаної піраміди V = ⅓·H·(S1+S2+√S1·S2) S1,S2– площі основ; Об’ємправильної зрізаної піраміди V = ½·(P1+P2)·l P1, P2–периметриоснов Об’ємпіраміди V =⅓·S·H