Презентація на тему:
Паралелепіпед. Варіант 1

Задано паралелепіпед ABCDA1B1C1D1

Задано паралелепіпед ABCDA1B1C1D1 А А1 В1 B D1 D С1 C

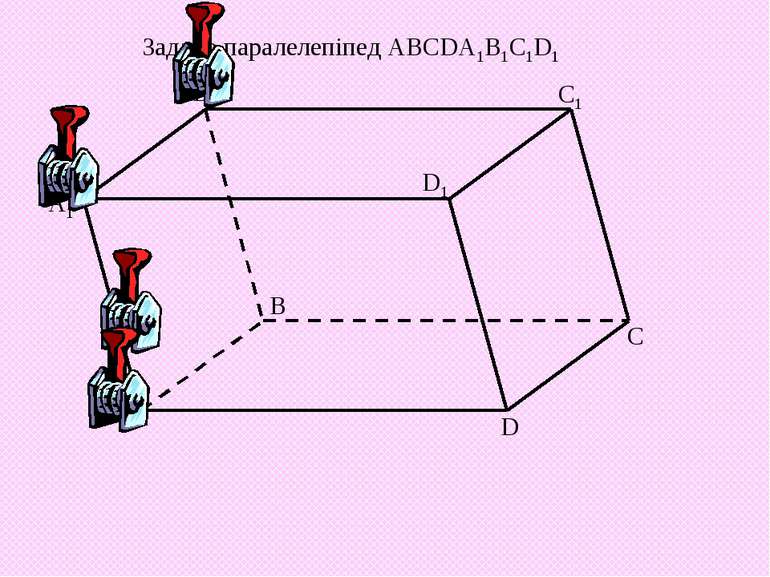
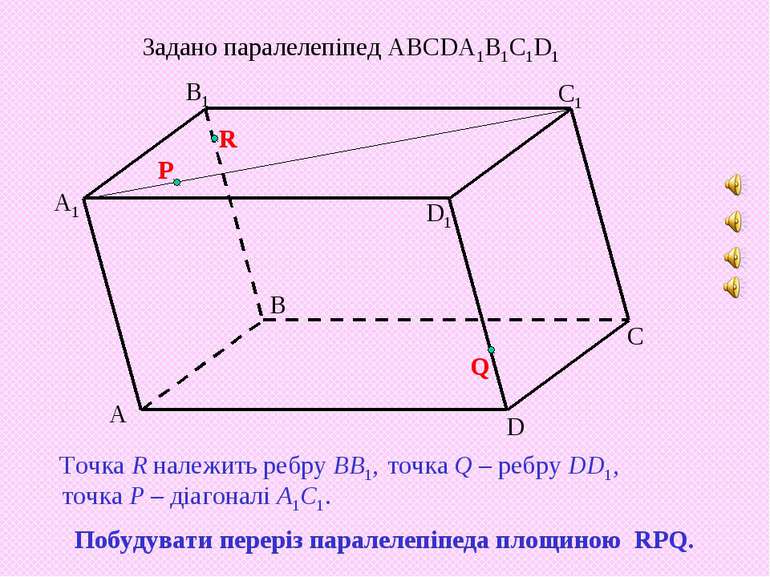
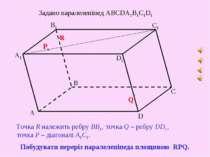
А1 В1 С1 D1 А B C D Задано паралелепіпед ABCDA1B1C1D1 Побудувати переріз паралелепіпеда площиною RPQ. Точка R належить ребру ВВ1, точка Q – ребру DD1, точка Р – діагоналі А1С1.

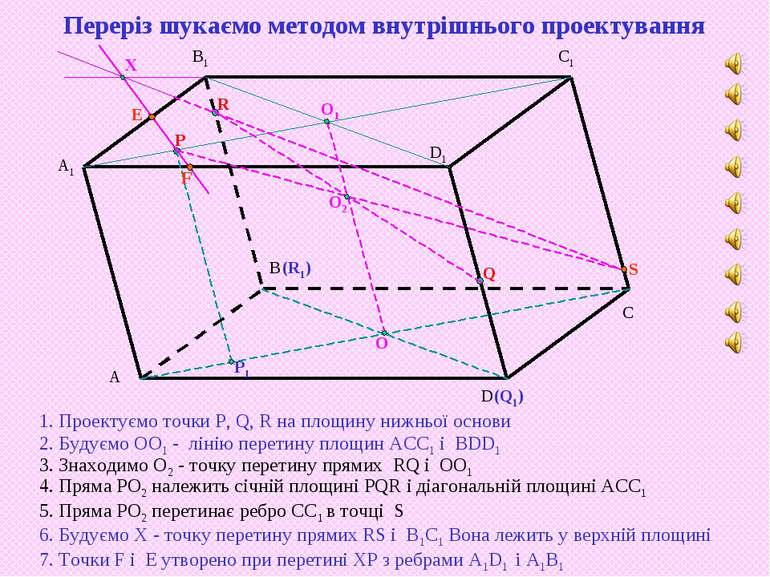
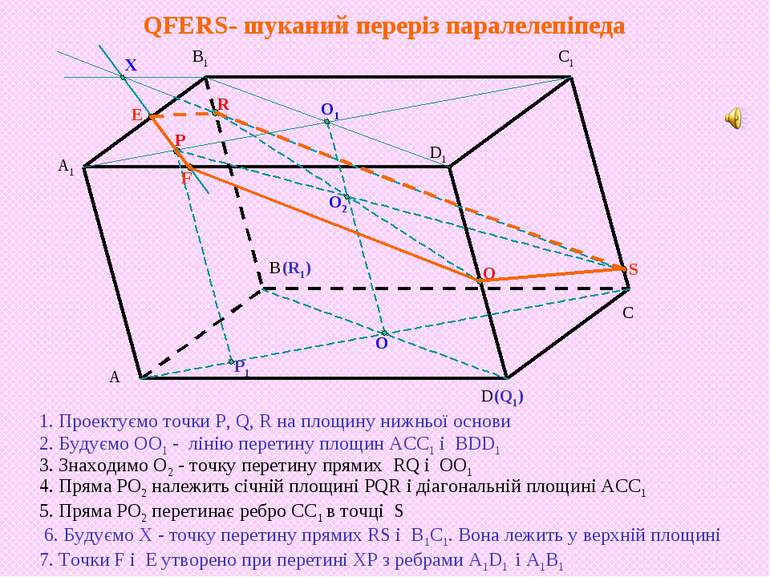
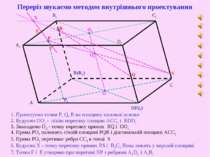
P R Q 1. Проектуємо точки P, Q, R на площину нижньої основи Р1 (Q1) (R1) O O1 O2 2. Будуємо ОО1 - лінію перетину площин АСС1 і BDD1 4. Пряма РО2 належить січній площині PQR і діагональній площині ACC1 3. Знаходимо О2 - точку перетину прямих RQ і ОО1 5. Пряма РО2 перетинає ребро CC1 в точці S S X E F 6. Будуємо Х - точку перетину прямих RS і B1C1 Вона лежить у верхній площині 7. Точки F і E утворено при перетині ХР з ребрами А1D1 i A1B1 Переріз шукаємо методом внутрішнього проектування

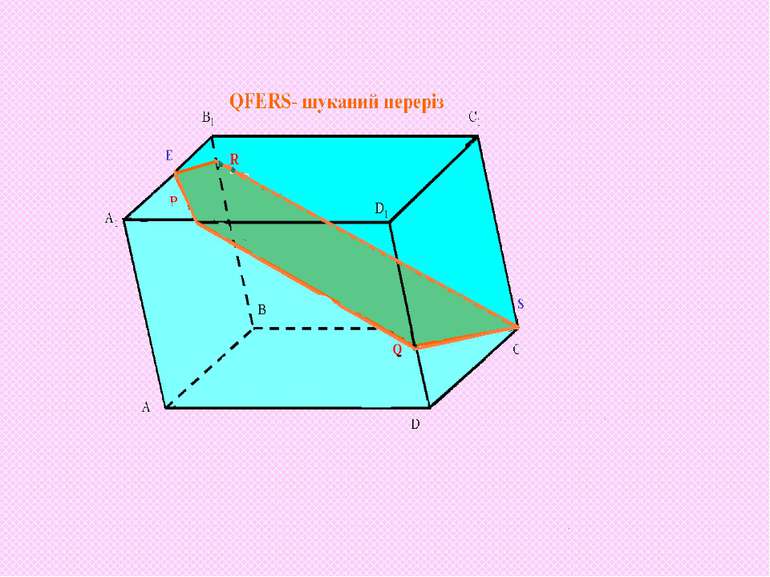
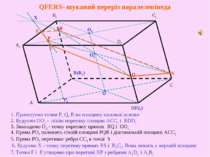
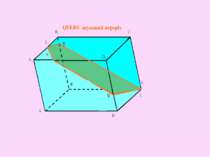
P R Q 1. Проектуємо точки P, Q, R на площину нижньої основи Р1 (Q1) (R1) O O1 O2 2. Будуємо ОО1 - лінію перетину площин АСС1 і BDD1 4. Пряма РО2 належить січній площині PQR і діагональній площині ACC1 3. Знаходимо О2 - точку перетину прямих RQ і ОО1 5. Пряма РО2 перетинає ребро CC1 в точці S S X E F 6. Будуємо Х - точку перетину прямих RS і B1C1. Вона лежить у верхній площині 7. Точки F і E утворено при перетині ХР з ребрами А1D1 i A1B1 QFERS- шуканий переріз паралелепіпеда