Презентація на тему:
Геометрія. Вступний урок

Геометрия Шевченко Н.А. Для 7 класса

Введение: Геометрия наука, занимающаяся изучением геометрических фигур. На уроках геометрии мы познакомимся с новыми фигурами и со многими важными и интересными свойствами уже известных вам фигур. Вы узнаете о том, как используются свойства геометрических фигур в практической деятельности. Материал данной презентации посвящен введению основных геометрических понятий. Наглядное представление о простейших геометрических фигурах и их свойствах, признаки равенства треугольников, признаки параллельности прямых.

Основная цель: - Научить использовать геометрический язык для описания предметов окружающего мира. Систематизировать знания учащихся об основных простейших геометрических фигурах, ввести понятия равенство отрезков. Распознавать на чертежах и моделях геометрические фигуры (отрезки, прямые, лучи, углы). - Расширить знания учащихся о треугольнике. - Дать систематические сведения о параллельности прямых, ввести аксиому параллельных прямых. - Введение терминологии. Наглядное изображение планиметрических фигур и простейших геометрических конфигураций. Показать измерительные инструменты. Познакомить с единицами измерения.

Простейшие геометрические фигуры O A Точка Прямая Плоскость

«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг – геометрия» Ле Корбюзье

Даже дом и его части – геометрические фигуры

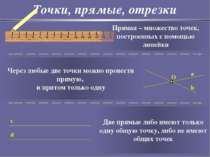
Точки, прямые, отрезки «Точка» в русском языке – конец заточенного гусиного пера. A C B D «Точка есть то, что не имеет частей» Евклид

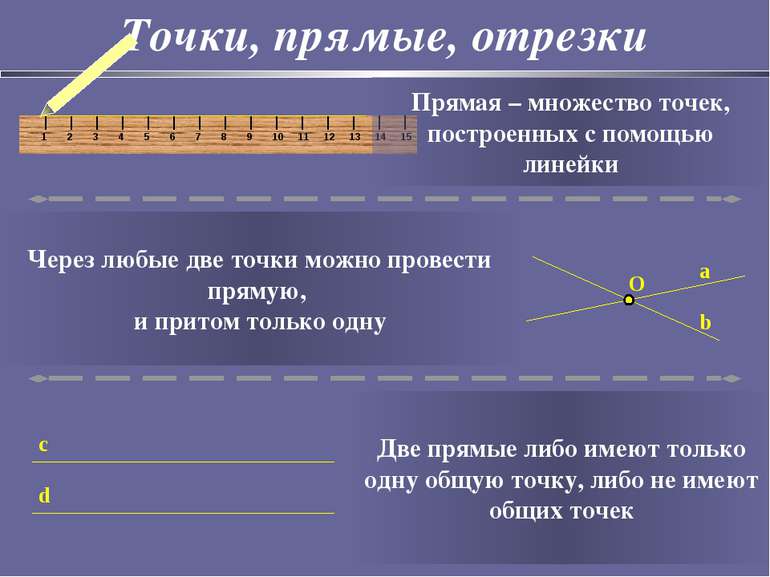
Точки, прямые, отрезки Прямая – множество точек, построенных с помощью линейки Через любые две точки можно провести прямую, и притом только одну c d Две прямые либо имеют только одну общую точку, либо не имеют общих точек

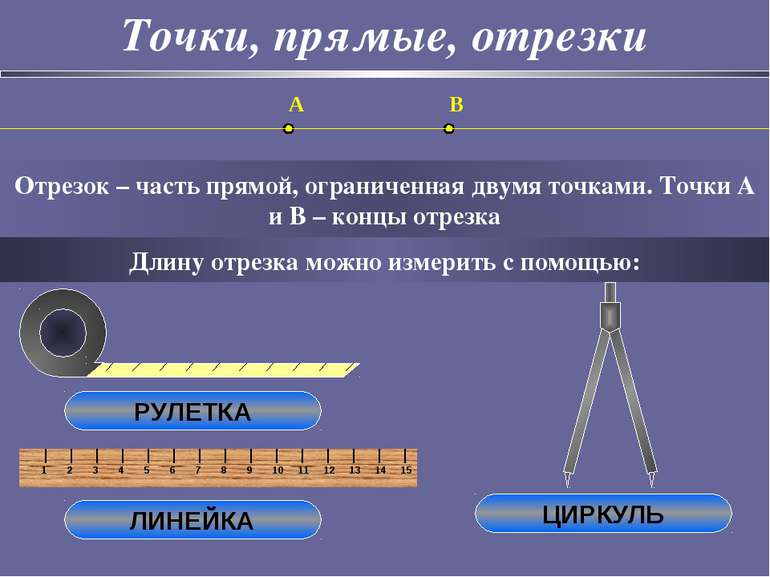
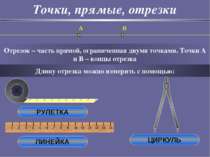
Точки, прямые, отрезки Отрезок – часть прямой, ограниченная двумя точками. Точки A и B – концы отрезка A B Длину отрезка можно измерить с помощью: РУЛЕТКА ЛИНЕЙКА ЦИРКУЛЬ

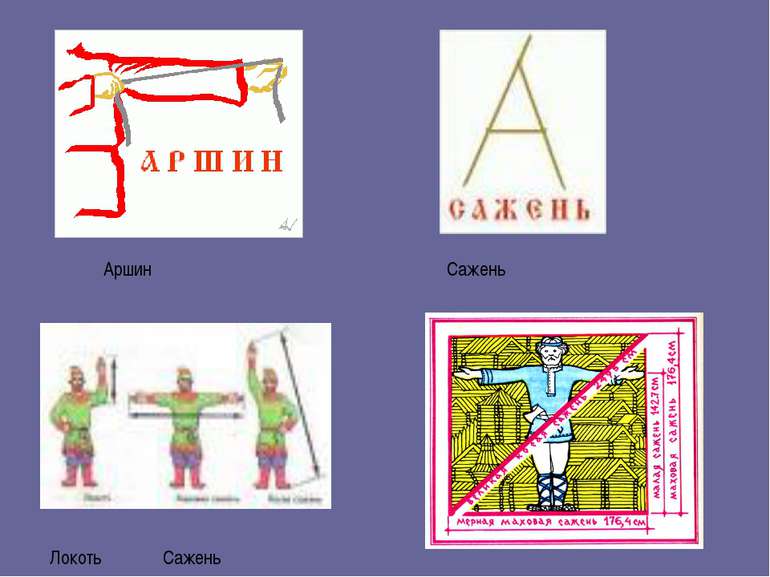
Точки, прямые, отрезки Единицы измерения длины: МЕТРИЧЕСКИЕ УСТАРЕВШИЕ Миллиметр (мм) Локоть (46-47 см) Сантиметр (см) Вершок (4,4 см) Дециметр (дм) Сажень (2,13 м) Метр (м) Аршин (71 см) Километр (км) Верста (чуть более км)

Аршин Сажень Локоть Сажень

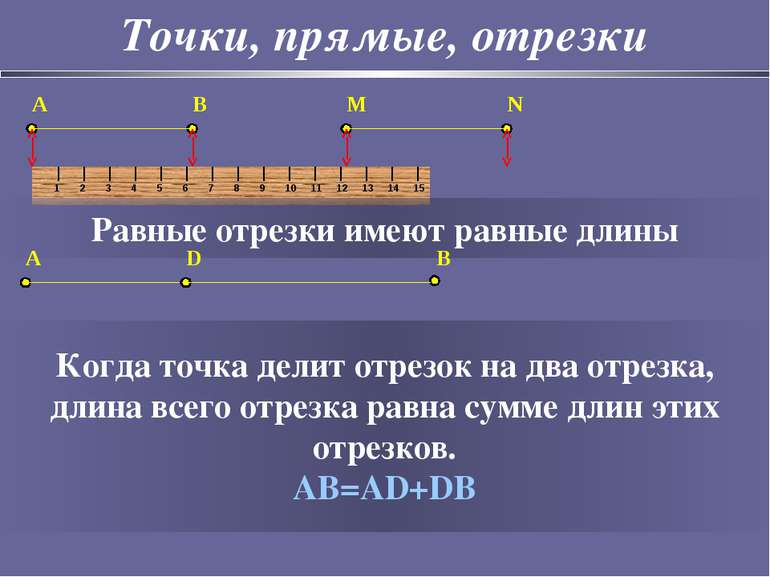
Точки, прямые, отрезки A B M N Равные отрезки имеют равные длины A D B Когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих отрезков. AB=AD+DB

Задачи: Отметьте точки F, O, и L так, что бы F и O лежали по одну сторону от L, а F и L по одну сторону от О Задача № 2 Прямая AB пересекает прямую АС в точке А, а прямую ВС в точке B. Принадлежит ли точка С прямой AB. Задача № 1 Задача №3 На сколько частей делит плоскость ее прямая?

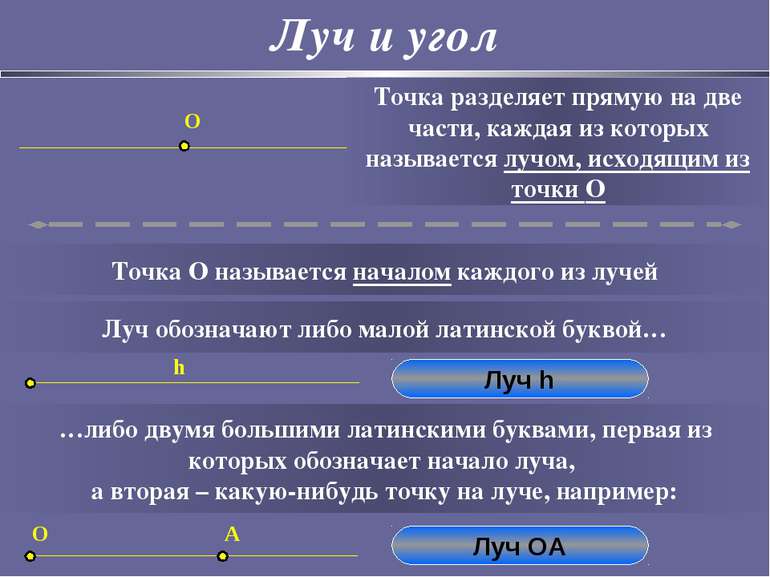
Луч и угол O Точка разделяет прямую на две части, каждая из которых называется лучом, исходящим из точки O Точка O называется началом каждого из лучей Луч обозначают либо малой латинской буквой… …либо двумя большими латинскими буквами, первая из которых обозначает начало луча, а вторая – какую-нибудь точку на луче, например: Луч h Луч OA

Луч и угол Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. O A B k h Угол Угол называется развернутым, если обе его стороны лежат на одной прямой. p q С Развернутый угол

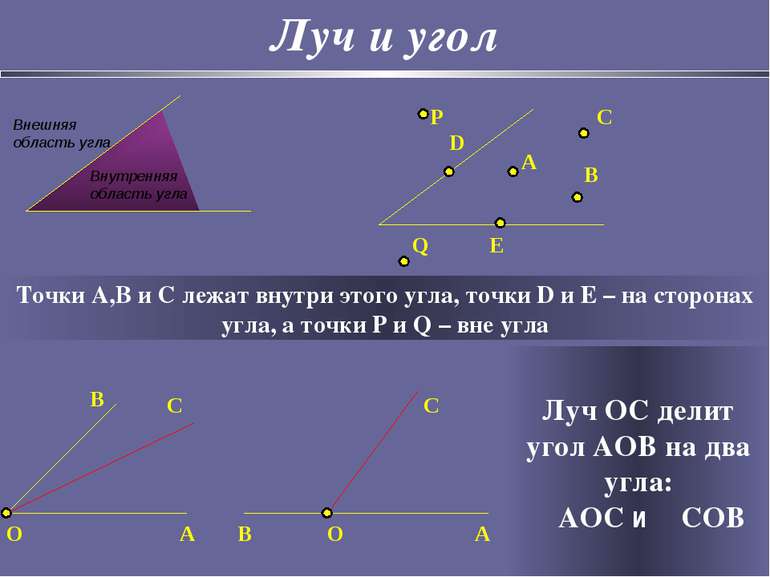
Луч и угол Точки A,B и C лежат внутри этого угла, точки D и E – на сторонах угла, а точки P и Q – вне угла Луч OC делит угол AOB на два угла: ∠AOC и ∠COB

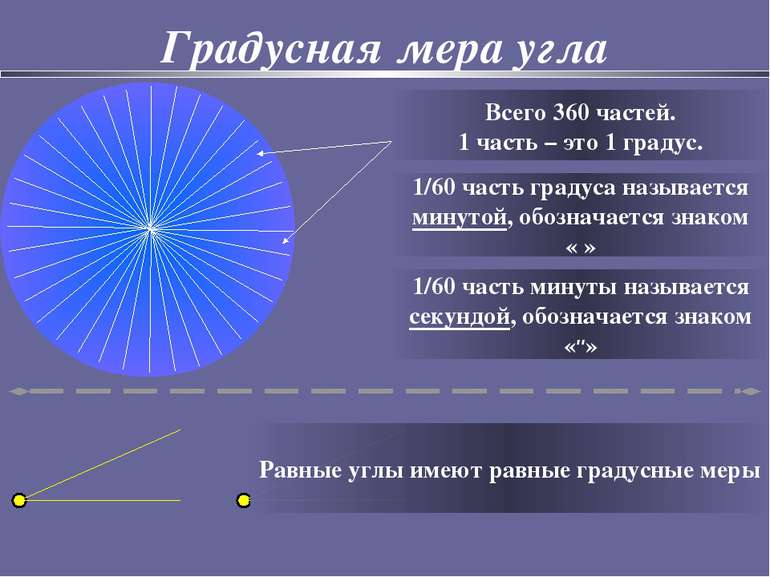
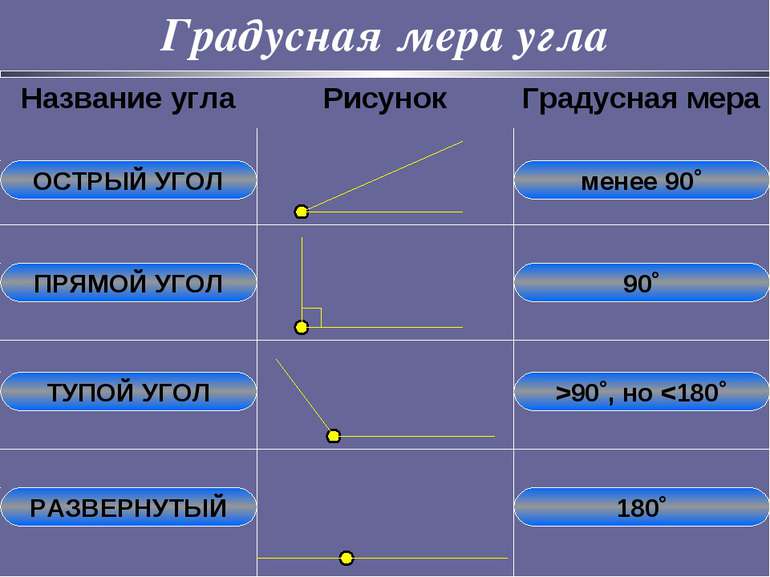
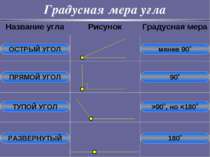
Градусная мера угла Всего 360 частей. 1 часть – это 1 градус. 1/60 часть градуса называется минутой, обозначается знаком «′» 1/60 часть минуты называется секундой, обозначается знаком «″» Равные углы имеют равные градусные меры

УГЛЫ ЧЕРТИМ И ИЗМЕРЯЕМ С ПОМОЩЬЮ ТРАНСПАРТИРА

АЛГОРИТМ ИЗМЕРЕНИЯ УГЛОВ. 1)Совместить вершину угла с центром транспортира.

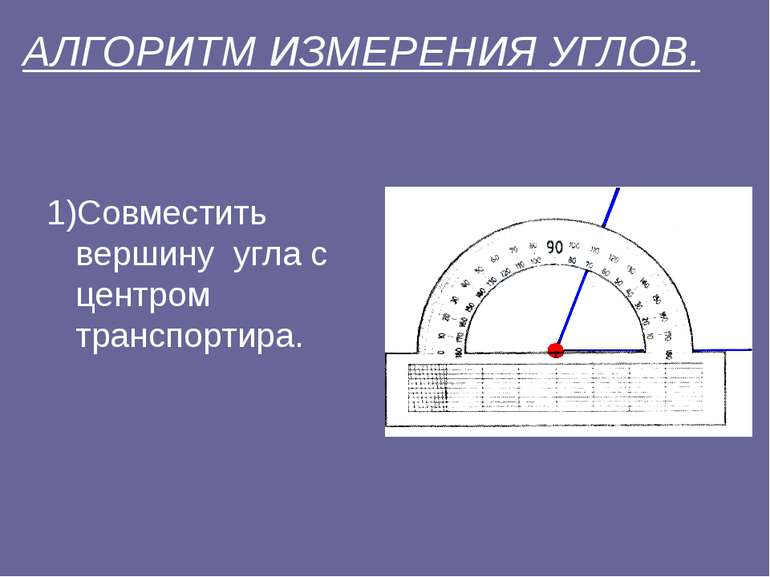
2) Расположить транспортир так, чтобы одна из сторон угла проходила через начало отсчета на шкале транспортира ( то есть совместить с 0º).

3) Найти штрих на шкале, через который проходит вторая сторона.

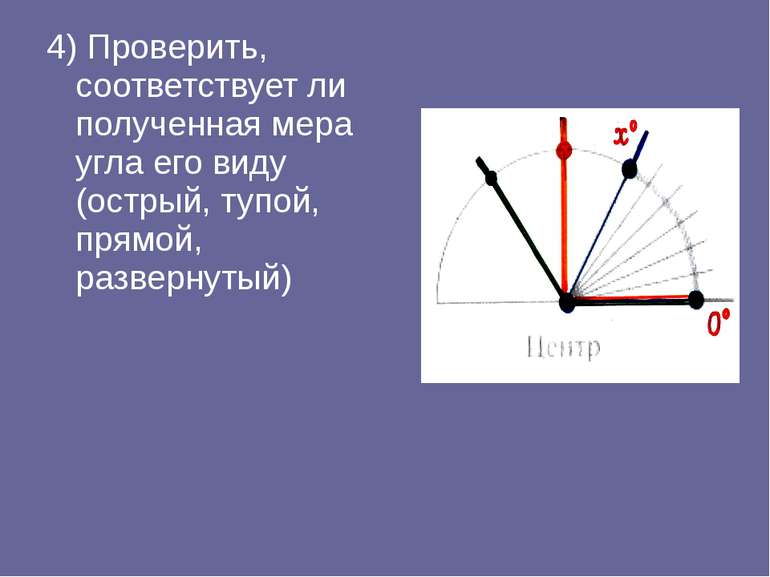
4) Проверить, соответствует ли полученная мера угла его виду (острый, тупой, прямой, развернутый)

Градусная мера угла ОСТРЫЙ УГОЛ ПРЯМОЙ УГОЛ ТУПОЙ УГОЛ РАЗВЕРНУТЫЙ менее 90˚ 90˚ >90˚, но

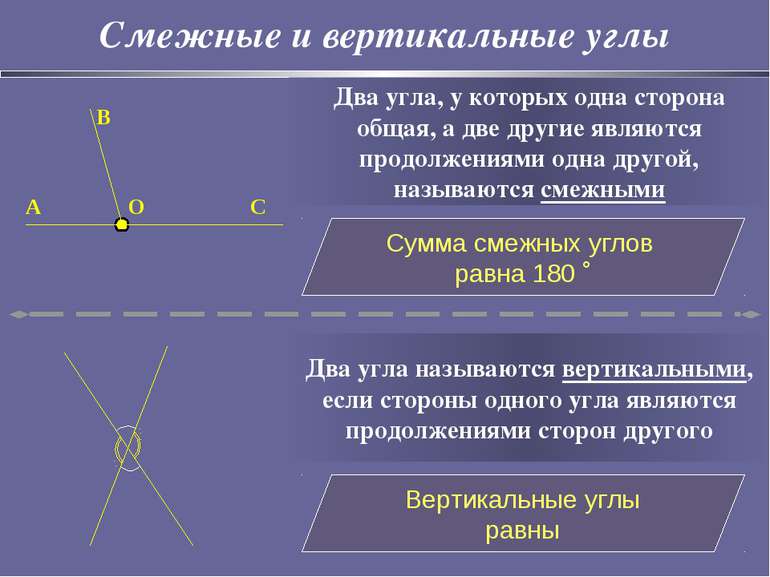
Смежные и вертикальные углы Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными Сумма смежных углов равна 180 ˚ Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого Вертикальные углы равны

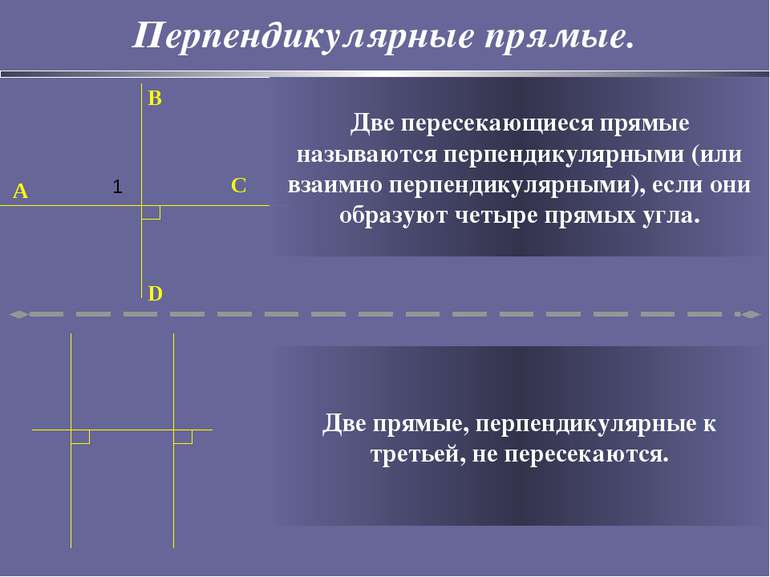
Перпендикулярные прямые. B D C A 1 Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла. Две прямые, перпендикулярные к третьей, не пересекаются.

Задачи: Задача № 1 Найдите меры смежных углов, которые относятся как: а) 4:5 б) 3:2 Задача № 2 Мера одного из двух смежных углов равно 50 градусов. Найдите меру другого угла. Постройте эти углы

Параллельные прямые

Определение Две прямые на плоскости называются параллельными, если они не пересекаются a b

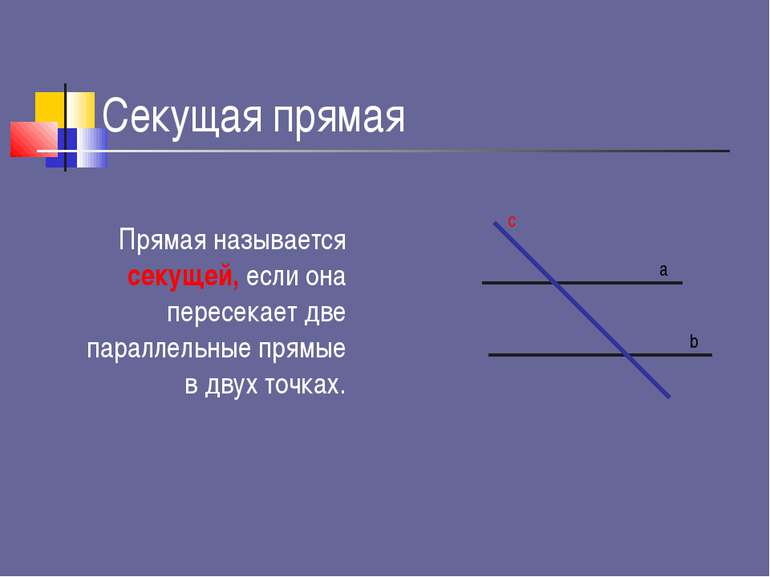
Секущая прямая Прямая называется секущей, если она пересекает две параллельные прямые в двух точках. c a b

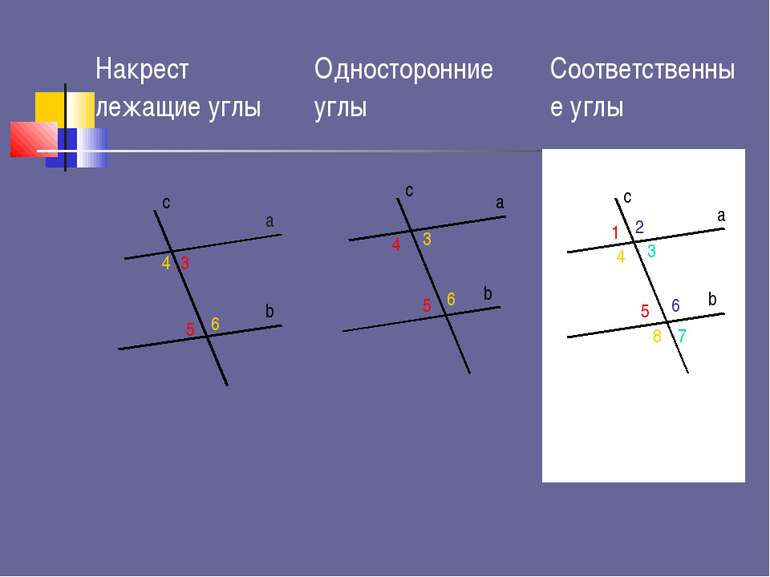
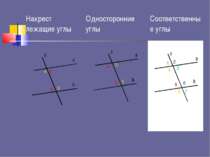
a b c c a b c a b 3 5 4 6 5 3 4 6 1 5 4 8 2 6 3 7 Накрест лежащие углы Односторонние углы Соответственные углы

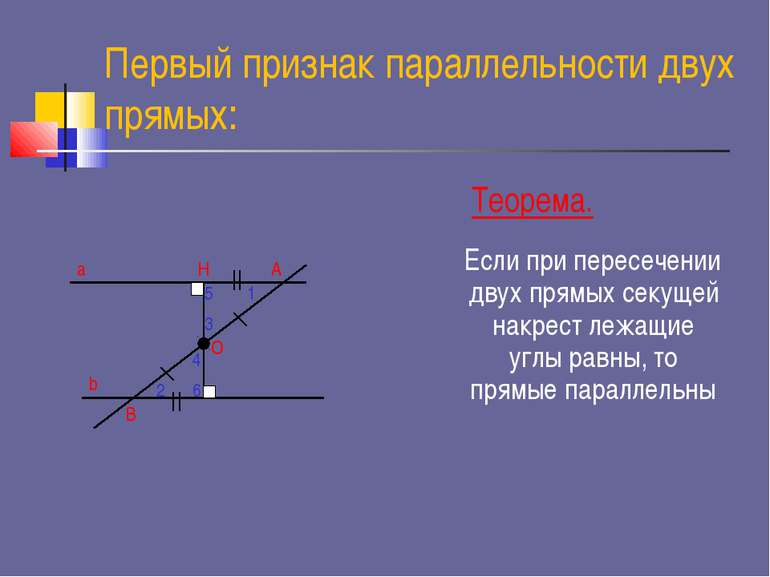
Первый признак параллельности двух прямых: Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны Теорема.

Второй признак параллельности двух прямых: Теорема. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны 1 2 3 1 = 2 = 3

Третий признак параллельности двух прямых: Теорема. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Построение параллельных прямых

Аксиомы Аксиома – утверждение, не требующее доказательств Само слово « аксиома » происходит от греческого «аксиос», что означает «ценный, достойный». Древнегреческий ученый Евклид первым придумал аксиомы, которые были изложены в его знаменитом сочинении «Начала».

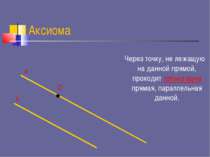
Аксиома Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. а b О

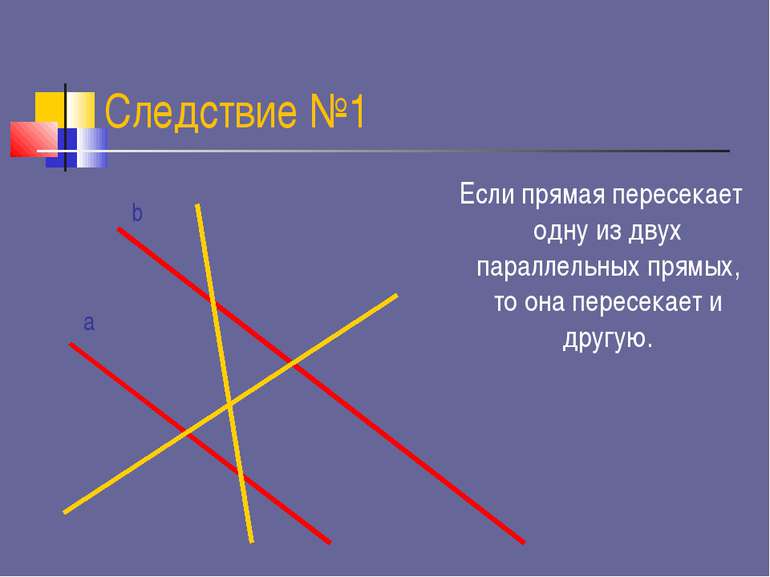
Следствие №1 Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. a b

Следствие №2 Если две прямые параллельны третьей, то они параллельны.

«Если бы мне пришлось начать вновь своё обучение, то я последовал бы совету Платона и принялся бы сперва за математику». Галилей Г.

Задачи: Задача № 1 Как можно построить параллельные прямые с помощью треугольника? Задача №2 Закончите предложение: «Чтобы узнать, параллельны ли данные прямые, нужно провести их секущую и измерить соответствующие углы. Если…»

Координатная плоскость

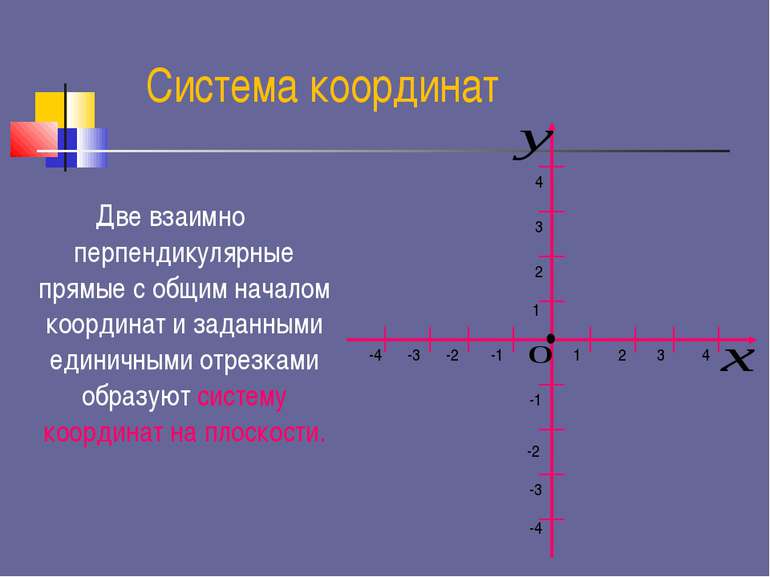
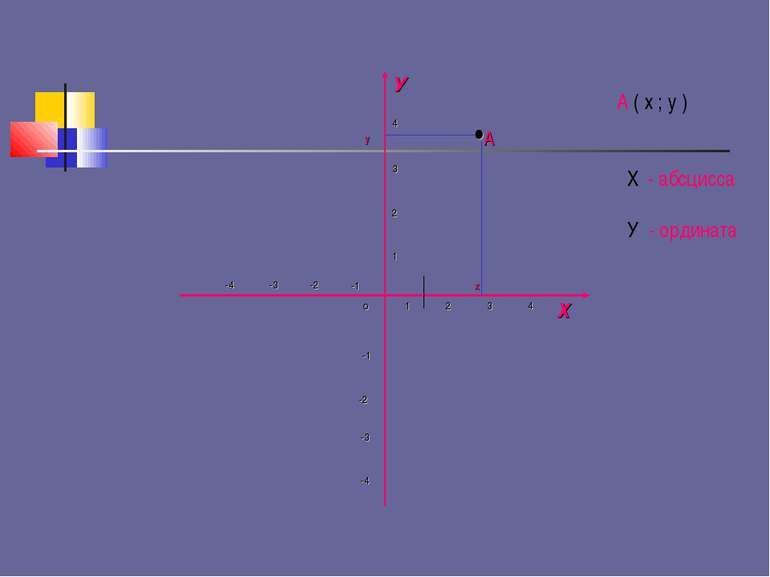
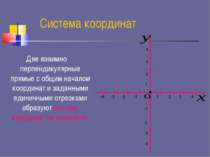
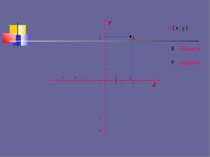
Система координат Две взаимно перпендикулярные прямые с общим началом координат и заданными единичными отрезками образуют систему координат на плоскости. 1 2 2 1 3 3 4 4 -1 -1 -2 -2 -3 -3 -4 -4 •

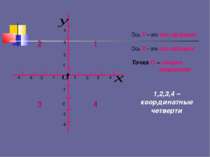
1 2 2 1 3 3 4 4 -1 -1 -2 -2 -3 -3 -4 -4 • Ось У – это ось ординат Ось Х – это ось абсцисс Точка О – начало координат 1,2,3,4 – координатные четверти 2 1 3 4

А ( х ; у ) Х - абсцисса У - ордината У у 4 •А 3 2 -4 -3 -2 -1 1 х о 1 2 3 4 Х -1 -2 -3 -4

В 1637 году Рене Декарт в книге «Геометрия « дал описание применения координат, поэтому прямоугольную систему координат часто называют декартовой. Слова «абсцисса» , «ордината», «координаты» первым начал использовать в конце 17 века Готфрид Вильгельм Лейбниц.