Презентація на тему:
Формування знань старшокласників про різні методи побудови та розв’язання задач стереометрії

Формування знань старшокласників про різні методи розв’язання задач стереометрії Підготувала Шаповалова С.В., вчитель математики Терезинського НВО “ЗОШ І-ІІІ ступенів – дитячий садок”

Функції розв’язування відібраної задачі: навчальна, розвивальна, діагностична прогнозуюча, тощо. Вдало підібрана задача створює умови для: засвоєння нового матеріалу; активізації, розвитку і закріплення попереднього матеріалу; розвитку прийомів розумової діяльності; мотивації навчання тощо.

Знайти відстані між мимобіжними діагоналями бічних граней прямої трикутної призми, усі ребра якої мають довжину a. Розв’язування задачі створює: умови для закріплення знань учнів про відстань між мимобіжними прямими; умови для повторення теми “ Координати і вектори в просторі ”; Умови для формування знань про різні методи розв’язування задач стереометрії : геометричний, координатний, векторний і координатно – векторний; Умови для міжпредметних зв’язків алгебри і геометрії.

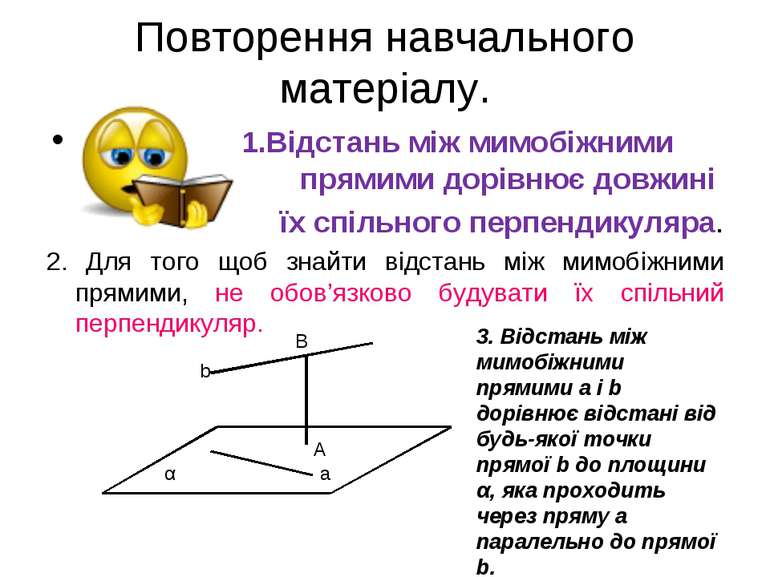
Повторення навчального матеріалу. 1.Відстань між мимобіжними прямими дорівнює довжині їх спільного перпендикуляра. 2. Для того щоб знайти відстань між мимобіжними прямими, не обов’язково будувати їх спільний перпендикуляр. b В а А α 3. Відстань між мимобіжними прямими а і b дорівнює відстані від будь-якої точки прямої b до площини α, яка проходить через пряму а паралельно до прямої b.

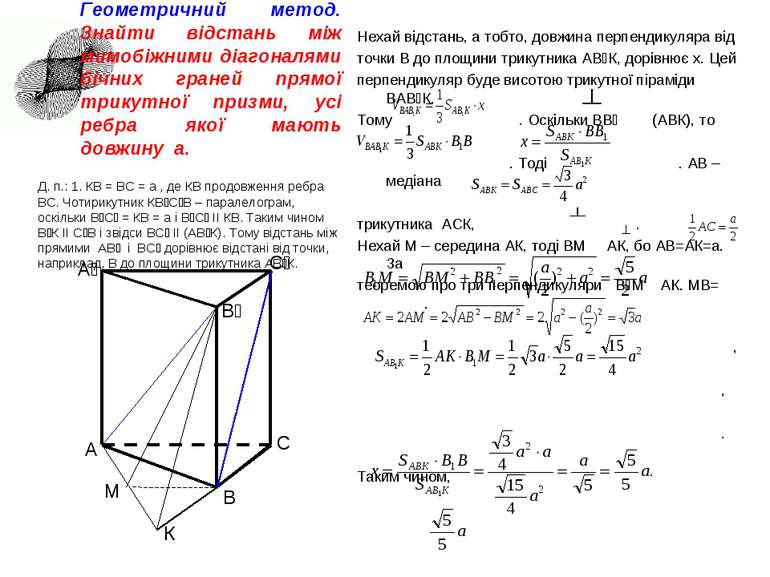
Нехай відстань, а тобто, довжина перпендикуляра від точки В до площини трикутника АВ₁К, дорівнює x. Цей перпендикуляр буде висотою трикутної піраміди ВАВ₁К. Тому . Оскільки ВВ₁ (АВК), то . Тоді . АВ – медіана трикутника АСК, . Нехай М – середина АК, тоді ВМ АК, бо АВ=АК=а. За теоремою про три перпендикуляри В₁М АК. МВ= . , , . Таким чином, Відповідь: А₁ А В С С₁ В₁ М К Д. п.: 1. КВ = ВС = а , де КВ продовження ребра ВС. Чотирикутник КВ₁С₁В – паралелограм, оскільки В₁С₁ = КВ = а і В₁С₁ ІІ КВ. Таким чином В₁К ІІ С₁В і звідси ВС₁ ІІ (АВ₁К). Тому відстань між прямими АВ₁ і ВС₁ дорівнює відстані від точки, наприклад, В до площини трикутника АВ₁К. Геометричний метод. Знайти відстань між мимобіжними діагоналями бічних граней прямої трикутної призми, усі ребра якої мають довжину a.

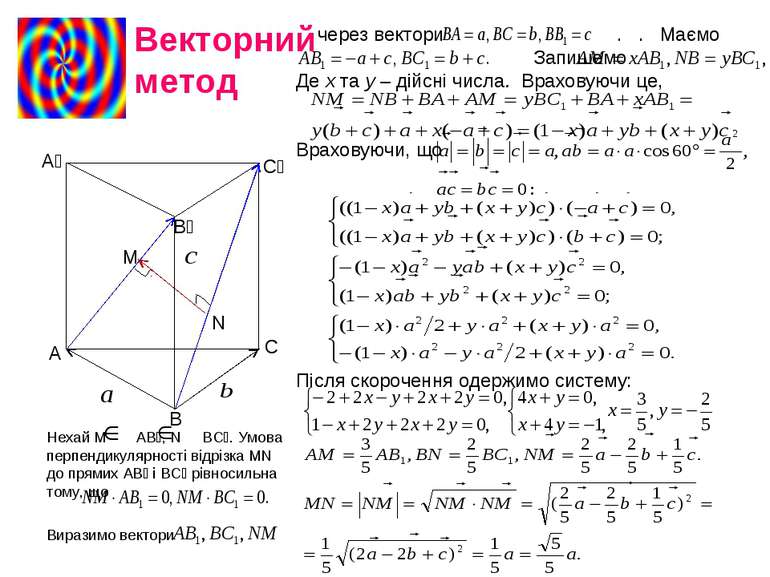
Нехай М АВ₁, N BC₁. Умова перпендикулярності відрізка МN до прямих АВ₁ і ВС₁ рівносильна тому, що Виразимо вектори Векторний метод А₁ С₁ В₁ N M A C B через вектори . . Маємо Запишемо Де х та у – дійсні числа. Враховуючи це, Враховуючи, що Після скорочення одержимо систему:

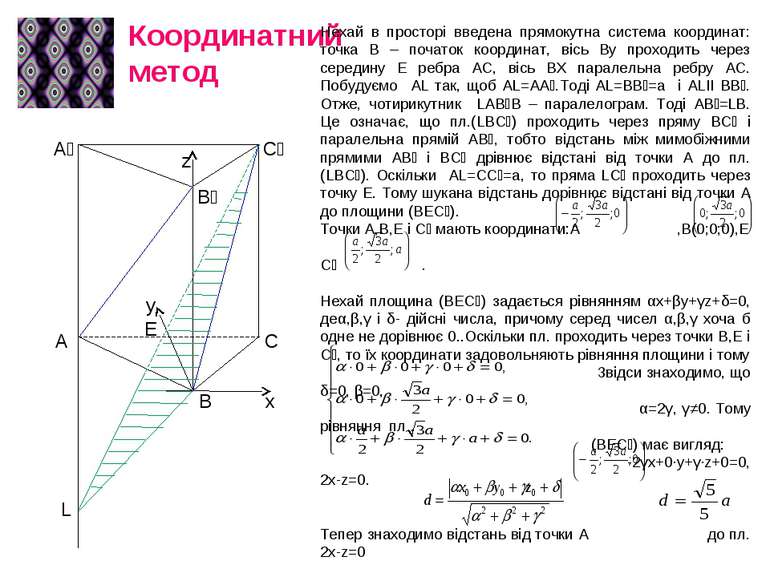
Координатний метод А₁ С₁ В₁ z x y E A B C L Нехай в просторі введена прямокутна система координат: точка В – початок координат, вісь Ву проходить через середину Е ребра АС, вісь ВХ паралельна ребру АС. Побудуємо AL так, щоб AL=AA₁.Тоді AL=BB₁=a і ALII BB₁. Отже, чотирикутник LAB₁B – паралелограм. Тоді АВ₁=LB. Це означає, що пл.(LBC₁) проходить через пряму ВС₁ і паралельна прямій АВ₁, тобто відстань між мимобіжними прямими АВ₁ і ВС₁ дрівнює відстані від точки А до пл. (LBC₁). Оскільки AL=CC₁=a, то пряма LC₁ проходить через точку Е. Тому шукана відстань дорівнює відстані від точки А до площини (BEC₁). Точки А,В,Е і С₁ мають координати:А ,В(0;0;0),Е С₁ . Нехай площина (ВЕС₁) задається рівнянням αx+βу+γz+δ=0, деα,β,γ і δ- дійсні числа, причому серед чисел α,β,γ хоча б одне не дорівнює 0..Оскільки пл. проходить через точки В,Е і С₁, то їх координати задовольняють рівняння площини і тому Звідси знаходимо, що δ=0, β=0, α=2γ, γ≠0. Тому рівняння пл . (ВЕС₁) має вигляд: -2γx+0·у+γ·z+0=0, 2х-z=0. Тепер знаходимо відстань від точки А до пл. 2х-z=0 за формулою , одержимо .

Координатно – векторний метод Введемо прямокутну систему координат: А – початок координат, вісь Ах паралельна ребру ВС, вісь Ау перетинає ребро ВС в середині F, вісь Аz проходить через ребро АА₁ А₁ z С₁ В₁ М N F y A x B C У цій системі точки А,В,В₁ і С₁ мають координати А(0;0;0), В В₁ , С₁ . Вектори і матимуть координати: Нехай точки М і N лежать на прямих АВ₁ і ВС₁ відповідно, тоді де х і у – дійсні числа, які треба визначити так, щоб довжина відрізка МN досягала найменшого можливого значення. Скориставшись формулою координат вектора,знайдемо координати точок М і N: . Тоді довжина МN = . Виділимо повні квадрати в підкореневому виразі і знайдемо його найменше значення: . Таким чином найменше значення підкореневого виразу буде дорівнювати 1/5. Це досягатиметься при умові, що Тобто . Отже найменше значення відрізка МN дорівнює .

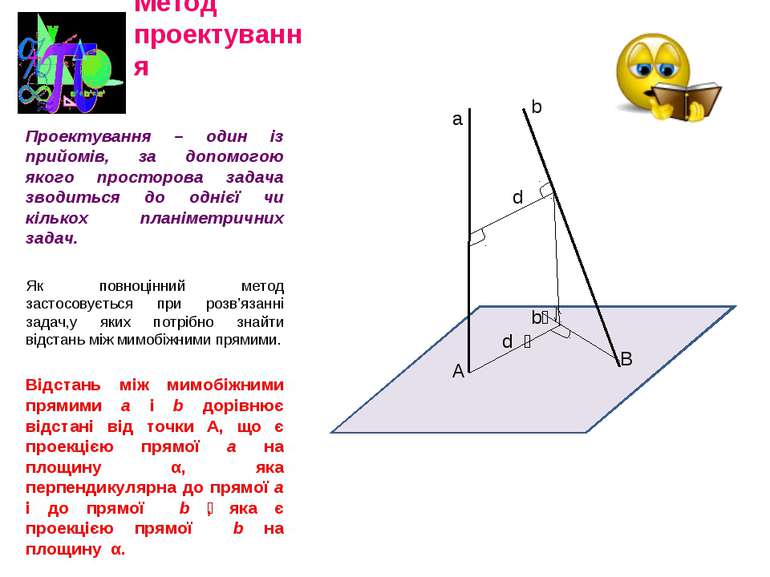
Метод проектування Проектування – один із прийомів, за допомогою якого просторова задача зводиться до однієї чи кількох планіметричних задач. Як повноцінний метод застосовується при розв’язанні задач,у яких потрібно знайти відстань між мимобіжними прямими. Відстань між мимобіжними прямими а і b дорівнює відстані від точки А, що є проекцією прямої а на площину α, яка перпендикулярна до прямої а і до прямої b , яка є проекцією прямої b на площину α. а b d А В b d

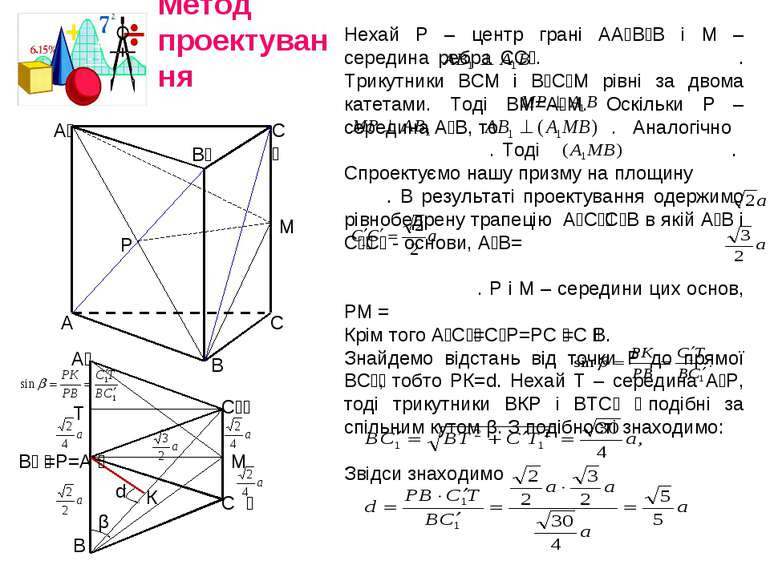
Метод проектування А В С Р М А₁ В₁ С₁ А₁ С₁ М С В В₁ =Р=А Т К d β Нехай Р – центр грані АА₁В₁В і М – середина ребра СС₁. . Трикутники ВСМ і В₁С₁М рівні за двома катетами. Тоді ВМ=А₁М. Оскільки Р – середина А₁В, то . Аналогічно . Тоді . Спроектуємо нашу призму на площину . В результаті проектування одержимо рівнобедрену трапецію А₁С₁ С₁В в якій А₁В і С₁ С₁ - основи, А₁В= . Р і М – середини цих основ, РМ = Крім того А₁С₁ =С₁Р=РС =С В. Знайдемо відстань від точки Р до прямої ВС₁ , тобто РК=d. Нехай Т – середина А₁Р, тоді трикутники ВКР і ВТС₁ подібні за спільним кутом β. З подібності знаходимо: Звідси знаходимо .