Презентація на тему:
Розв׳язання раціональних рівнянь вищих степенів

Розв׳язування раціональних рівнянь вищих степенів Презентацію розробила Кулинич Лідія Йосипівна, вчитель математики Тинівської загальноосвітньої школи І-ІІІ ступенів Жашківського району

Мета: - Систематизація і узагальнення знань про рівняння вищих степенів, типи рівнянь, методи їх розв׳язування, - розвиток вміння робити висновки, мислити від конкретного до загального, - підготовка до зовнішнього незалежного оцінювання.

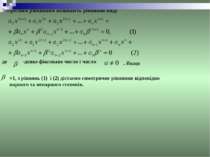
Цілим раціональним рівнянням n-го степеня називається рівняння виду Якщо a0=1, то рівняння називається зведеним. Розв’язування багатьох типів рівнянь вдається звести до розв’язування цілих раціональних рівнянь. Повторимо основні теоретичні відомості Для алгебраїчних рівнянь вищих степенів не існує єдиного загального методу розв’язування.

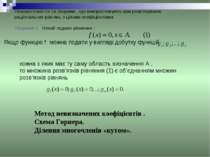
Основні поняття та теореми , що використовують при розв’язуванні раціональних рівнянь з цілими коефіцієнтами. Теорема 1. Нехай задано рівняння : Якщо функцію f можна подати у вигляді добутку функцій кожна з яких має ту саму область визначення А , то множина розв’язків рівняння (1) є об’єднанням множин розв’язків рівнянь Метод невизначених коефіцієнтів . Схема Горнера. Ділення многочленів «кутом».

Теорема Безу. Остача від ділення многочлена на двочлен дорівнює значенню цього многочленна, якщо , тобто Число називається коренем многочлена , якщо Наслідок. Якщо число є коренем многочена Р(х), то цей многочлен ділиться на двочлен без остачі. Основна теорема алгебри . Теорема Вієта. Теорема. Якщо многочлен з цілими коефіцієнтами має раціональний корінь ( ),то р є дільником вільного члена , а - дільником коефіцієнта при старшому члені Наслідок. Якщо коефіцієнт при старшому члені рівняння з цілими коефіцієнтами дорівнює 1, то всі раціональні корені цього рівняння (якщо вони існують) – цілі числа.

Методи розв'язування рівнянь вищих степенів

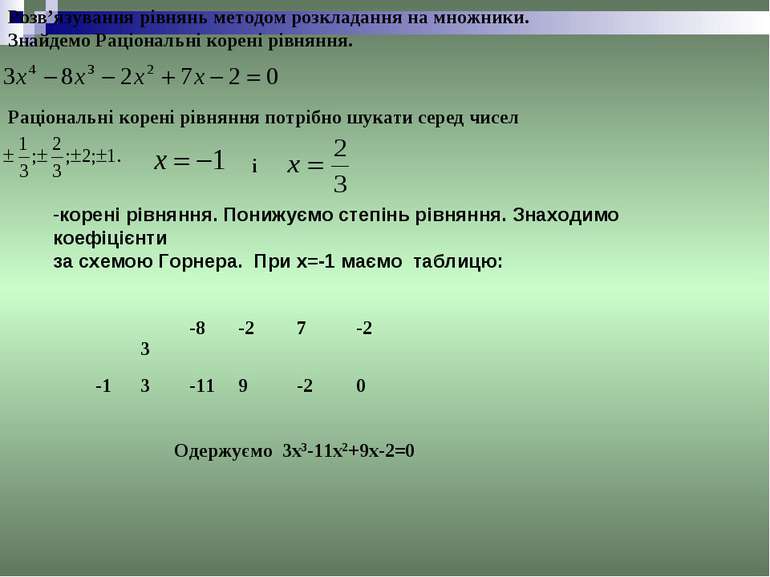
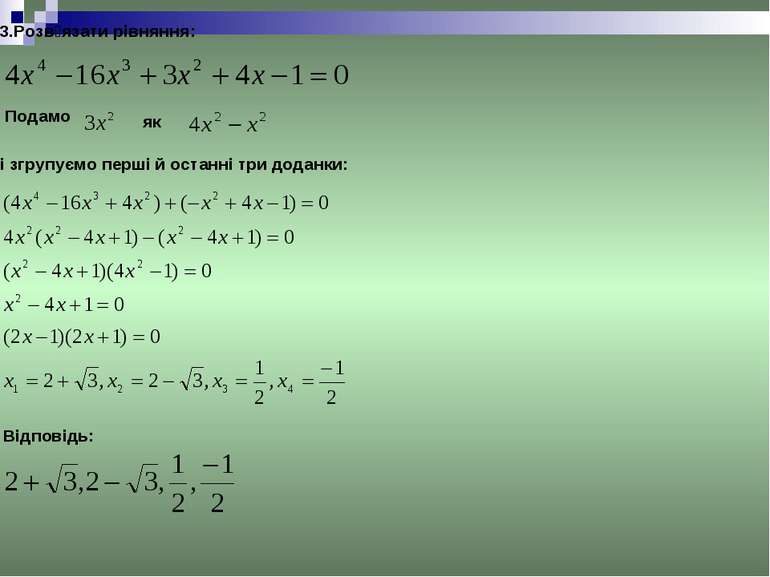
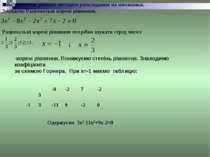
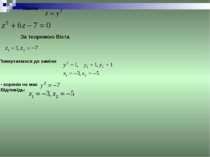
Розв’язування рівнянь методом розкладання на множники. Знайдемо Раціональні корені рівняння. Раціональні корені рівняння потрібно шукати серед чисел і корені рівняння. Понижуємо степінь рівняння. Знаходимо коефіцієнти за схемою Горнера. При x=-1 маємо таблицю: Одержуємо 3x3-11x2+9x-2=0 3 -8 -2 7 -2 -1 3 -11 9 -2 0

При Одержуємо Можемо записати, що Отже, Відповідь : 3 -11 9 -2 2/3 3 -9 3 0

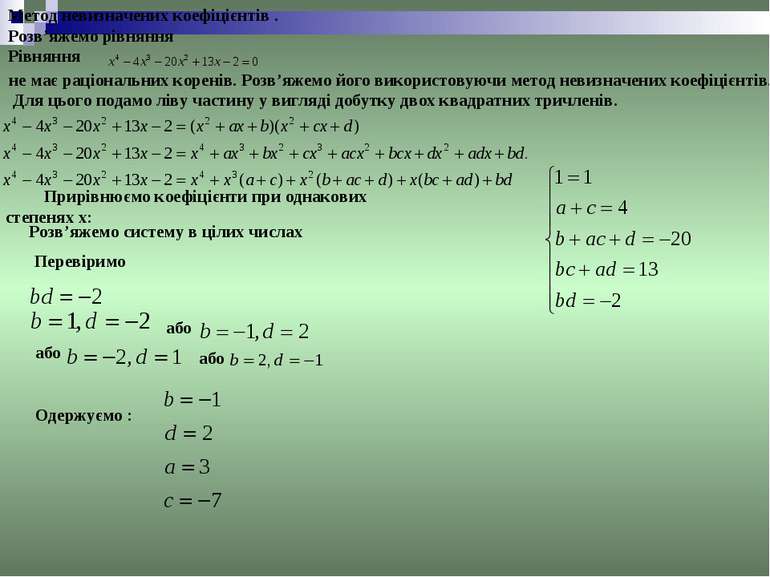
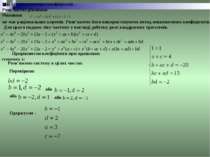
Метод невизначених коефіцієнтів . Розв’яжемо рівняння Рівняння не має раціональних коренів. Розв’яжемо його використовуючи метод невизначених коефіцієнтів. Для цього подамо ліву частину у вигляді добутку двох квадратних тричленів. Прирівнюємо коефіцієнти при однакових степенях х: Розв’яжемо систему в цілих числах Перевіримо або або або Одержуємо :

Тоді Звідки Відповідь:

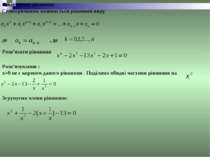
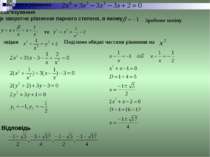
Симетричні рівняння . Симетричними називається рівняння виду де , де Розв’язати рівняння Розв’язування : х=0 не є коренем даного рівняння . Поділимо обидві частини рівняння на Згрупуємо члени рівняння:

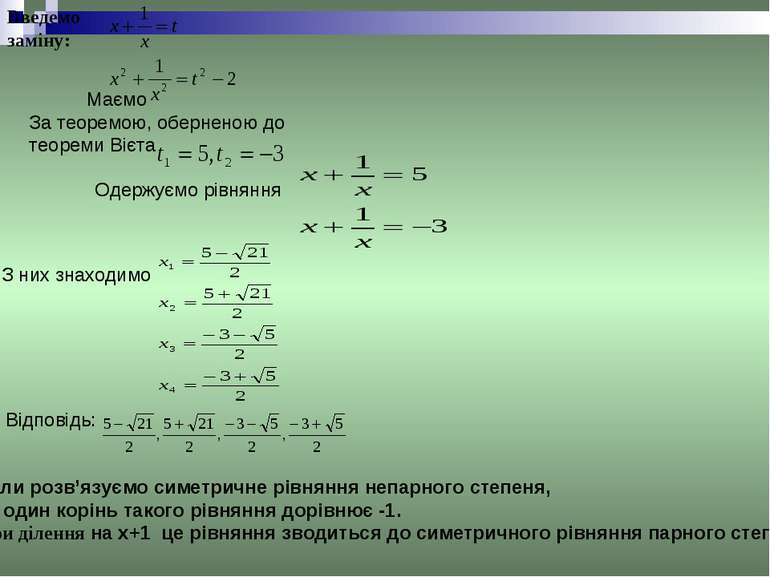
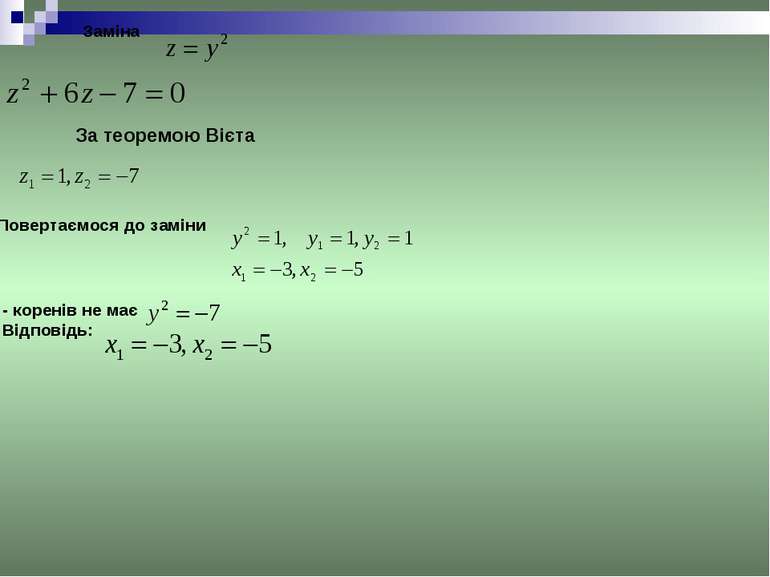
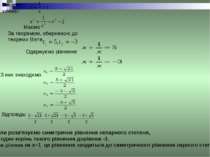
Введемо заміну: Маємо За теоремою, оберненою до теореми Вієта Одержуємо рівняння З них знаходимо Відповідь: Коли розв’язуємо симетричне рівняння непарного степеня, то один корінь такого рівняння дорівнює -1. При ділення на х+1 це рівняння зводиться до симетричного рівняння парного степеня.

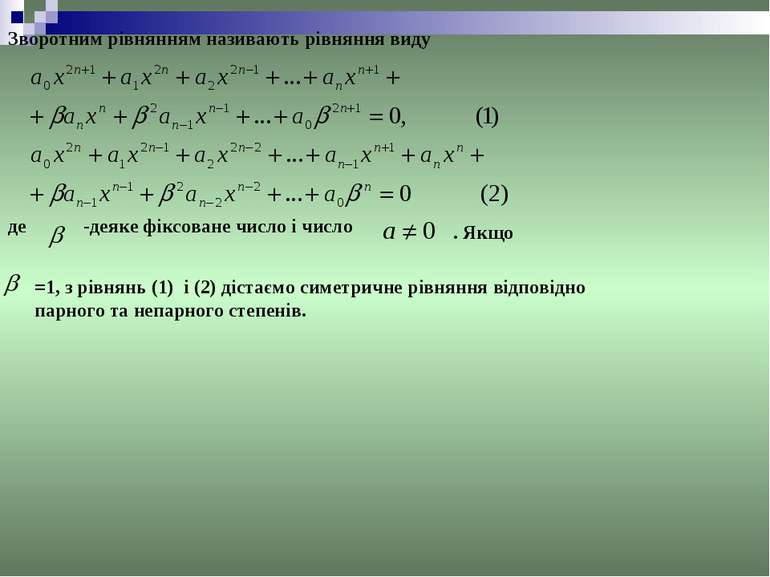
Зворотним рівнянням називають рівняння виду де -деяке фіксоване число і число . Якщо =1, з рівнянь (1) і (2) дістаємо симетричне рівняння відповідно парного та непарного степенів.

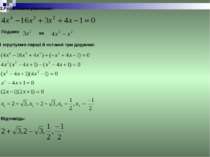
Розв’язати рівняння Розв’язування Це зворотне рівняння парного степеня, в якому Зробимо заміну то звідки Поділимо обидві частини рівняння на Відповідь:

Метод спостережень Ейлер виділяв спостереження як один з методів дослідження чисел. Про цей метод не слід забувати, приступаючи до розв’язування нестандартного рівняння. Розв’язати рівняння Розв’язування Відповідь :

2.Розв’язати рівняння Розв’язування Відповідь:

3.Розв׳язати рівняння: Подамо як і згрупуємо перші й останні три доданки: Відповідь:

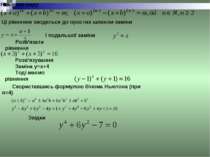
Рівняння виду Ці рівняння зводяться до простих шляхом заміни і подальшої заміни Розв’язати рівняння Розв’язування Заміна у=х+4 Тоді маємо рівняння Скориставшись формулою бінома Ньютона (при n=4) Звідки

Заміна За теоремою Вієта Повертаємося до заміни - коренів не має Відповідь:

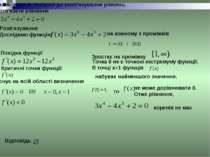
Застосування похідної до розв’язування рівнянь. Розв’язати рівняння Розв’язування Дослідимо функцію Похідна функції Критичні точки функції: існує на всій області визначення , на кожному з проміжків Зростає на проміжку Точка 0 не є точкою екстремуму функції. В точці х=1 функція набуває найменшого значення. то не може дорівнювати 0. Отже рівняння, коренів не має Відповідь:

Література: 1.Є.П.Нелін, О.Є.Долгова . Алгебра і початки аналізу.В, Світ дитинства,2005. 2.Ф.П.Яремчук, П.А.Рудченко. Алгебра і елементарні функції. В.Наукова думка,1976 3.С.Т.Завало. Рівняння і нерівності. В.Радянська щкола,1973 4.М.І.Шкіль,Т.В.Колесник, Т.М.Хмара. Алгебра і початки аналізу для поглибленого вивчення. В.Освіта,2000. 5.Ш.Г.Горделадзе, М.М.Кухарчук, Ф.П.Яремчук. Збірник конкурсних задач з математки.В.Вища школа,1976 6.Збірник задач з математики для вступників до втузів. За редакцією М.І.Сканаві. В. Вища школа,1992.