Презентація на тему:
Реляційна алгебра

Реляційна алгебра Реляційна алгебра. Операції реляційної алгебри. Особливості теоретико-множинних операцій реляційної алгебри.

Елементами основної множини є реляційні відношення. Реляційні відношення називаються сумісними, якщо: У них однакова кількість атрибутів, тобто k=n; Можна встановити взаємно однозначну відповідність між доменами атрибутів першої та другої реляцій. Тобто існує таке бієктивне відображення , що , тобто домени атрибутів однакові

Властивості бінарних операцій: Операція φ є комутативною, якщо А φ В = В φ А; Операція φ є асоціативною, якщо (А φ В) φ С = А φ (В φ С); Операція φ є дистрибутивною з операцією θ, якщо А φ (В φ С) = (А φ В) θ (А φ С)

Операція oб’єднання Нехай L — певна множина атрибутів. Об'єднанням сумісних реляційних відношень R1 і R2 зі схемами R1(L) і R2(L) (позначається як R1 U R2) називається таке реляційне відношення R зі схемою R(L), що містить кортежі обох поєднуваних відношень, але без повторень R(L) = R1 (L) R2 (L) = {r | r R1 r R2}. Операція комутативна, асоціативна й дистрибутивна щодо перетину.

Операція oб’єднання R (L) = R1 (L) U R2 (L) = { r | r є R1 v r є R2 } R1 R2 R1 U R2 А В a1 b1 a1 b2 a2 b3 А В a1 b1 a2 b1 А В a1 b1 a1 b2 a2 b1 a2 b3

Операція перетину Перетином сумісних реляційних відношень R1 і R2 зі схемами R1(L) і R2(L) (позначається як R1 ∩ R2) називається таке реляційне відношення R зі схемою R(L), яке містить кортежі, шо входять до складу обох операндів: R(L) = R1 (L) R2 (L) = {r | r R1 & r R2}. Операція комутативна, асоціативна й дистрибутивна щодо об'єднання

Операції реляційної алгебри Операція перетину R (L) = R1 (L) ∩ R2 (L) = { r | r є R1 & r є R2 } R1 R2 R1 ∩ R2 А В a1 b1 a1 b2 a2 b3 А В a1 b1 a2 b1 А В a1 b1

Операція різниці Різницею сумісних реляційних відношень R1 і R2 зі схемами R1(L) і R2(L) (позначається як R1 - R2) називається реляційне відношення R зі схемою R(L), що містить ті кортежі з першого операнда R1, яких немає у другому операнді R2: R(L) = R1 (L) - R2 (L) = {r | r R1 & r R2}. Операція не комутативна, не асоціативна й не дистрибутивна з іншими операціями.

Операція різниці R (L) = R1 (L) – R2 (L) = { r | r є R1 & r є R2 } R1 R2 R1 – R2 А В a1 b1 a1 b2 a2 b3 А В a1 b1 a2 b1 А В a1 b2 a2 b3

Операція проекції Проекцією реляційного відношення R зі схемою R(Аi,...,Аk) за атрибутами Аi1,…,Аіn, де {Аi1,..., Аіп) {А1,..., Ак}, що позначається R[Аi1,..., Аіп], називається таке відношення, кортежі якого отримані з кортежів відношення R(Аi,...,Аk) шляхом видалення значень, що не належать атрибутам, за якими виконується проекція. В кінцевому відношенні повторні екземпляри кортежів видаляються. Якщо r - кортеж відношення R, то запис r[L] - множина тих елементів кортежу r, що відповідають значенням атрибутів з L, де L — підмножина атрибутів відношення R.

Операція проекції S = R [Ain ,….., Ain] = {r [Ain ,….., Ain] | r є R} R R [A,C] АБО ¶Ai1,…,Ain(R). А C a1 c1 a2 c1 a2 c2 А В C a1 b1 c1 a1 b2 c1 a2 b3 c1 a2 b4 c2

Операція обмеження (селекція) Нехай θ є одним з операторів порівняння: =, , , (набір операторів можна розширити). Атрибути А і В одного й того самого чи різних відношень називаються θ-порівнянними, якщо для будь-яких значень а є А і b є В результат операції аθb є визначеним (істинним або хибним). Набори атрибутів L= (А1,..., Аk) та М=(В1,...,Вn) називаються θ -порівнянними, якщо k=n i Ai є θ-порівнянним з Вi (і=1,2,...,k). Тоді вираз L θ М розуміють так: L θ М = (A1 θ В1) &...& (Аk θ Вk).

Операція обмеження (селекція) L θ M = ( A1 θ B1) &……& ( Ak θ Bk) R R [A = a2] А B C a2 b3 c1 a2 b4 c2 А В C a1 b1 c1 a1 b2 c1 a2 b3 c1 a2 b4 c2

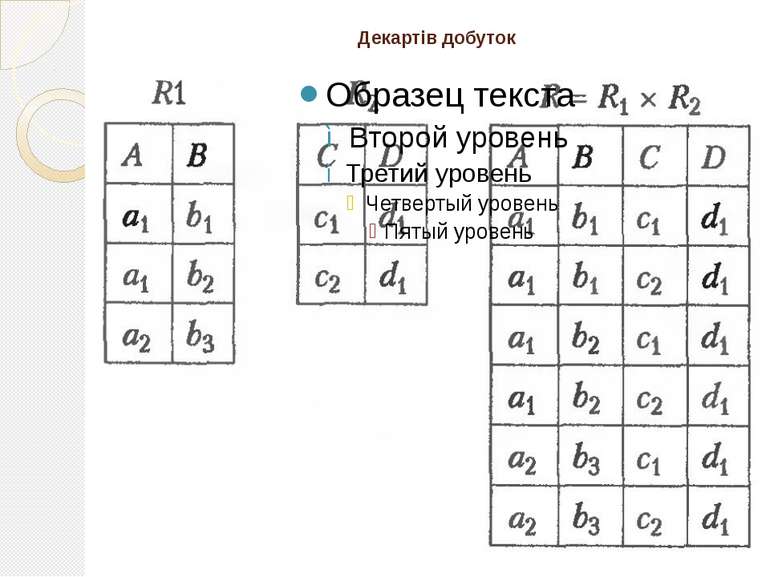
Декартів добуток Декартовим добутком реляційних відношень R і S зі схемами R(А1,А2,..., Ап) та S(В1, В2,..., Вт) відповідно, що позначається R ХS, називається відношення Q зі схемою Q(А1, А2,..., Ап, В1, В2,..., Вт), яке містить усі можливі з'єднання кортежів відношення R з кортежами відношення S: Q= R Х S ={(r,s)| r єR & s єS}. Операція комутативна й асоціативна.

Декартів добуток

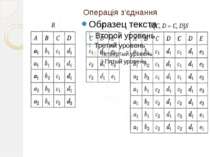
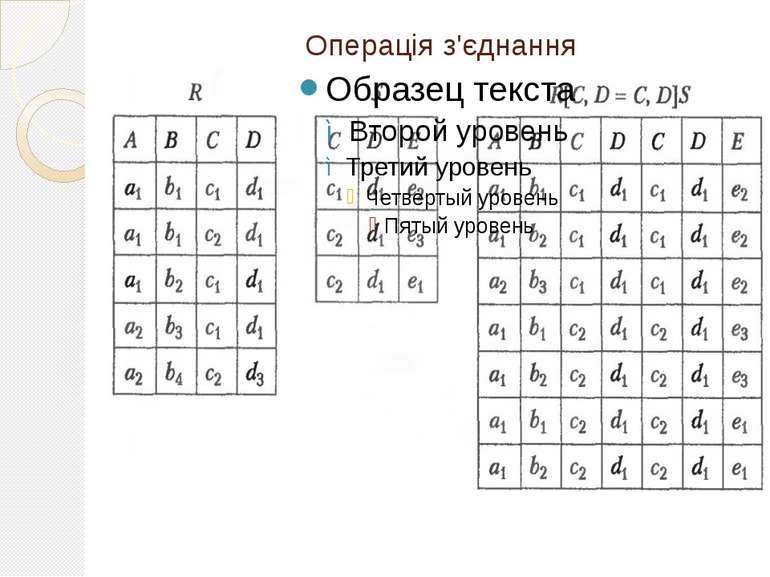
Операція з'єднання Нехай відношення R має схему R(L,М), а відношення S — схему S(N,Р). Нехай множини атрибутів М і N θ-порівнянні. З'єднанням (θ-з'єднанням), відношень R іS за умовою М θN (R[М θN]S), називається відношення Q(L, М, N. Р), кортежі якого можна отримати з'єднанням тих кортежів відношень R іS, на яких виконується умова М θN: Q=R[МθN]S={(r,s)|rєR & sєS&r[М] θs[N]}

Під час з'єднання атрибути, за якими виконується така операція, повторюються в кінцевому реляційному відношенні. Операція комутативна й асоціативна.

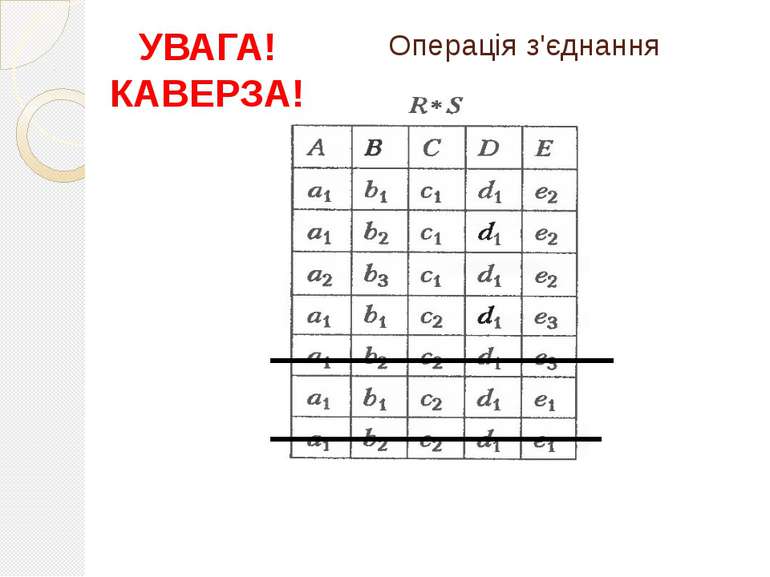
З'єднання за умовою З'єднання за умовою рівності називається еквіз'єднанням. З'єднання за умовою рівності, коли один з порівнюваних атрибутів (чи група порівнюваних атрибутів) видаляється з кінцевого відношення, називається природним з'єднанням ( * ). Наприклад, якщо задані відношення R(А, В, С, D) і S(С, D. Е), то в результаті виконання операції Q=R*S-отримаємо реляційне відношення Q(А, В, С, D, Е).

Серед операцій θ-з'єднання виділяють операцію напівз'єднання, за якої з результату видаляються всі атрибути одного з відношень, що з'єднуються.

Операція з'єднання

Операція з'єднання УВАГА! КАВЕРЗА!