Презентація на тему:
Показникова функція

Методична розробка теми: «Показникова функція» Учитель математики: Фетісова І.В. ЗОШ №3, м. Краматорськ 2010 рік

Зміст Показникова функція Показникові рівняння Показникові нерівності Типові задачі Тести Домашня контрольна робота

Показникова функція Графік Означення Властивості Зміст

Означення Показникова функція – це функція вида , де x – зміння, - задане число, >0, 1. Приклади: до теми

Властивості показникової функції Область визначення: всі дійсні числа Множина значень: всі додатні числа При > 1 функція зростає; при 0 < < 1 функція спадає. D(y) = R; E(y) = (0; + ∞); до теми

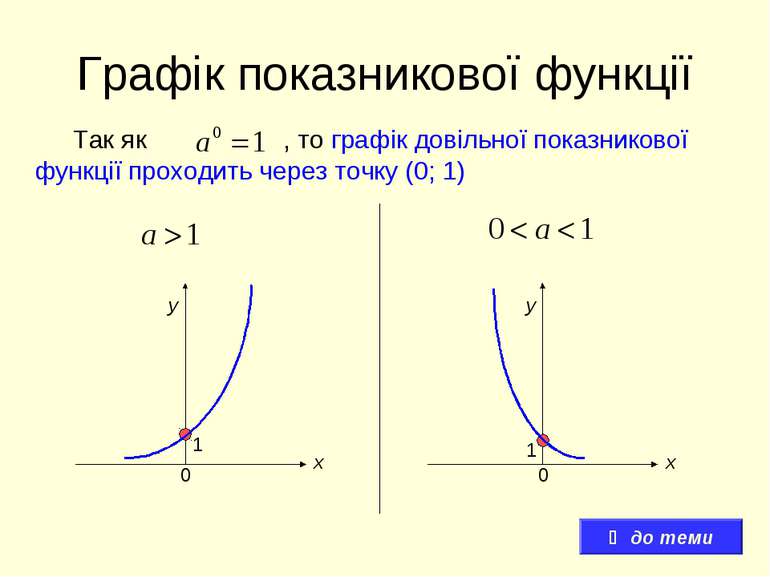
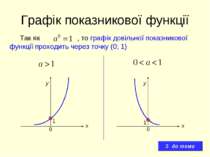
Графік показникової функції Так як , то графік довільної показникової функції проходить через точку (0; 1) 1 1 х х у у 0 0 до теми

Показникові рівняння Означення Найпростіші рівняння Способи розв’язання складних рівнянь Зміст

Означення Рівняння, в якому змінна знаходиться в показнику степені називається показниковим. Приклади: до теми

Найпростіші показникові рівняння – це рівняння вигляду Найпростіші показникові рівняння розв’язуються з використання властивостей степені. до теми

Способи розвязування складних показникових рівнянь Винесення за дужки степеня з найменьшим показником Заміна змінної Ділення на показникову функцію до теми

Винесення за дужки степеня з найменьшим показником Даний спосіб використовується, якщо виконуються дві умови: 1) Основи степені однакові; 2) коефіціенти перед змінною однакові На приклад: рішення

Заміна змінної При даному способі показникове рівняння зводиться до квадратного. Спосіб заміни зміної використовується, якщо показник однієї із степенів в 2 раза більше, ніж у другій. Наприклад: 3 2x – 4 · 3 х – 45 = 0 коефіціенти перед зміною протилежні Наприклад: 2 2 - х – 2 х – 1 =1 б) а) основи степенів однакові; рішення рішення

Ділення на показникову функцію Даний спосіб використовується, якщо основи степенів різні. а) в рівнянні виду ax = bx делимо на bx Наприклад: 2х = 5х | : 5x б) в рівнянні A a2x + B (ab)x + C b2x = 0 делимо на b2x. Наприклад: 3 25х - 8 15х + 5 9х = 0 | : 9x рішення рішення

Показникові нерівності Означення Найпростіші нерівності Решення нерівностей Зміст

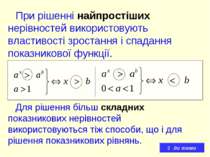
Означення Показникові нерівності – це нерівності, в яких невідоме міститься в показнику степені. Приклади: до теми

Найпрстіші показникові нерівності – це нерівності вида: де a > 0, a 1, b – довільне число. до теми

При рішенні найпростіших нерівностей використовують властивості зростання і спадання показникової функції. Для рішення більш складних показникових нерівностей використовуються тіж способи, що і для рішення показникових рівнянь. до теми

Типові задачі Показникова функція Показникові рівняння Показникові нерівності Зміст

Побудова графіка Порівняння чисел з використанням властивостей показникової функції Порівняння числа з 1 а) аналітичний спосіб; б) графичний спосіб. типові задачі

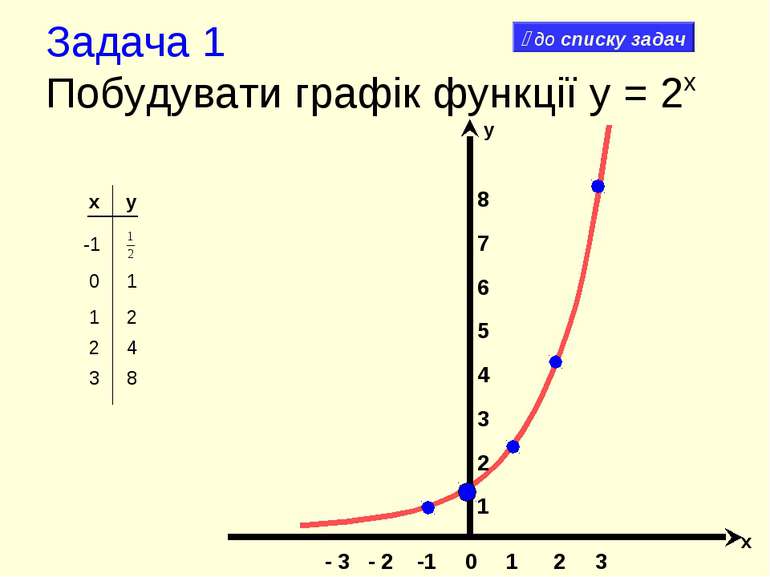
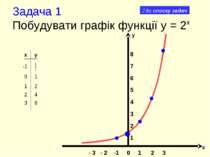
Задача 1 Побудувати графік функції y = 2x x y -1 8 7 6 5 4 3 2 1 - 3 - 2 -1 0 1 2 3 х у 3 8 2 4 1 2 0 1 до списку задач

Задача 2 Порівняти числа Рішення Відповідь: до списку задач

Задача 3 Порівняти число з 1. Рішення -5 < 0 Відповідь: до списку задач

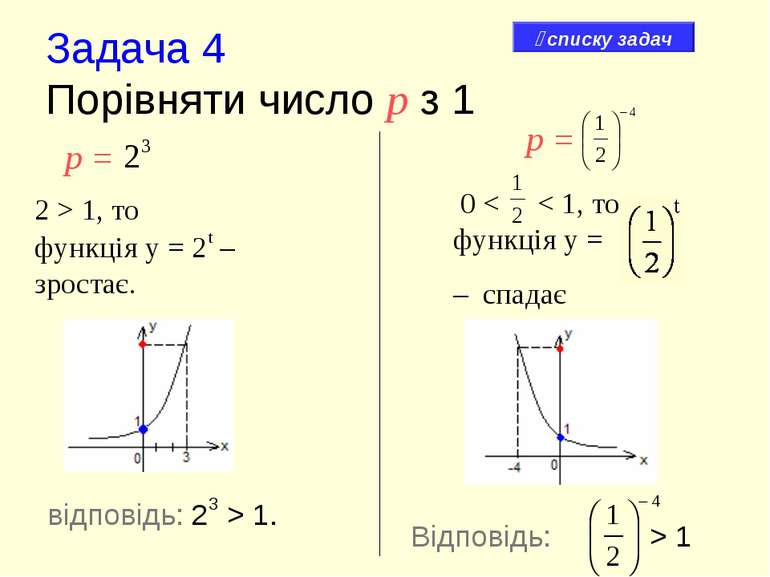
Задача 4 Порівняти число р з 1 р = 2 > 1, то функція у = 2t – зростає. 0 < < 1, то функція у = – спадає відповідь: 23 > 1. Відповідь: > 1 списку задач р =

Найпростіші показникові рівняння Рівняння, розвязуємі через винесення за дужки степені з найменшим показником Рівняння, розвязуємі заміною змінної випадок 1; випадок 2. Рівняння, розвязуємі діленням на показникову функцію випадок 1; випадок 2. типові задачи

Найпростіші показникові рівняння Відповідь: - 5,5. Відповідь: 0; 3. до списку задач

Винесення за дужки степеня з найменшим показником Відповідь: 5 x + 1 - (x - 2) = = x + 1 – x + 2 = 3 до списку задач до теорії

Заміна змінної (сл.1) основа степенів однакова, показник однієї з степенів в 2 раза більше, ніж у другій . 3 2x – 4 · 3 х – 45 = 0 t = 3x (t > 0) t 2 – 4t – 45 = 0 По т. Виета: t1· t 2 = - 45; t1+ t 2 =4 t1 = 9; t 2 = - 5 – сторонній корінь 3x = 9; 3x = 32; x = 2. Відповідь: 2 до списку задач до теорії

Заміна змінної (сл. 2) Основа степенів однакова, коефіціенти перед змінною протилежні. За т. Вієта: - Сторонній корінь Відповідь: 1 до списку задач До теорії

Ділення на показникову функцію Відповідь: 0 списку задач до теорії

Ділення на показникову функцію відповідь: 0; 1. списку задач до теорії

Найпростіші показникові нерівності Подвійні нерівності Нерівності, розвязуємі винесенням за дужки степіні з найменшим показником Нерівності, розвязуємі заміною змінної типові задачі

Найпростіші показникові нерівності до списку задач

Подвійні нерівності відповідь: (- 4; -1). 3 > 1, то до списку задач

Рішення показникових нерівностей Метод: Винесення за дужки степені з найменшим показником Відповідь: х >3 3 > 1, то : 10 списку задач

Рішення показникових нерівностей Метод: Заміна змінної Відповідь: х < -1. 3>1, то списку задач

Тести по темам: Показникова функція та її властивості Показникові рівняння Показникові нерівності зміст