Презентація на тему:
Лінійні рівняння з параметрами

Дослідницька робота учениці 10-го класу Солтисюк Юлії

Легко розв’язати таку нову задачу, яка схожа на розв’язану раніше. Однак задачі з параметрами часто не схожі одна на одну і за аналогією їх розв’язувати не можна. Розв’язування задач з параметрами розвиває абстрактне мислення, спонукає до пошукової діяльності, формує навички аналізу. Це важливо для математичного розвитку особистості – якості, що застосовується під час розв’язування прикладних задач з фізики, інформатики, економіки тощо.

Параметр (від грецького - той, що відміряє) - величина, значення якої слугують для встановлення відмінності між елементами деякої множини. Якщо в рівняння (нерівність, систему рівнянь, систему нерівностей) крім невідомих величин, входять числа, що позначені буквами, які хоч і не вказані, але вважаються відомими та заданими на деякій числовій множині, то вони називаються параметрами.

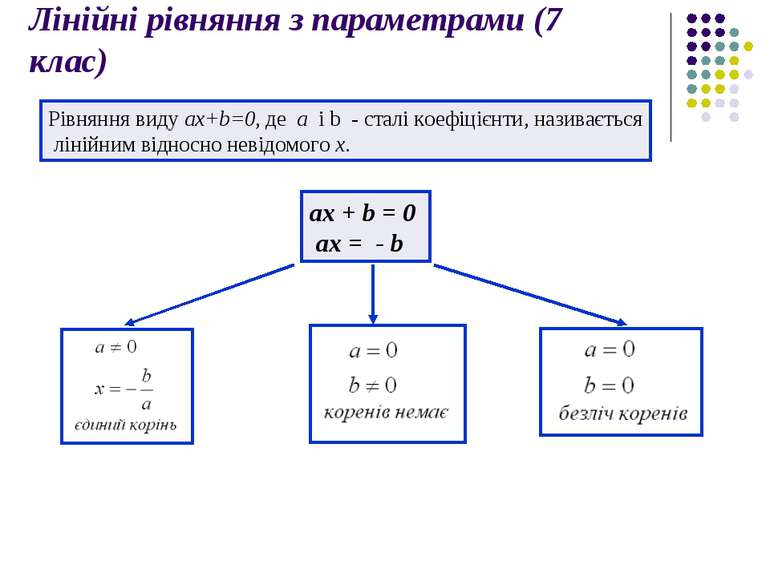
Лінійні рівняння з параметрами (7 клас) Рівняння виду ax+b=0, де a i b - сталі коефіцієнти, називається лінійним відносно невідомого x. ax + b = 0 ax = - b

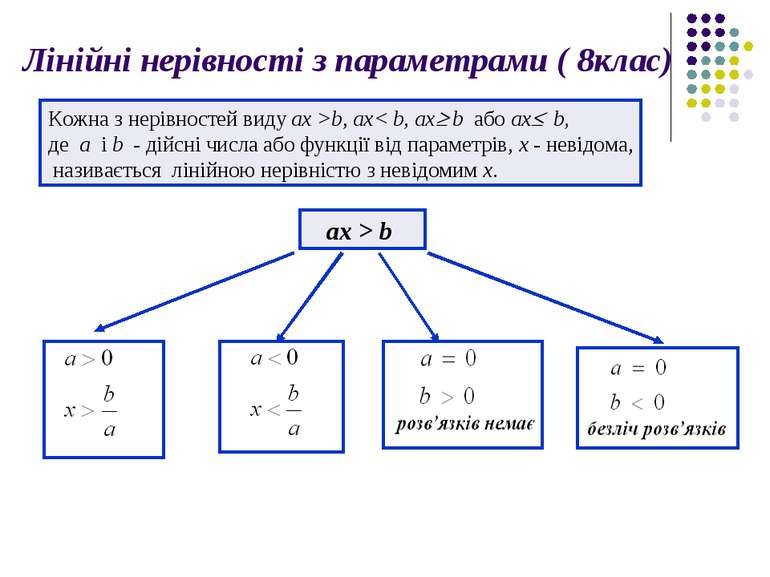
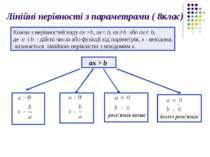
Лінійні нерівності з параметрами ( 8клас) Кожна з нерівностей виду ax >b, ax< b, ax b або ax b, де a i b - дійсні числа або функції від параметрів, x - невідома, називається лінійною нерівністю з невідомим x. ax > b

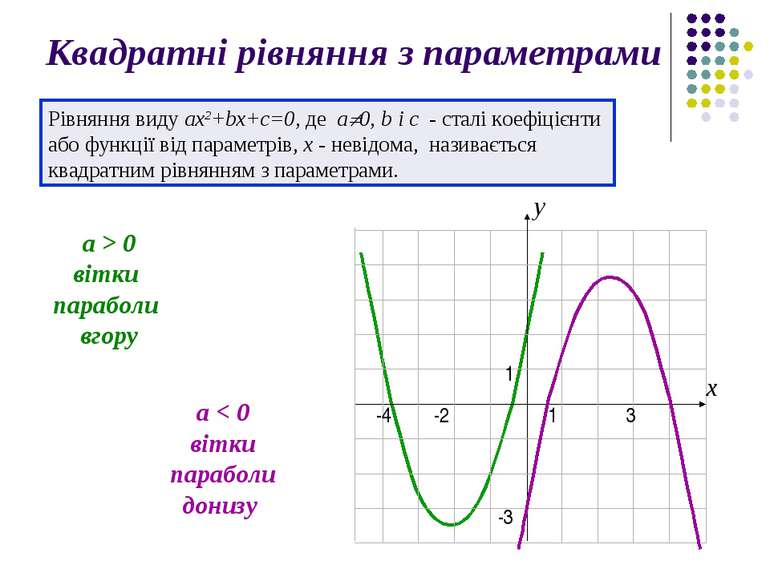
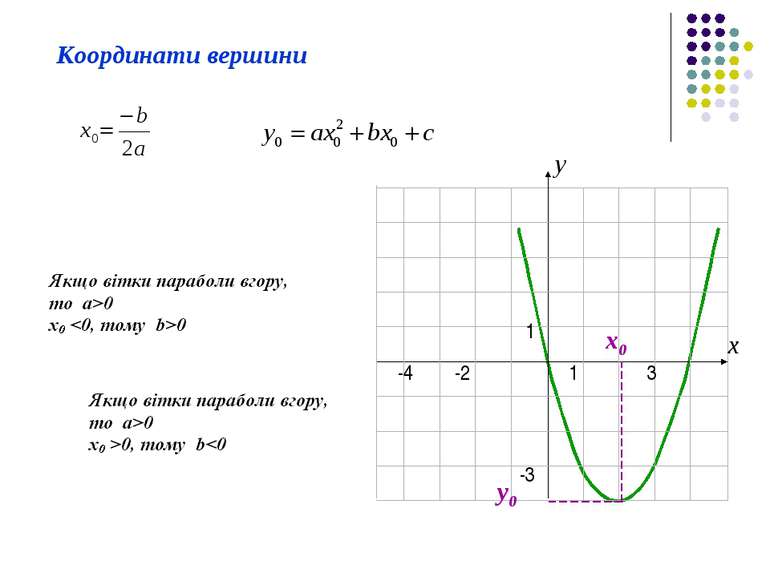
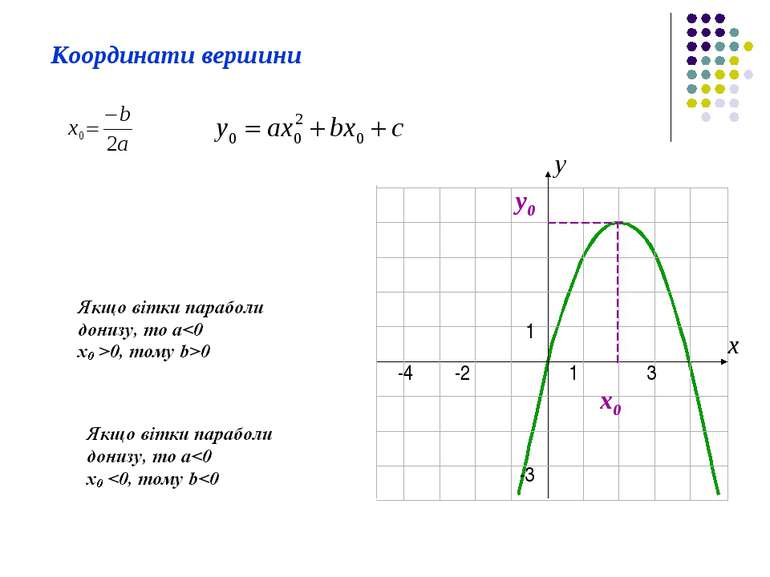
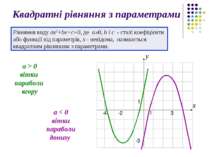
Квадратні рівняння з параметрами Рівняння виду ax2+bx+с=0, де a 0, b і с - сталі коефіцієнти або функції від параметрів, x - невідома, називається квадратним рівнянням з параметрами. a > 0 вітки параболи вгору a < 0 вітки параболи донизу

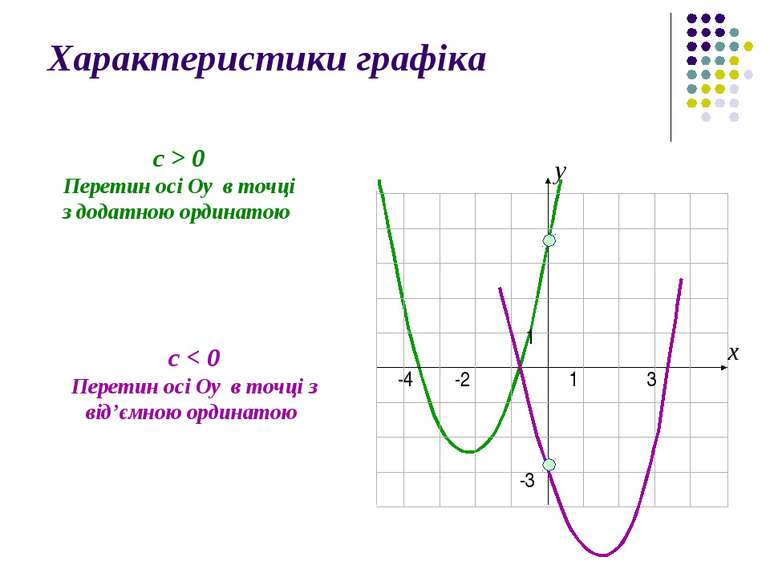
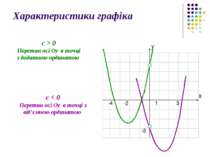
Характеристики графіка с > 0 Перетин осі Оу в точці з додатною ординатою с < 0 Перетин осі Оу в точці з від’ємною ординатою

Координати вершини x0 y0

Координати вершини x0 y0

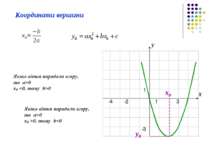
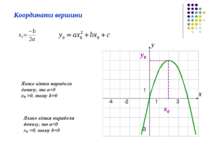
Графічний Аналітичний Графічно-аналітичний Розв’язати рівняння з параметрами означає знайти всі розв’язки цього рівняння для кожної допустимої системи значень параметрів або вказати при яких значеннях параметра рівняння розв’язків не має.

Аналітичний спосіб Приклад 1 При яких значеннях параметра а рівняння (а2-2а-3)х2- (а+1)х+5=0 має єдиний розв’язок? 1. Якщо а2-2а-3 = 0, то ми дістаємо лінійне рівняння х(а+1)=5. При а = 3 х = 1,25 При а = -1 – розв’язків не має. 2. При а -1, а 3 дискримінант D має дорівнювати нулю, тобто D= (a+1)2-20(a2-2a-3) =0 19a2- 42a – 61 = 0, Це можливо при а= -1 або а= 61/19 Але при а = -1 – розв’язків не має. Відповідь а=3 , а=

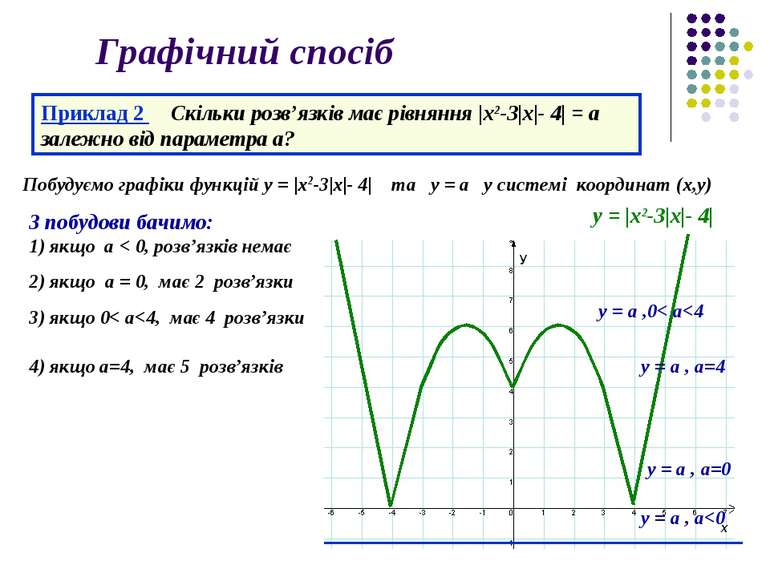
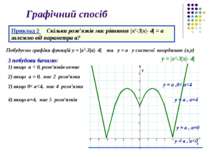
Графічний спосіб Приклад 2 Скільки розв’язків має рівняння |x2-3|х|- 4| = a залежно від параметра а? Побудуємо графіки функцій у = |x2-3|х|- 4| та у = a у системі координат (х,у) у = |x2-3|х|- 4| З побудови бачимо: 1) якщо a < 0, розв’язків немає у = a , a

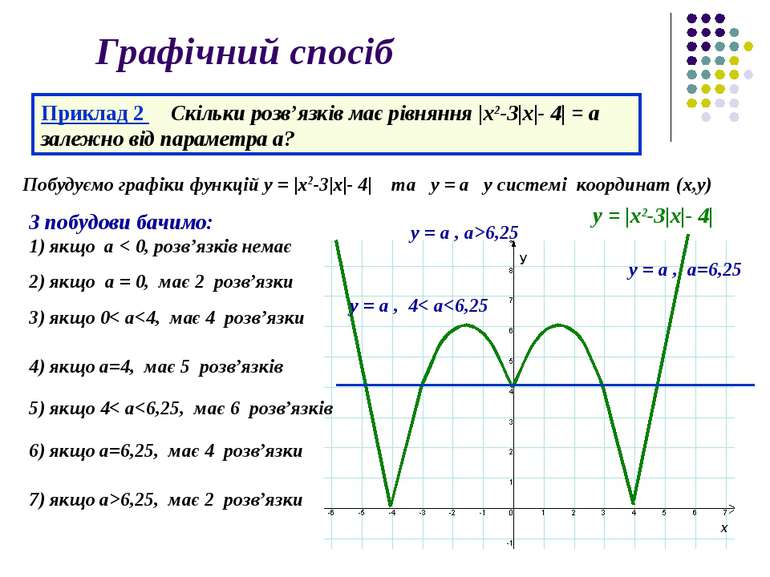
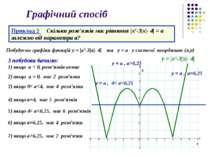
Графічний спосіб Приклад 2 Скільки розв’язків має рівняння |x2-3|х|- 4| = a залежно від параметра а? Побудуємо графіки функцій у = |x2-3|х|- 4| та у = a у системі координат (х,у) у = |x2-3|х|- 4| З побудови бачимо: 1) якщо a < 0, розв’язків немає у = a , a>6,25 2) якщо a = 0, має 2 розв’язки у = a , a=6,25 3) якщо 0< a

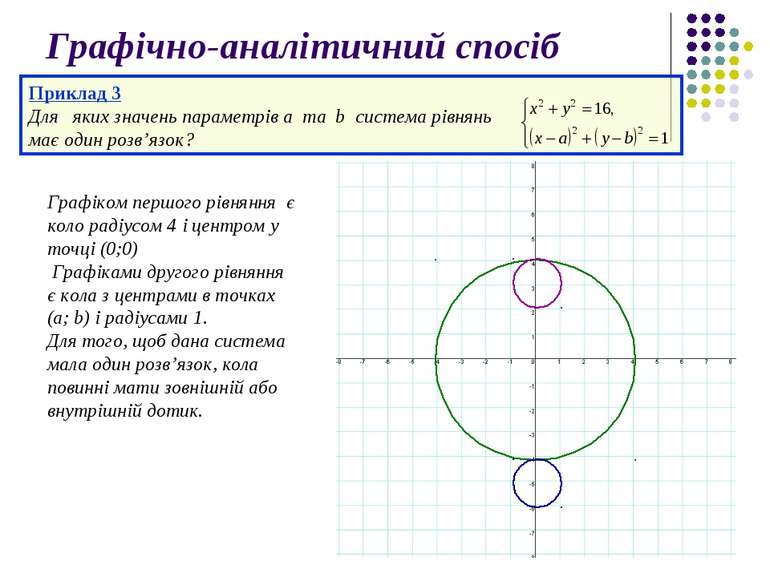
Графічно-аналітичний спосіб Приклад 3 Для яких значень параметрів а та b система рівнянь має один розв’язок? Графіком першого рівняння є коло радіусом 4 і центром у точці (0;0) Графіками другого рівняння є кола з центрами в точках (a; b) і радіусами 1. Для того, щоб дана система мала один розв’язок, кола повинні мати зовнішній або внутрішній дотик.

Графічно-аналітичний спосіб Приклад 3 Для яких значень параметрів а та b система рівнянь має один розв’язок? Геометричним місцем центрів кіл, що задовільняють умову задачі, є два концентричних кола з центрами в точці (0;0) і радіусами 3 і 5. Тому дана система рівнянь має один розв’язок для всіх значень a і b, що задовільняють сукупність:

Графічно-аналітичний спосіб Приклад 3 Для яких значень параметрів а та b система рівнянь має один розв’язок? Система має один розв’язок для всіх значень a і b таких, що :

15 13 11 9 + + + = 48

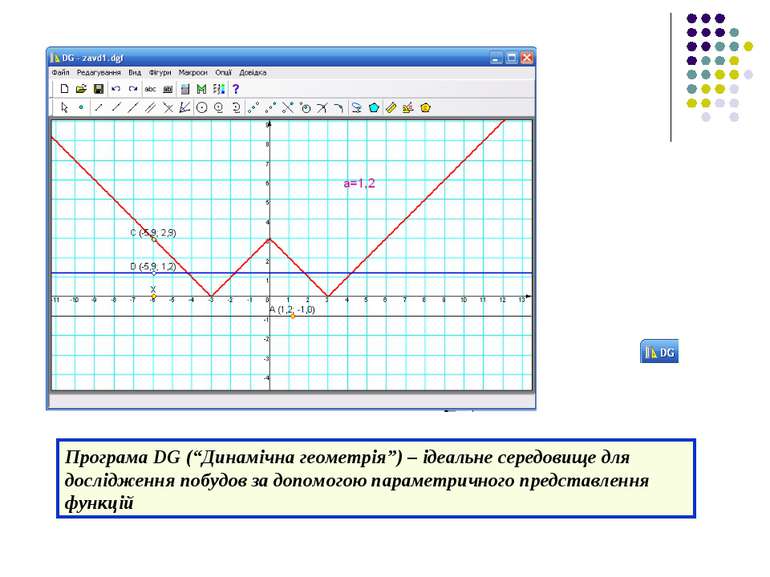
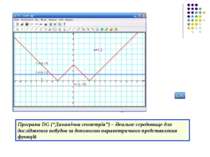
Програма DG (“Динамічна геометрія”) – ідеальне середовище для дослідження побудов за допомогою параметричного представлення функцій

Людина хотіла б володіти таким методом, який би давав можливість розв’язати будь-яку задачу. Над пошуком такого універсального методу міркував Рене Декарт, чіткіше ідею про досконалий метод сформулював Г. Лейбніц. “ Однак пошуки універсального, досконалого методу дали не більший ефект, ніж пошуки філософського каменя, який перетворює неблагородні метали в золото”, - писав Д. Пойя. Метою моєї роботи було дещо скромніше бажання продемонструвати три основні способи розв’язування задач з параметрами та переконати інших, що параметрами можна оперувати як числами, застосовуючи їх фіксованість, а з іншого боку – досліджувати їх “ступінь свободи”, тобто можливість змінюватись в межах заданих формул.