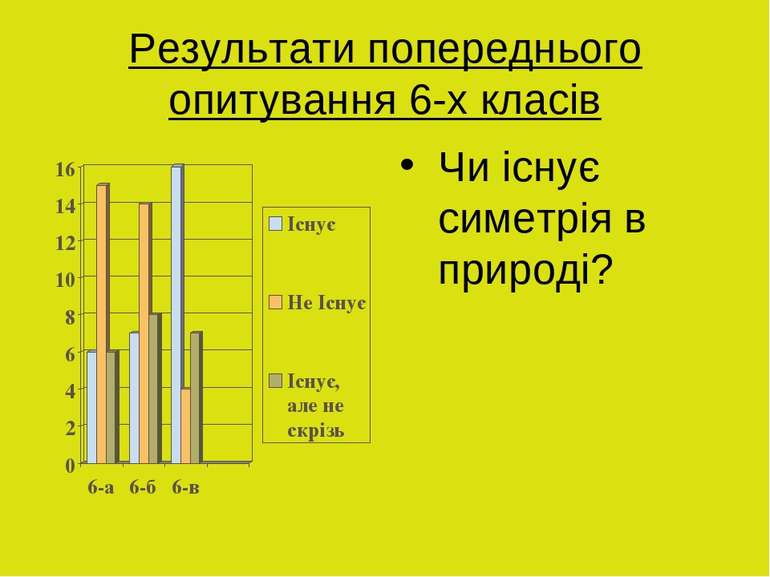
Презентація на тему:
Щр р

Симетрія відносно точки та прямої Тема уроку :

Симетрія-це слово грецького походження, означає спів розмірність

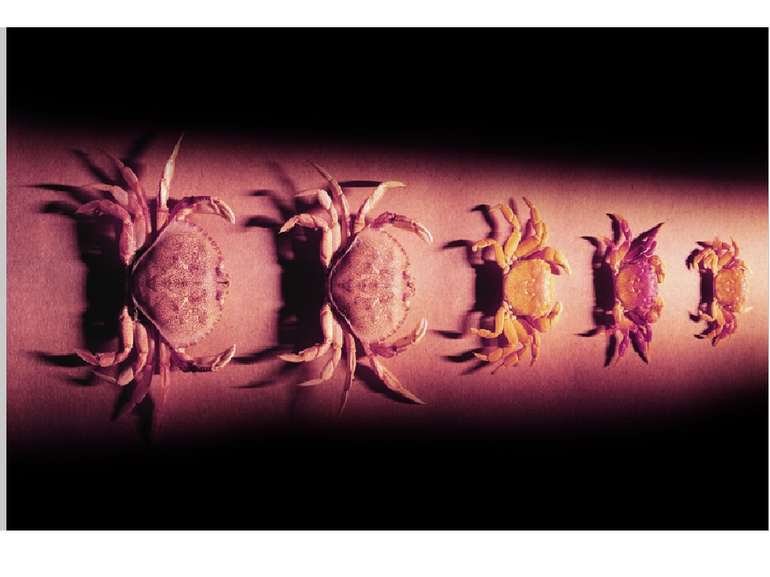
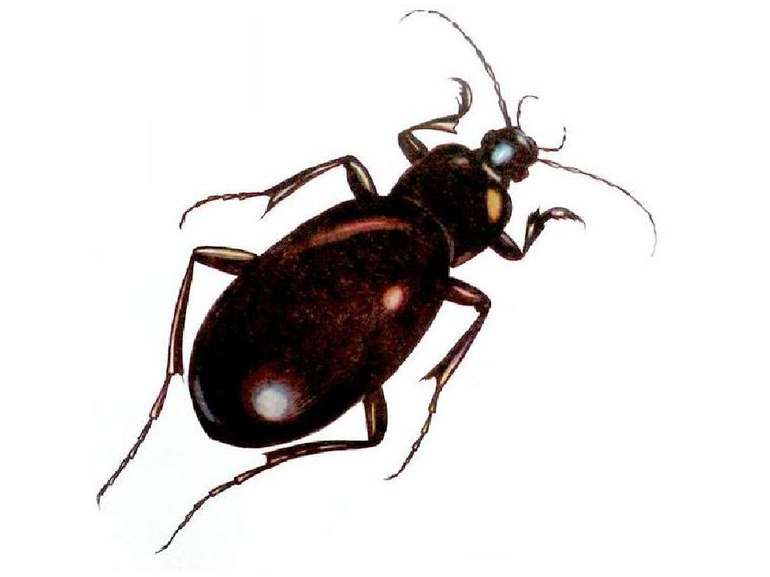
Симетрія-це властивість геометричної фігури Ф, що характеризує певну правильність форми Ф, незмінність її при дії рухів та дзеркальних відображень.

Чи є симетрія в природі?

Результати попереднього опитування 6-х класів Чи існує симетрія в природі?

Де шукатимемо симетрію? Серед тварин, птахів та риб. Серед дерев та квітів.

Серед тварин та людей Це вісь симетрії голови людини Це вісь симетрії голови тварини.

Світ рослин ? В рослинах симетрію не скрізь вдалося знайти

Майстерності конструювати за допомогою симетрії можна навчитися у природи

Перетворення симетрії в просторі Симетрія багатогранника. Її властивості є одночасно і прості, і складні; її способи виявлення – і одноразові, і багаторазові. Симетрія відносно площини називають ще дзеркальним відображенням..

фіксована точка довільна точка на площині Х О

Побудуємо промінь ХО Х О

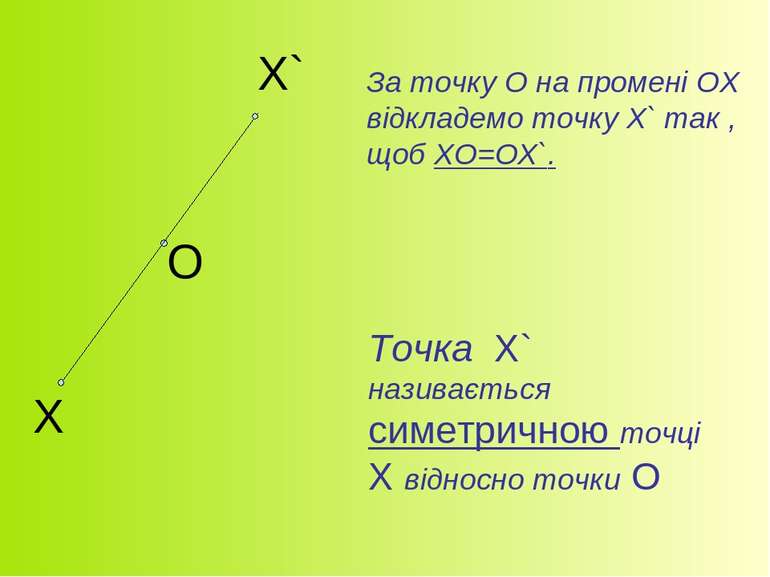
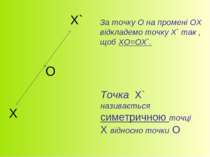
За точку О на промені ОХ відкладемо точку Х` так , щоб ХО=ОХ`. Точка Х` називається симетричною точці Х відносно точки О Х О Х`

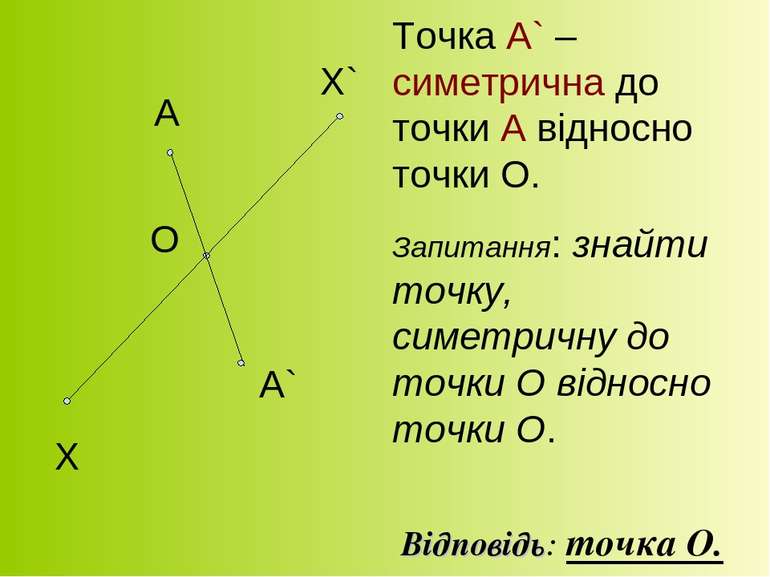
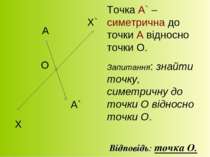
Х Х` А О А` Точка А` – симетрична до точки А відносно точки О. Запитання: знайти точку, симетричну до точки О відносно точки О. Відповідь: точка О.

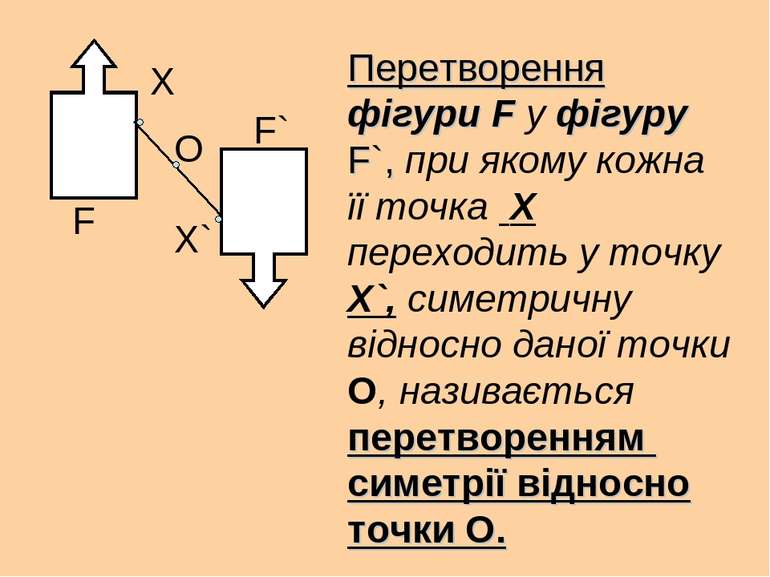
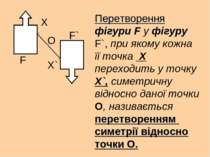
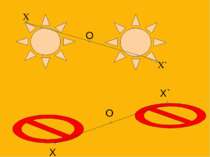
F F` X X` О Перетворення фігури F у фігуру F`, при якому кожна її точка X переходить у точку X`, симетричну відносно даної точки О, називається перетворенням симетрії відносно точки О.

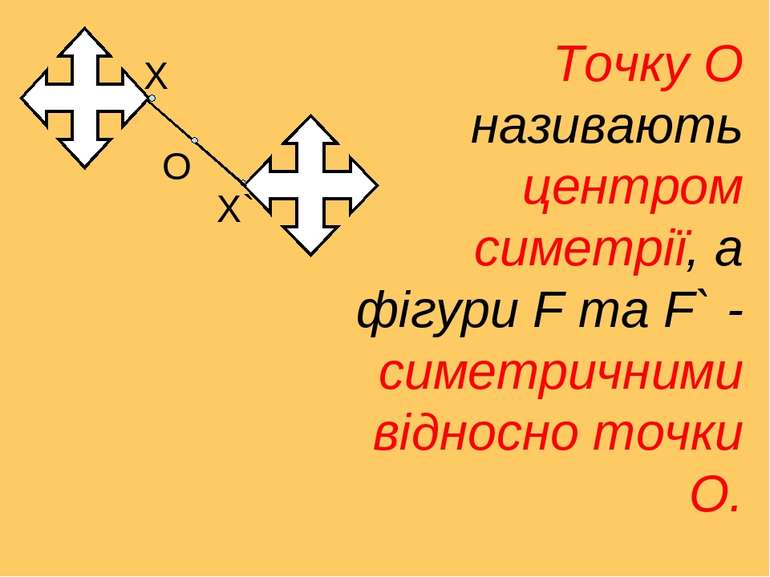
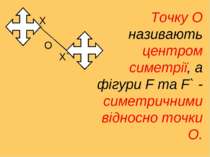
Х О Х` Точку О називають центром симетрії, а фігури F та F` - симетричними відносно точки О.

О О Х Х` X` X

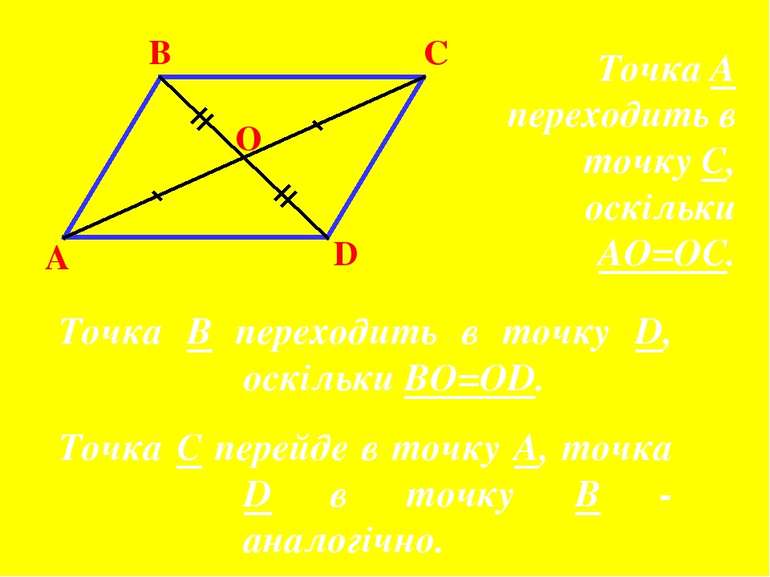
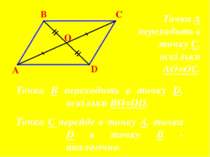
А В С D О Точка В переходить в точку D, оскільки ВО=ОD. Точка С перейде в точку А, точка D в точку В - аналогічно. Точка А переходить в точку С, оскільки АО=ОС.

ВИСНОВОК: перетворення симетрії відносно точки О переводить паралелограм у себе.

Якщо перетворення симетрії відносно точки О переводить фігуру F у себе, то вона називається центрально-симетричною, а точка О називається центром симетрії.

Отже, паралелограм є центрально-симетричною фігурою. Запитання: які ще приклади центрально-симетричних фігур ви знаєте ?

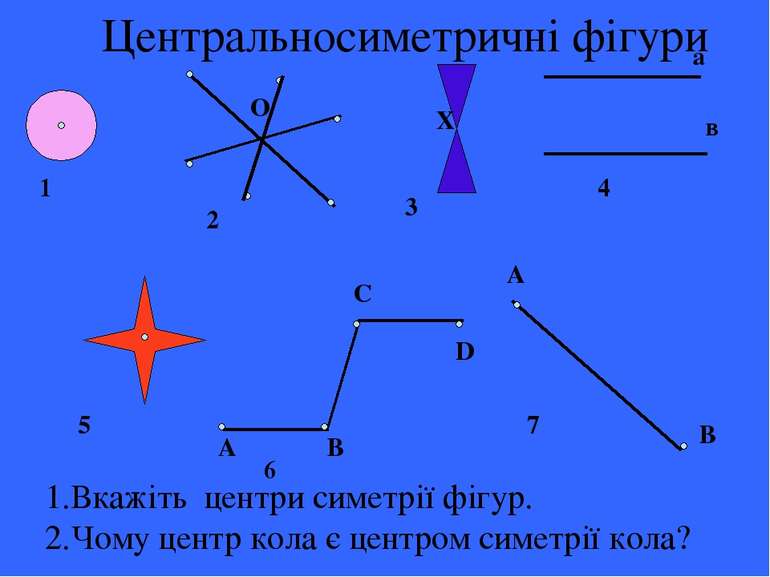
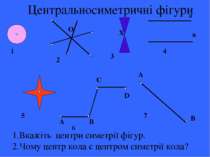
Центральносиметричні фігури а в А В С D А В О Х 1 4 2 3 5 6 7 1.Вкажіть центри симетрії фігур. 2.Чому центр кола є центром симетрії кола?

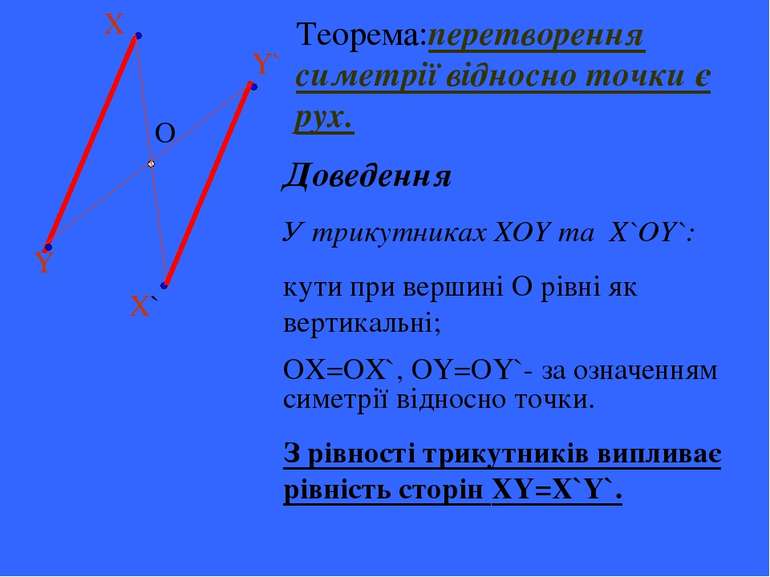
Y X X` Y` O Теорема:перетворення симетрії відносно точки є рух. Доведення У трикутниках XOY та X`OY`: кути при вершині О рівні як вертикальні; OX=OX`, OY=OY`- за означенням симетрії відносно точки. З рівності трикутників випливає рівність сторін XY=X`Y`.

Задача 11. Якою є фігура, симетрична відносно даної точки: а)до відрізка? б)до кута? в)до трикутника? (відрізок) (кут) (трикутник)

Симетрія відносно прямої X X` a Точка Х` називається симетричною точці Х відносно прямої a. а- фіксована пряма Х-довільна точка ХМ- перпендикуляр до прямої а ХМ=МХ` М

Запитання: де розташована точка, симетрична до точки Х, якщо Х лежить на прямій а ? а Х Точка, симетрична до Х, є сама точка Х.

Х Х` Перетворення фігури F у фігуру F`, при якому кожна її точка Х переходить у точку Х`, симетричну відносно даної прямої а, називається перетворенням симетрії відносно прямої а. При цьому фігури F та F` називаються симетричними відносно прямої а. F F` а

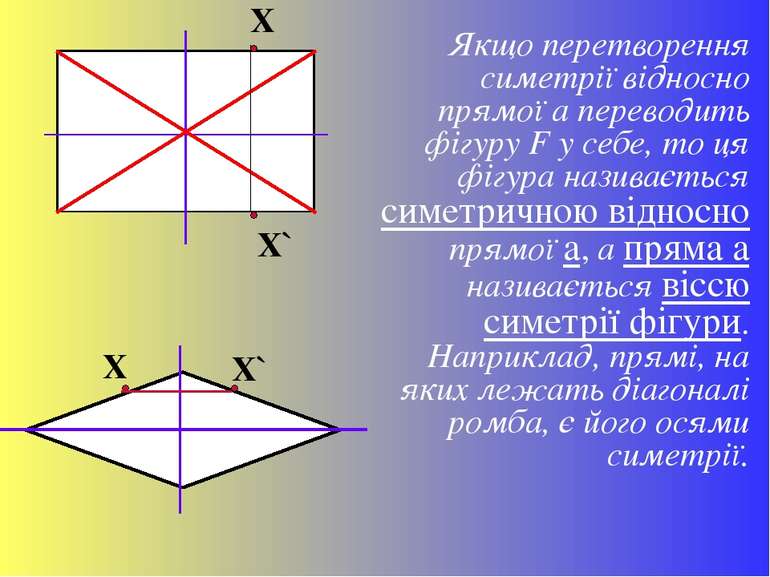
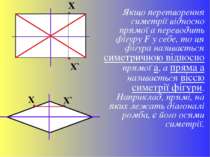
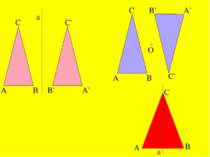
Якщо перетворення симетрії відносно прямої а переводить фігуру F у себе, то ця фігура називається симетричною відносно прямої а, а пряма а називається віссю симетрії фігури. Наприклад, прямі, на яких лежать діагоналі ромба, є його осями симетрії. X` X X X`

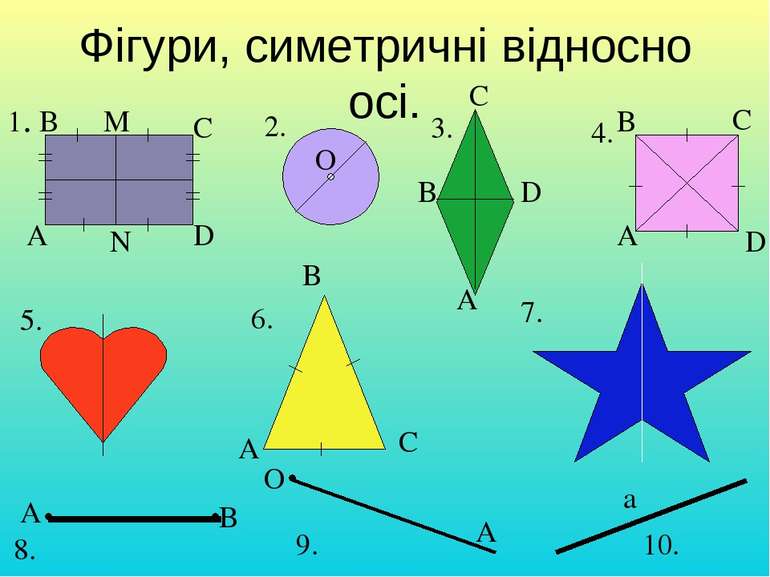
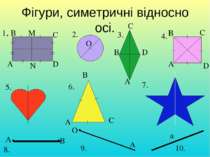
Фігури, симетричні відносно осі. 1. А В С D O A B C D A B C D A B C A B O A a 2. 3. 4. 5. 6. 7. 8. 9. 10. M N

Перетворення симетрії відносно прямої є рух Теорема:

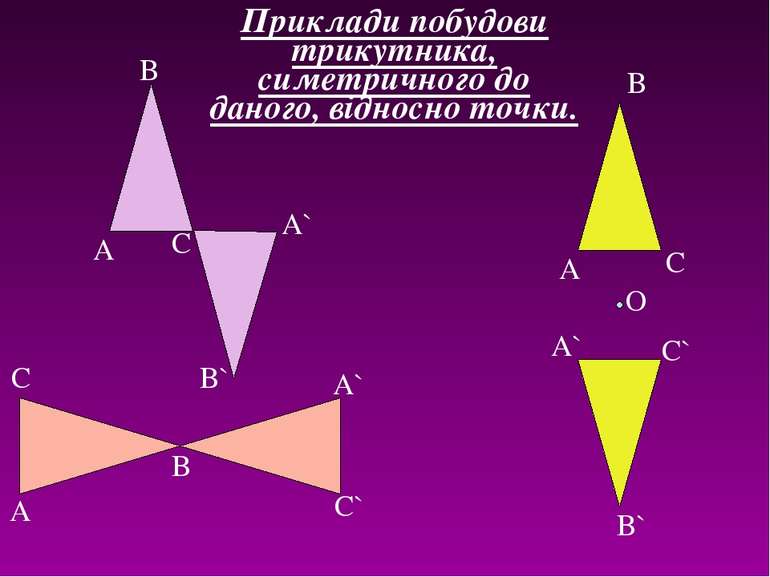
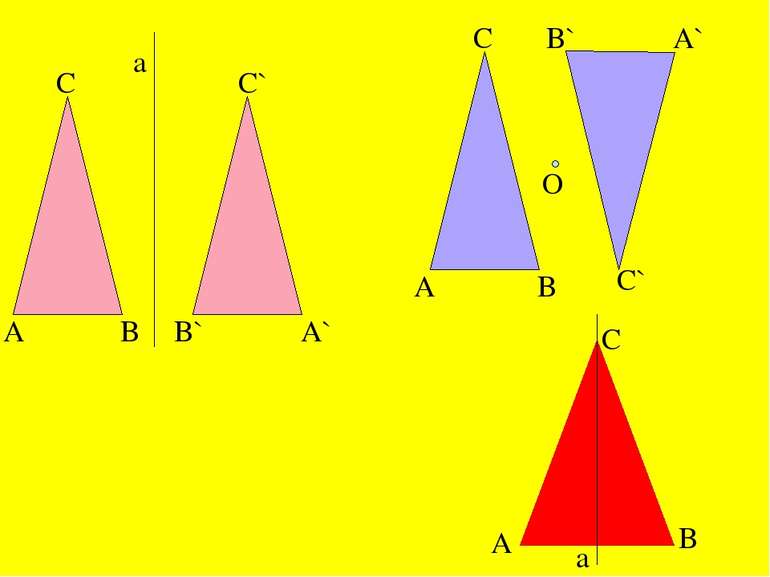
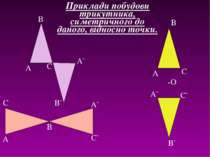
A B A B C O B` A` C` A C B C` A` C A` B` Приклади побудови трикутника, симетричного до даного, відносно точки.

A C B a B` A` C` A C O B B` A` C` A C B a

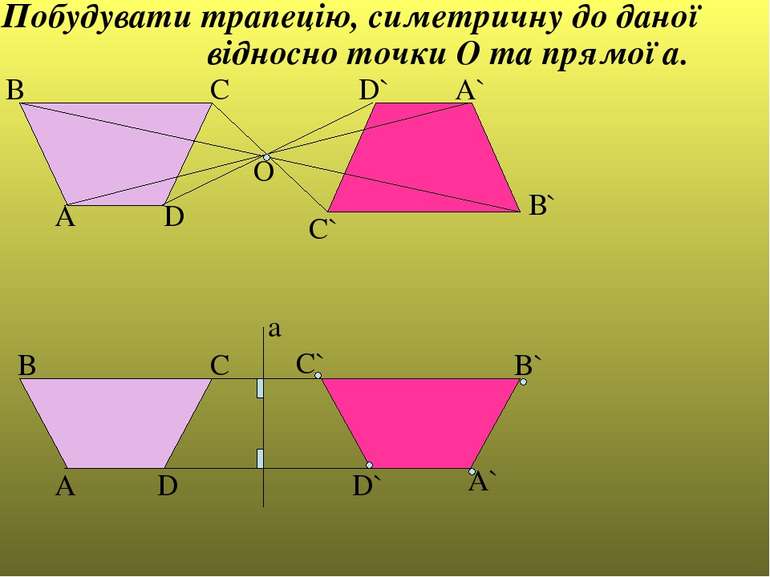
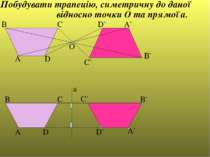
А В С D О А` В` C` D` A B C a A` D` D C` B` Побудувати трапецію, симетричну до даної відносно точки О та прямої а.

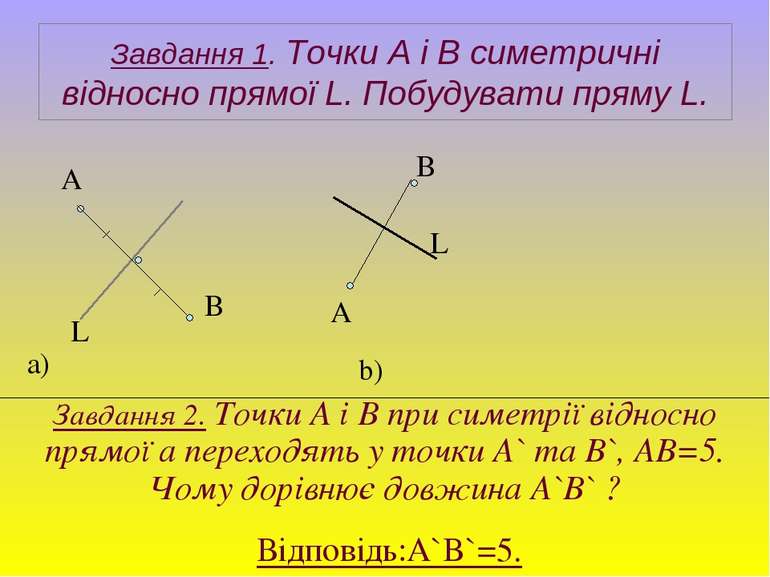
Завдання 1. Точки А і В симетричні відносно прямої L. Побудувати пряму L. А В L а) А В L b) Завдання 2. Точки А і В при симетрії відносно прямої а переходять у точки A` та B`, AB=5. Чому дорівнює довжина A`B` ? Відповідь:A`B`=5.

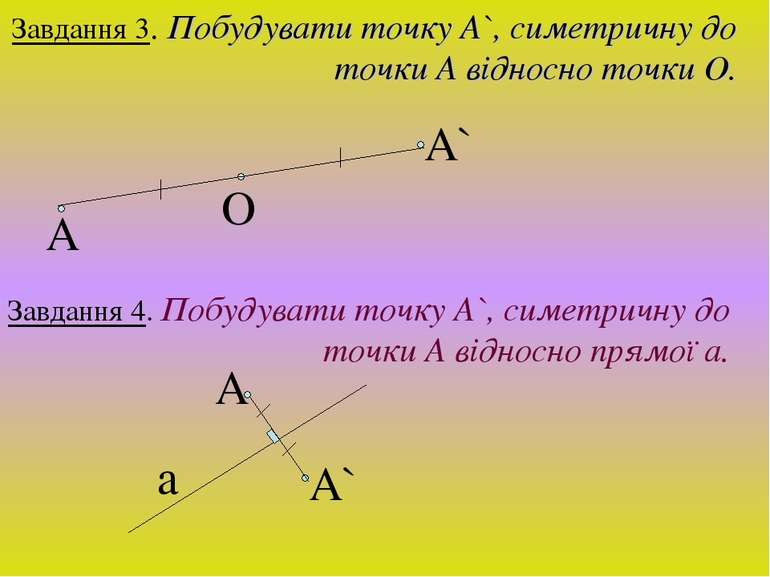
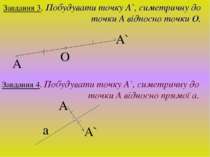
Завдання 3. Побудувати точку А`, симетричну до точки А відносно точки О. А О А` Завдання 4. Побудувати точку А`, симетричну до точки А відносно прямої а. А А` a

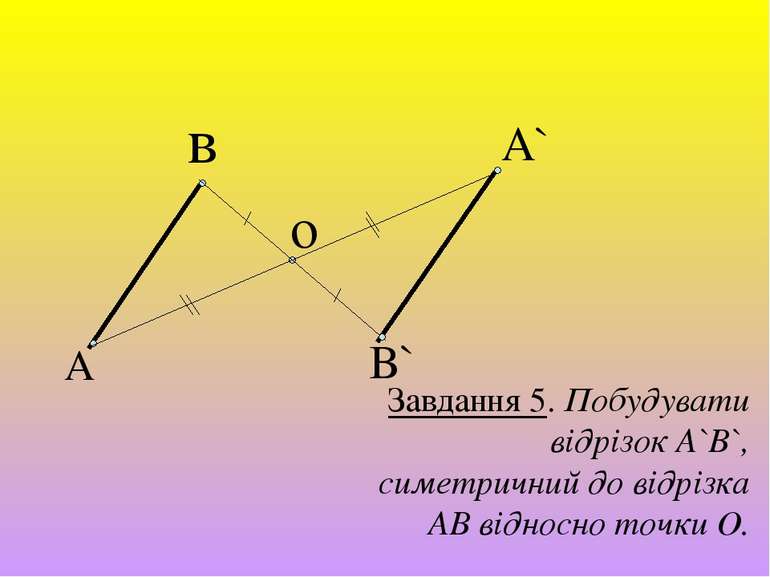
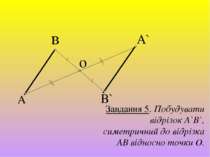
А в о B` A` Завдання 5. Побудувати відрізок А`B`, симетричний до відрізка АВ відносно точки О.

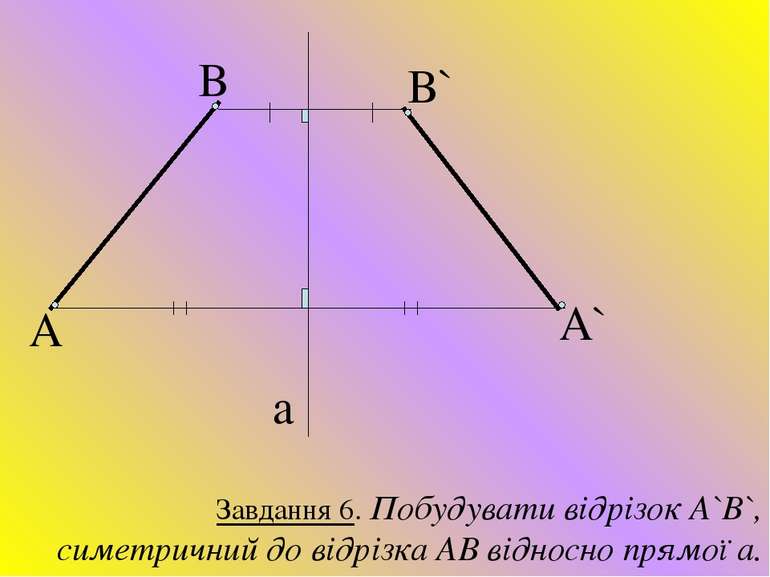
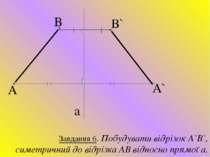
A B B` A` a Завдання 6. Побудувати відрізок A`B`, симетричний до відрізка АВ відносно прямої а.

Завдання додому: пункт 85, 86. № 19, 12.