Презентація на тему:
Тести з алгебри

План уроку № з/п Назва етапу Час хв. Методи та прийоми 1. Організаційний 1 Привітання 2. Ознайомлення з планом уроку 2. Перевірка домашнього завдання 2 1.Бесіда. 2. Взаємоперевірка д/з. 3. Актуалізація опорних знань 10 Інтелектуальна розминка “Естафета” 4. Мотивація навчальної діяльності. Повідомлення теми, мети, епіграфу уроку 2 Інтерв'ю 5. Засвоєння навичок 20 1.Комп'ютерна презентація. 2. Робота консультантів 6. Побудова графіків з модулем. Розв'язування рівнянь з параметром. 6 Робота на мультимедійній дошці. № 294г. Розв'язати рівняння ||x|-2|=a 7. Підсумок уроку 3 Рефлексія 8. Домашнє завдання 1 §2 п.10, Р.А №282(а-в); Р.Б №285 (б-г); Р.В №292(а)- виправити помилку; №294 (а) Додаткове завдання: розшифрувати орнамент (індивід. картки).

Картка оцінювання

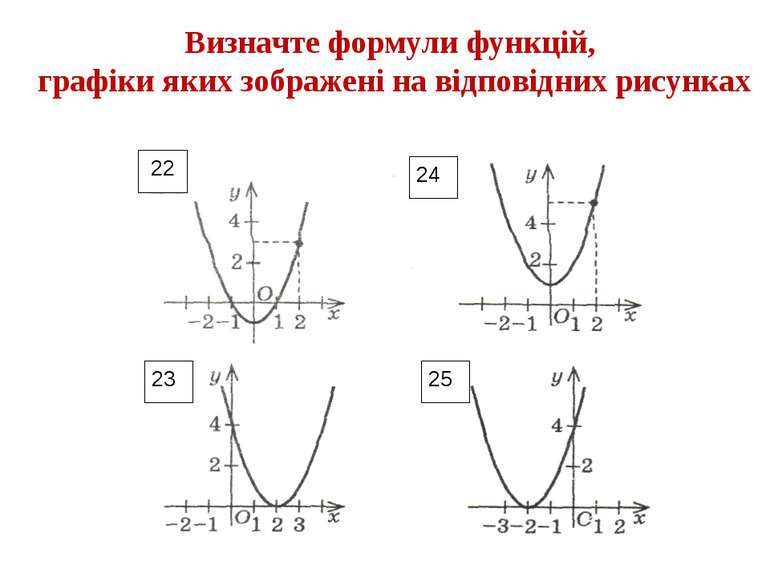
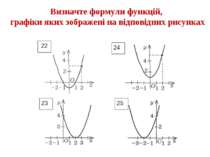
1. Горизонтальна вісь називається…, вертикальна - … 2. Разом вони утворюють …, вона має ще назву … 3. Площина, на якій вона зображена, називається … площиною, що має … чверті. 4. Область визначення позначається …, знаходимо її на осі … 5. Область значень позначається …, знаходимо її на осі… 6. Графік парної функції… відносно осі… Вставте пропущені слова

7. Графік непарної функції … відносно… 8. Графіком функції у=х2 є … 9. Функція у=kх називається … 10. Функція називається … 11.Графіком функції є…

Графічний тренінг За графіком лінійної функції визначте правильне твердження:

За графіком функції у = f(x) визначте неправильне твердження:

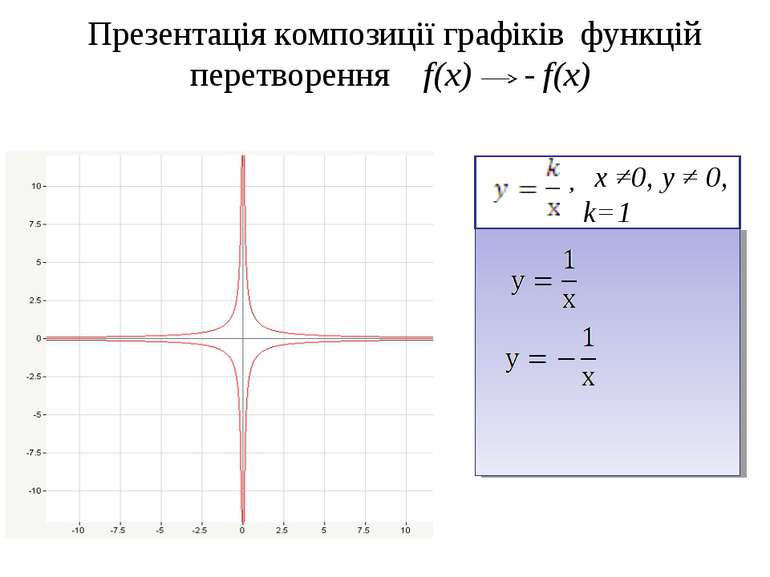
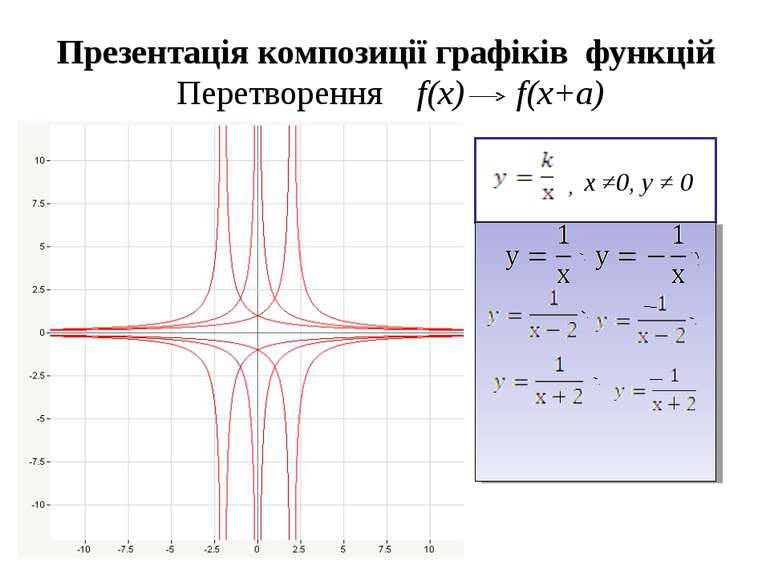
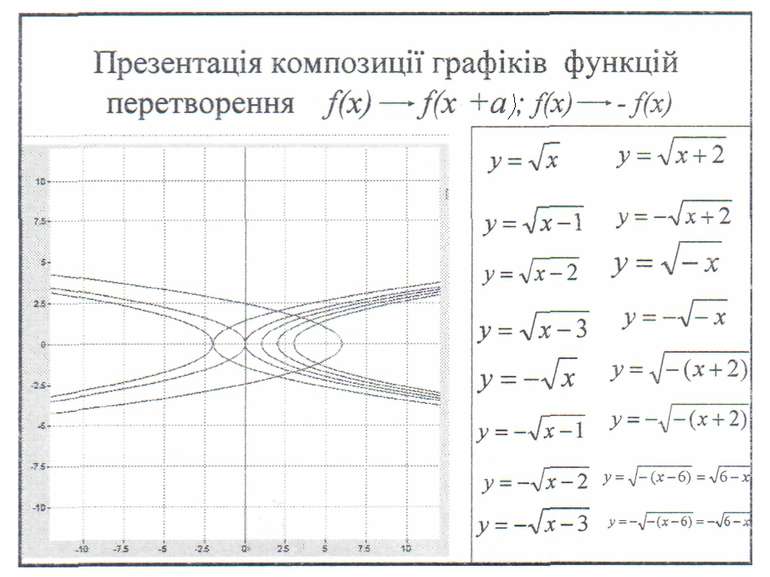
Вставте пропущені слова 20.Якщо f(x) перетворюється у f(x)+а, то графік рухається вздовж осі … на а одиниць …, якщо а>0 і на а одиниць…, якщо а0, і на а одиниць…, якщо а

25 Визначте формули функцій, графіки яких зображені на відповідних рисунках 24 22 23

Інтерв’ю Як ви вважаєте, чи достатньо оволодіти лише теоретичними знаннями про елементарні функції?

Тема уроку Розв’язування вправ на перетворення графіків функцій

Мета уроку удосконалювати навички перетворення графіків функцій: f(x) f(x)+a; f(x) f(x+a); f(x) k f(x); f(x) - f(x) та побудови графіків функцій з використанням зазначених перетворень графіків; вчити розпізнавати функцію за її графіком; сприяти формуванню пізнавальної компетенції та особистісному зростанню учнів; розвивати уяву, математичну культуру мови, творче, асоціативне та критичне мислення; виховувати увагу, активність, естетичний смак, почуття єдності та відповідальності за спільну справу.

Епіграф уроку Не достатньо мати лише добрий розум, головне - це раціонально застосовувати його Р. Декарт

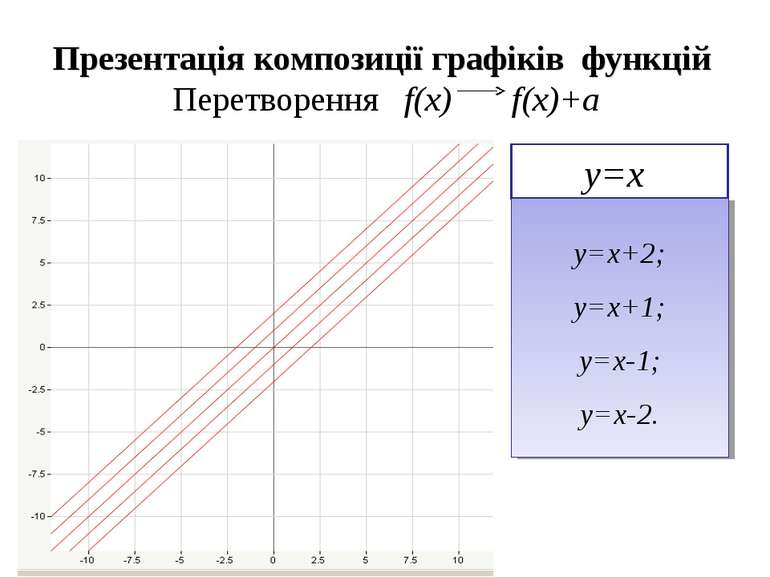
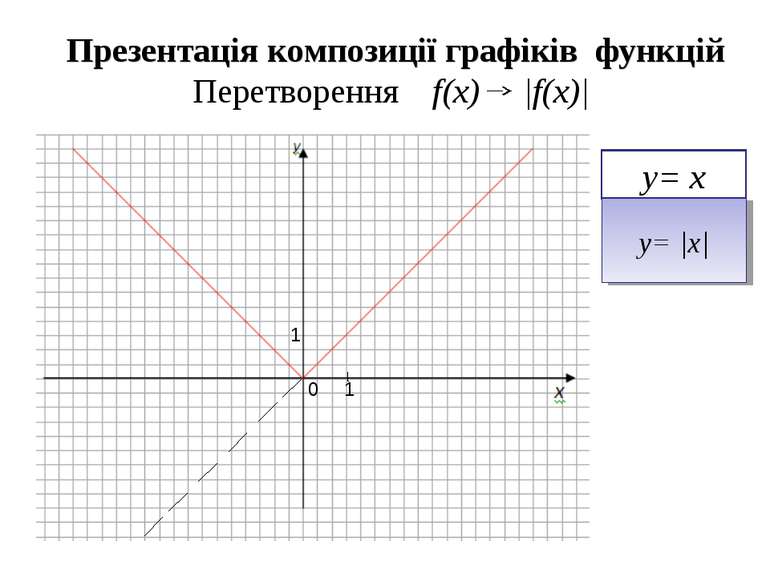
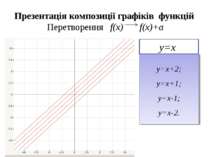
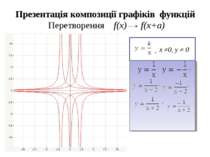
Презентація композиції графіків функцій Перетворення f(x) f(x)+a у=х у=х+2; у=х+1; у=х-1; у=х-2.

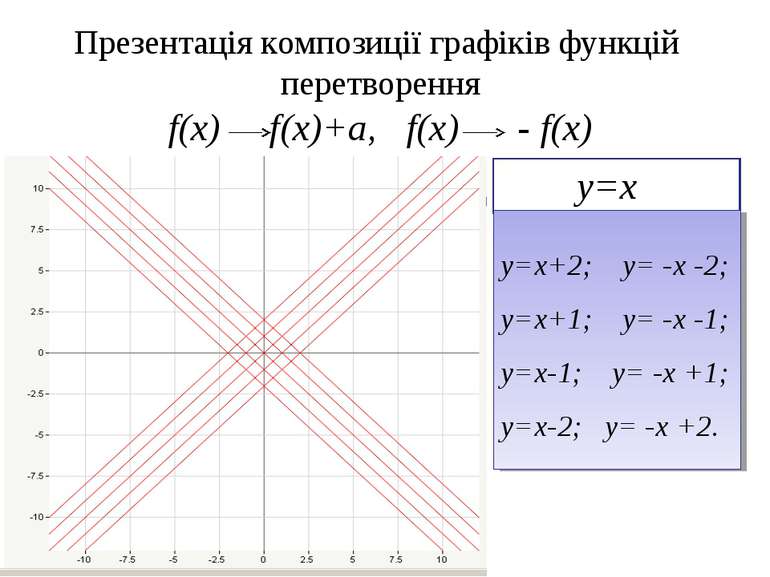
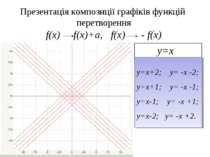
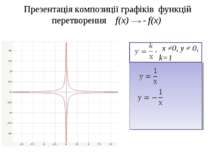
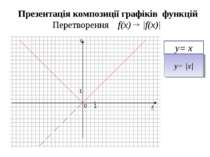
Презентація композиції графіків функцій перетворення f(x) f(x)+a, f(x) - f(x) у=х у=х+2; у= -х -2; у=х+1; у= -х -1; у=х-1; у= -х +1; у=х-2; у= -х +2.

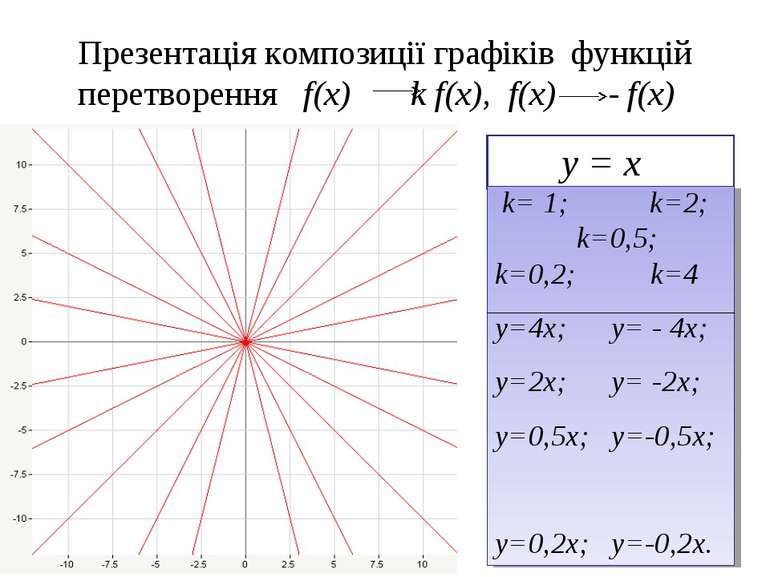
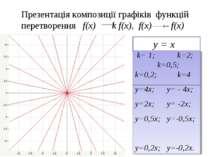
Презентація композиції графіків функцій перетворення f(x) k f(x), f(x) - f(x) у = х k= 1; k=2; k=0,5; k=0,2; k=4 у=4х; у= - 4х; у=2х; у= -2х; у=0,5х; у=-0,5х; у=0,2х; у=-0,2х.

Презентація композиції графіків функцій перетворення f(x) - f(x) х ≠0, у ≠ 0, k=1

Презентація композиції графіків функцій Перетворення f(x) f(x+a) х ≠0, у ≠ 0

графіки

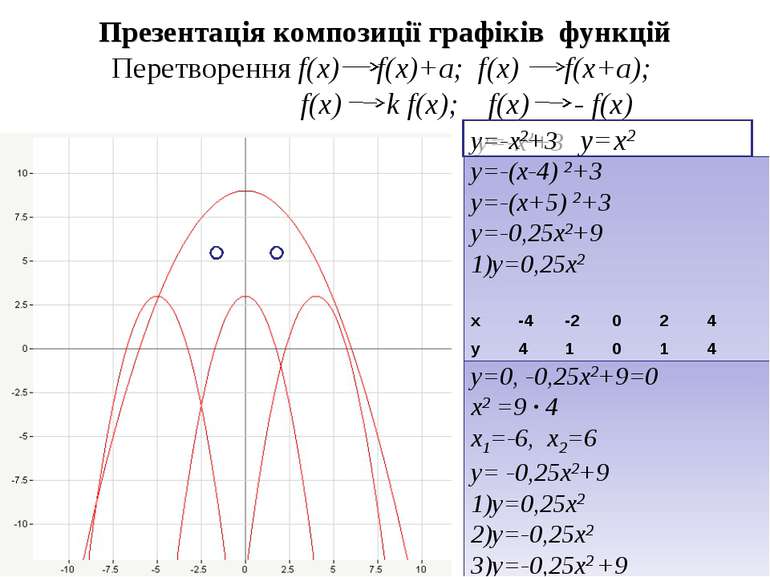
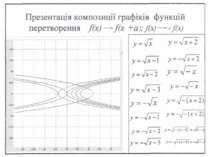
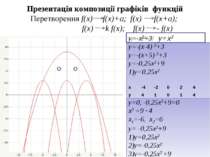
Презентація композиції графіків функцій Перетворення f(x) f(x)+a; f(x) f(x+a); f(x) k f(x); f(x) - f(x) у=х2 у=-х2+3 у=-(х-4) 2+3 у=-(х+5) 2+3 у=-0,25х2+9 у=0,25х2 у=0, -0,25х2+9=0 х2 =9 · 4 х1=-6, х2=6 у= -0,25х2+9 у=0,25х2 у=-0,25x2 у=-0,25x2 +9 х -4 -2 0 2 4 у 4 1 0 1 4

Презентація композиції графіків функцій Перетворення f(x) |f(x)| y= x y= |x| 0 1 1

1.Побудова графіків з модулем: робота на мультимедійній дошці №294г. Побудувати графік функції у=||x|-2|. 2. Розв'язування рівнянь з параметром: для яких а рівняння ||x|-2|=а має корені і скільки?

фото

фото

Підсумок уроку Чи була досягнута зазначена мета уроку? Чи сподобався вам урок? Чому? Ваші пропозиції щодо подальшої співпраці. Виставлення оцінок за урок.

§2, п.10, Р.А. №282 (а-в), Р.Б. №285 (б-г), Р.В. №292(а) виправити помилку, №294(а). Додаткове завдання: Розшифрувати «Орнамент»

Дякую за співпрацю !