Презентація на тему:
З досвіду роботи вчителів математики та фізики

З досвіду роботи вчителів математики та фізики Вілєгжаніної Т.В. та Долінко О.В.

Загальношкільна проблема Забезпечення якісної освіти учнів закладу в умовах особистісно-зорієнтованого і компетентнісного навчання

Проблема ШМО вчителів математики, фізики та інформатики Формування математичних, фізичних , інформатичних компетентностей.

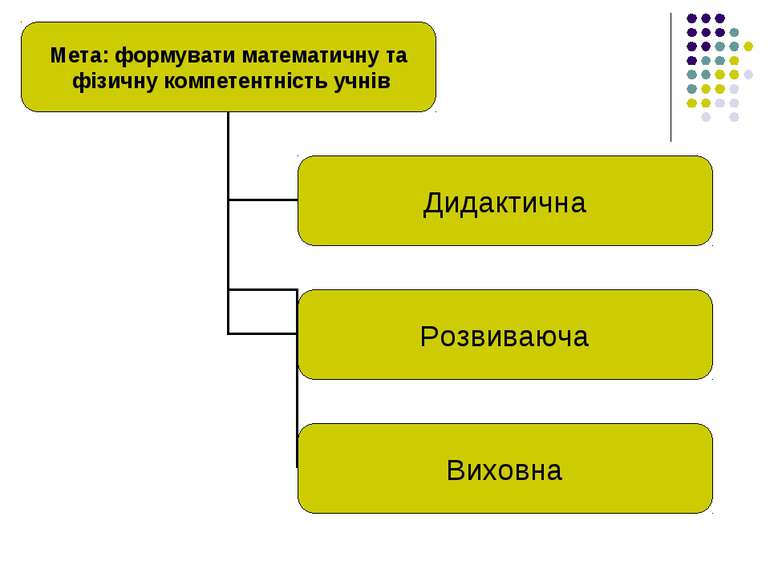
З точки зору компетентнісно зорієнтованого підходу до організації навчально-виховного процесу, зміст математичної освіти має бути спрямований на досягнення таких цілей: інтелектуальний розвиток учнів, формуваня видів мислення, характерних для математичної діяльності і необхідних людині для повноцінного життя у суспільстві; оволодіння прийомами математичної діяльності, які необхідні у вивченні суміжних предметів для продовження навчання та в практичній діяльності; формування уявлень про математику як форму опису і метод пізнанння дійсності; виховання учнів у процесі навчання математики; формування позитивного ставлення та інтересу до математики.

Математичні та фізичні компетентності процедурна компетентність – уміння розв’язувати типові математичні та фізичні задачі. логічна компетентність – володіння дедуктивним методом доведення та спростування тверджень. технологічна компетентність – володіння сучасними математичними пакетами. дослідницька компетентність – володіння методами дослідження практичних та прикладних задач математичними методами.

Компоненти компетентностей мотиваційний – внутрішня мотивація, інтерес; змістовний – комплекс математичних знань, умінь та навичок; дійовий – навички навчальної праці (самостійність, самооцінка, самоконтроль).

Інтегрований урок — це в основному урок систематизації та узагальнення знань, умінь і навичок учнів, його структурою є: повідомлення теми, цілей та зав дань уроку; мотивація навчальної діяльності учнів; актуаліза ція та корекція опорних знань; повторення й аналіз основних фактів, подій, явищ; творче перенесення знань і навичок учнів у нові ситуації; узагальнення та системати зація знань учнів, основних ідей та наукових теорій, предметів, що є складо вими інтегрованого уроку. Завдання вчителя полягає в тому, щоб встановлювати міжмред метні зв'язки для розробки інтегрованих уроків та їх проведення. Визначення теми уроку, обговорення його змісту й методики проведення, складання плану вимага ють творчого підходу та комбінованого погляду на тему. Інтегровані уроки цілеспрямо вані й певною мірою знімають кордони предметного викладання, допомага ють учням емоційно й системно сприймати запропонований матеріал, реалізу ють принципи єдності навчання і виховання, наочності, доступності, самостійно сті, активності – учні вчаться співпрацювати.

Гармонічні коливання Інтегрований урок математики і фізики в 10 класі

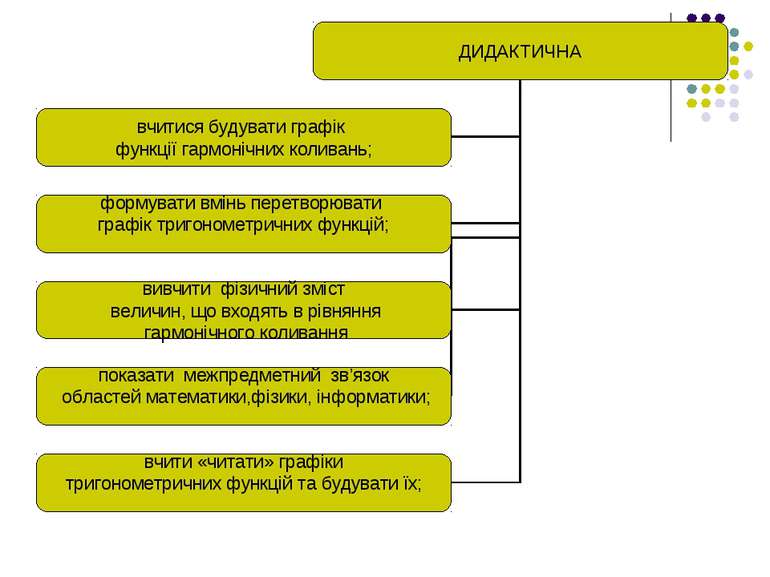
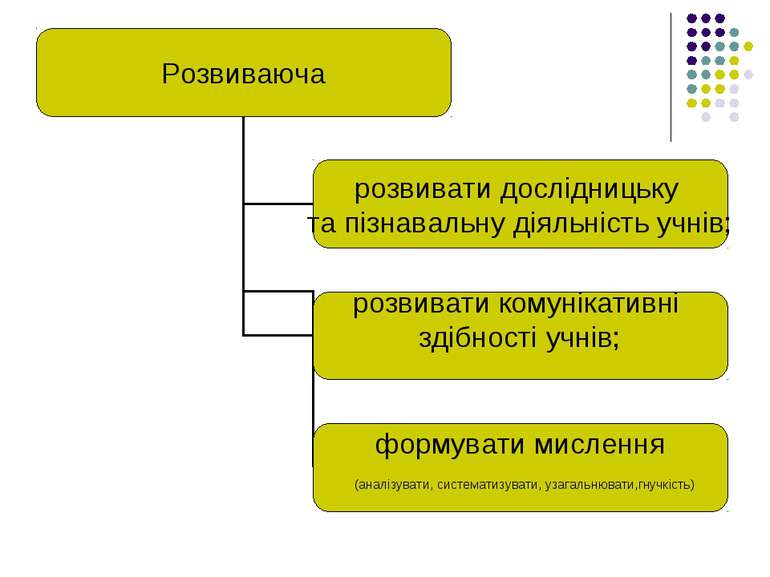
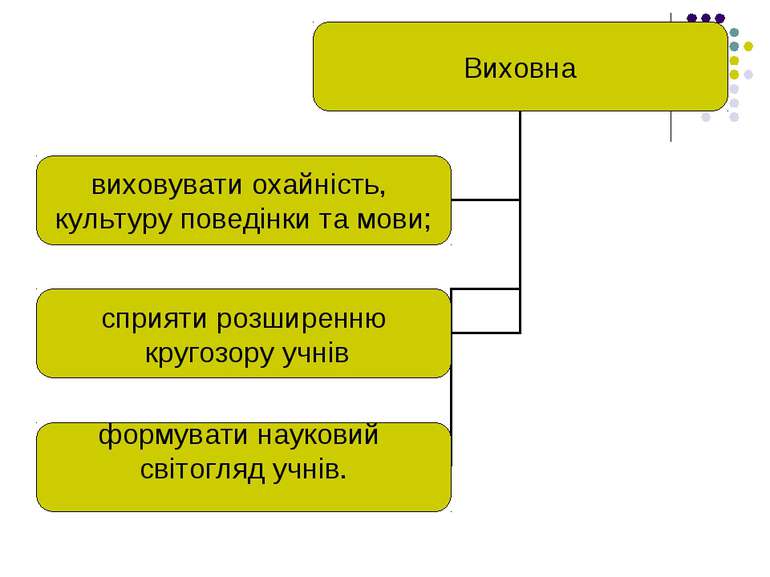
Завдання уроку: Розвивати дослідницьку та пізнавальну діяльність учнів. Показати практичне застосування гармонічних коливань. Показати взаємозв’язок між основними поняттями фізики та алгебри. Розвивати комунікативні здібності учнів. Гармонічні коливання вивчаються в курсі алгебри та фізики. Таким чином, ми будуємо місток: вивчаючи поняття в одному курсі, складаємо базу для іншого курсу. Повторюючи потім ці поняття в курсі алгебри та фізики, ми закріпимо його на практичному рівні.

Структура уроку: Організаційний момент 2 хв Постановка цілей уроку. Мотивація навчальної діяльності. 5 хв Вивчення нового матеріалу. 35 хв Закріплення матеріалу. 30 хв Підсумок уроку. 10 хв Домашнє завдання. 5 хв

Постановка цілей уроку. Мотивація навчальної діяльності. Фізик: Відомий італійський вчений Галілей говорив: «Філософія написана в тій величній книзі, яка завжди відкрита в нас перед очима (я маю на увазі Всесвіт), але яку неможливо зрозуміти, якщо заздалегідь не вивчити її мову». Математик: Її мова – це мова математики. Математика здавна має репутацію найточнішої галузі знань і є надійним знаряддям розкриття таємниць природи

Постановка проблемного питання: Математик: Приємно розпочати урок з такого прекрасного музичного супроводу. Та, сподіваюсь, присутні в цьому факті вбачають й іншу сторону. Фізик: А ось ми в них зараз і запитаємо. Як ви думаєте, що пов’язує музику з темою нашого уроку? Звучання струни, рух маятника, морські припливи, найрізноманітніші біоритми живих організмів – все це лише окремі приклади у нескінченній множині коливних або періодичних явищ.

Математик: А щоб описати їх, поставити на службу, людям треба побудувати математичні моделі таких явищ. Математичний опис періодичних процесів створювали вже вчені стародавнього світу. Так, вавилонські астрономи деякі закономірності руху Місяця і Сонця виразили у вигляді спеціальних таблиць, які вони назвали функціями. Теорія тригонометричних функцій, яку ми вивчали, теж є однією з найдавніших моделей періодичних явищ.

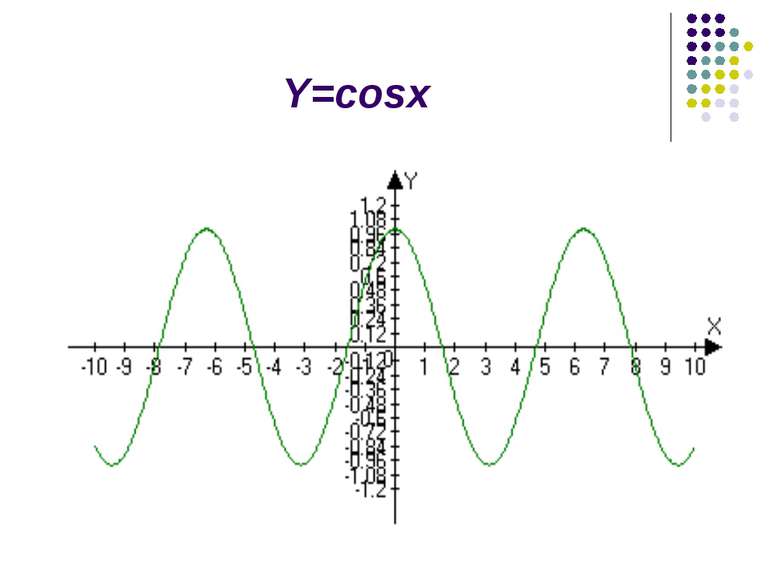
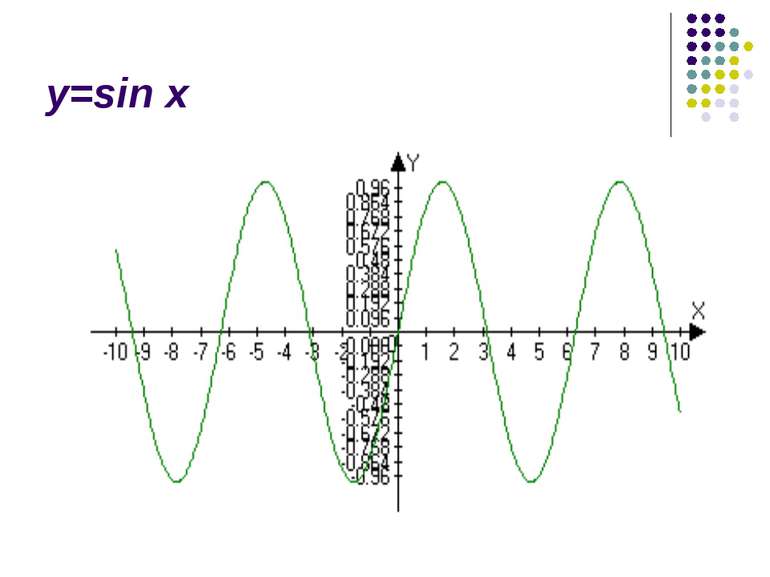
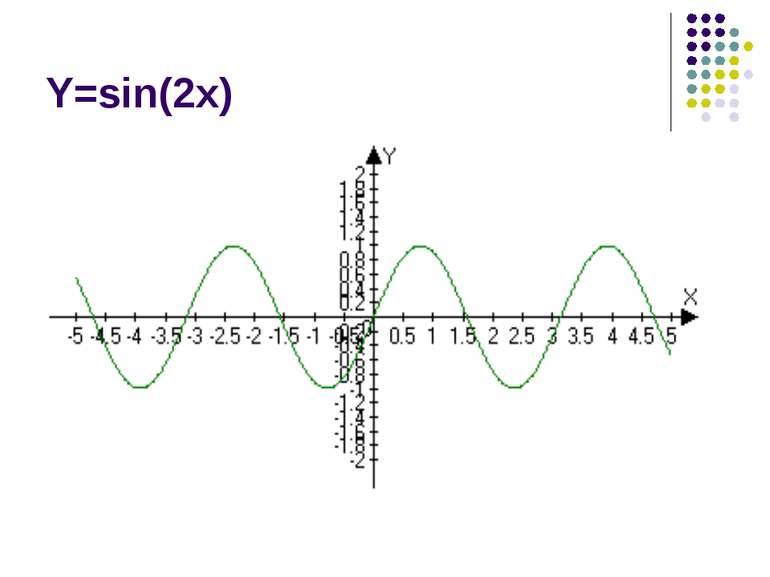
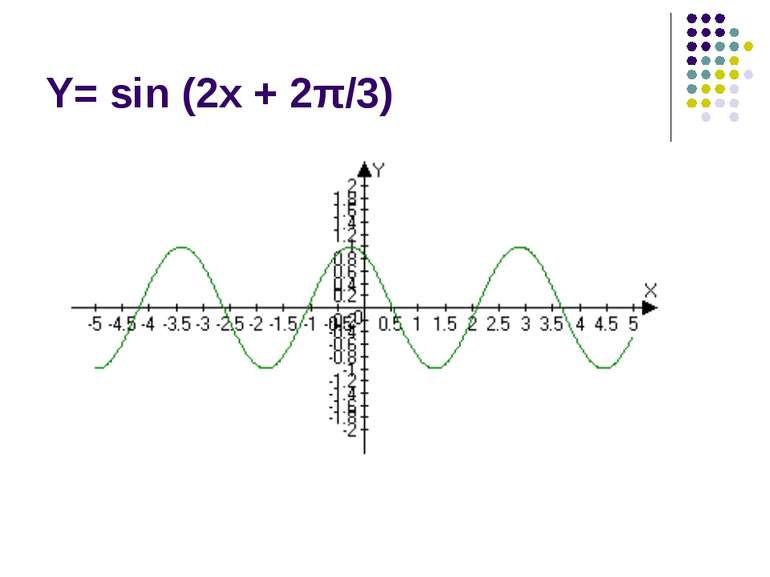
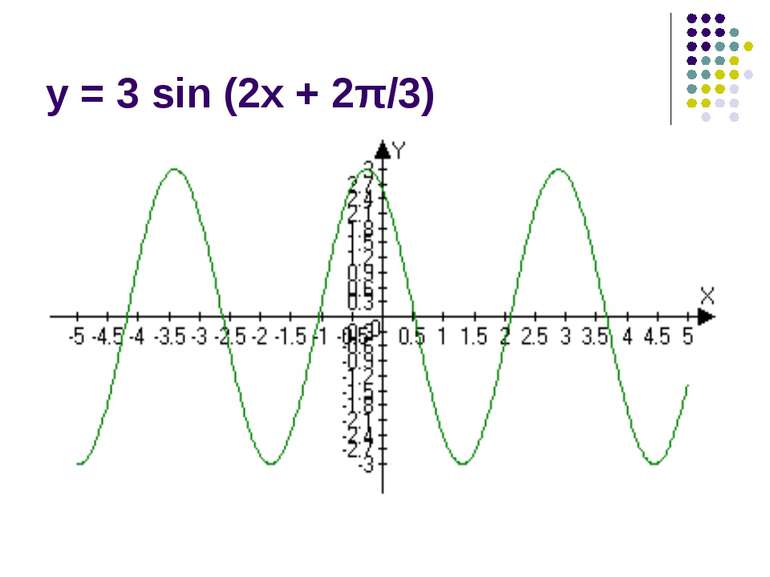
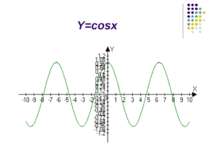
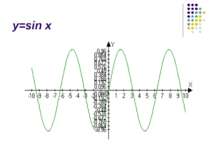
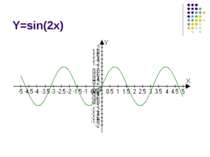
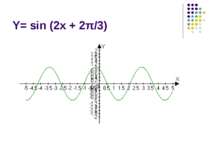
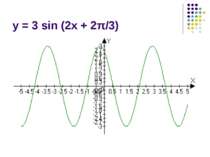
Вивчення нового матеріалу Сьогодні на уроці ми продовжимо вивчення тригонометричних функцій. Мета нашого уроку – розглянути приклади коливальних рухів, описати їх за допомогою математичних законів; навчитися будувати графіки тригонометричних функцій.

Y=cosx

y=sin x

Y=sin(2x)

Y= sin (2x + 2π/3)

y = 3 sin (2x + 2π/3)

Чим відрізняються дані графіки?

Закріплення нового матеріалу Фізик: Людина зустрічається з коливаннями і використовує їх у різних сферах своєї діяльності. У яких саме? Математик: Та чи завжди коливання є корисними? Фізик: Вібрації. Математик: Зрозуміло, що вібраційна хвороба – це дуже серйозне захворювання .Люди яких професій можуть захворіти нею?

Підсумок уроку Фізик: Завершуємо урок. Хочеться підкреслити, що коливання не є одним із типів руху в ряді інших, а являють собою фундаментальне явище, елемент того таємничого «алфавіту», за допомогою якого природа створює все, що нас оточує. Математик: Отже, друзі, чи згодні ви з тим, що глибокому дослідженню фізичних процесів допомагає математика? Тож що потрібно для того, щоб дослідити фізичне явище? А які моделі і методи ми використовували сьогодні?

Фізик: На сьогоднішньому уроці ми ще раз переконалися в тому, що математичні теорії є надійним знаряддям у розкритті таємниць природи. А коливання, про які ми говорили сьогодні, якщо будуть контролюватись людиною, будуть приносити велику користь. Але вони можуть перетворитися і на заклятого ворога. Тому треба вивчати коливання, знати їх властивості. І тут без математичних розрахунків точно не обійтись. Математик: А я не втримаюсь, щоб не процитувати слова індійського математика Бхаскара ІІ (ХІІ ст.): «Я глибоко шаную математику, бо ті, хто знайомі з нею, вбачають у ній засіб до розуміння всього існуючого».

Домашнє завдання: Творча робота. Уявіть собі, що ви сьогодні запросили на міжнародний симпозіум з дослідження коливальних процесів . З якого питання ви змогли б виступити, напишіть короткий зміст свого виступу на цьому симпозіумі.