Презентація на тему:
Опрацювання результатів

Л4 ОПРАЦЮВАННЯ РЕЗУЛЬТАТІВ ВИМІРЮВАНЬ

1. Опрацювання результатів прямих вимірювань 1.1 Загальні проблеми 1.2 Нехтування похибками 1.3 Заокруглення похибок 2. Опрацювання результатів непрямих (опосередкованих) вимірювань 3. Систематичні похибки в непрямих вимірах

1. Опрацювання результатів прямих вимірювань 1.1 Загальні проблеми

ОПРАЦЮВАННЯ РЕЗУЛЬТАТІВ ПРЯМИХ ВИМІРЮВАНЬ НЕПРЯМИХ (ОПОСЕРЕДКОВАНИХ) ВИМІРЮВАНЬ

Результати вимірювання - опрацьовані результати спостережень, що отримані в процесі вимірювальних експериментів

Опрацьовуючи результати, розв'язують дві задачі: першу - знаходять найкращу для вибраних методики і вимірювальних засобів, умов вимірювань та отриманих експериментальних даних оцінку значення вимірюваної величини

Опрацьовуючи результати, розв'язують дві задачі: другу - оцінюють характеристики точності вимірювання у вигляді характеристик похибки чи невизначеності (непевності) результату вимірювання.

Результат вимірювання є повноцінним за умови, що він супроводжується оцінкою його точності. Часто також повинен включати інші важливі дані, що забезпечує можливість порівняння результатів вимірювань, виконаних за однаковими чи різними методиками, різними засобами, в різних установах.

Данні, що можуть входити до показників точності імовірнісні показники кількість спостережень, їх статистичний розподіл, алгоритм опрацювання, характеристики вимірювальних засобів, умови вимірювань, способи корекції систематичних ефектів (похибок), тощо

Обсяг опрацювання результатів спостереженнь залежить від різновиду вимірювання, кількості експериментальних даних, вимог щодо точності вимірювання, апріорної інформації про систематичні та випадкові ефекти (похибки) вимірювання тощо.

Основні операції опрацювання первинних результатів вимірювань: - попередній аналіз результатів спостережень, їх систематизація, відкидання явно недостовірних; - виявлення та коригування систематичних ефектів (вивчення умов вимірювань, розрахунок і внесення поправок), часто методика вимірювання реалізує той чи інший спосіб коригування, що слід врахувати в алгоритмі опрацювання;

Основні операції опрацювання первинних результатів вимірювань: - виконання розрахунків згідно з вибраним алгоритмом; - аналіз випадкових ефектів, перевірка гіпотез про їх розподіл, вибір найефективніших оцінок шуканих величин; - оцінювання похибок від впливу завад; - оцінювання характеристик похибок числового алгоритму, його стійкості;

Основні операції опрацювання первинних результатів вимірювань: - підсумовування складових похибок результатів; - аналіз отриманих результатів; - подання результатів вимірювань та характеристик їх точності за відповідною формою.

Нехтування похибками

1. Опрацювання результатів прямих вимірювань 1.2 Нехтування похибками

При наявності кількох складових сумарної похибки виникає питання чи всі похибки треба враховувати. Можна встановити умову рн - Δ2 / Δ 1 нехтування малою похибкою Δ 2 порівняно з більшою Δ1, за якої сумарна похибка наближено дорівнює більшій Очевидно, що для різних характерів похибок і різних вимірювань ця умова буде різною.

Нехтування систематичними похибками Умова нехтування приймає вигляд

У метрологічній практиці прийнято при лабораторних вимірюваннях для науково-технічних досліджень непевність оцінювання похибки рн може досягати 10 %...15 % (рн=1/10...~1/7) від її значення. При високоточних вимірюваннях (наприклад, при дослідженні еталонів) допустиму непевність оцінки похибки зменшують до 5 % (рн=1/20) і навіть менше, при технічних вимірюваннях - вона може досягати 20 % (рн =1/5).

При наявності більшої кількості похибок

Нехтування випадковими похибками Оцінюючи сумарний вплив випадкових похибок використовують їх їх дисперсії D1 = σ2Δ1, D2 = σ2Δ2

Умова нехтування випадковою похибкою де r12 - коефіцієнт кореляції між цими похибками

Для повністю корельованих похибок (r12=1) ця умова стає такою, як для систематичних похибок Р ≤ РН

Для некорельованих випадкових похибок (r12=0) ця умова спрощується

Некорельованою випадковою похибкою можна знехтувати за умови, якщо її стандартне відхилення не перевищує р ≈ 1/(3,5 -5- 4) іншої - під час високоточних метрологічних вимірювань; р ≈ 1/2,5 іншої - під час науково-дослідних (лабораторних) вимірювань; р ≈ І/2 іншої - під час технічних вимірювань.

За відсутності інформації про коефіцієнт кореляції можна взяти його середньоквадратичне значення р ≈ 1/12 - під час високоточних метрологічних вимірювань; р ≈ 1/(5 - 7) - під час науково-дослідних (лабораторних) вимірювань; р ≈ 1/3,3 - під час технічних вимірювань.

Заокруглення похибок Похибку заокруглення можна розглядати як окрему складову похибки, якою нехтують. Тому спосіб заокруглення похибок безпосередньо випливає з умови нехтування малою похибкою: - похибка заокруглення похибки не може перевищувати значення, отримувані з умови нехтування.

1. Опрацювання результатів прямих вимірювань 1.3 Заокруглення похибок

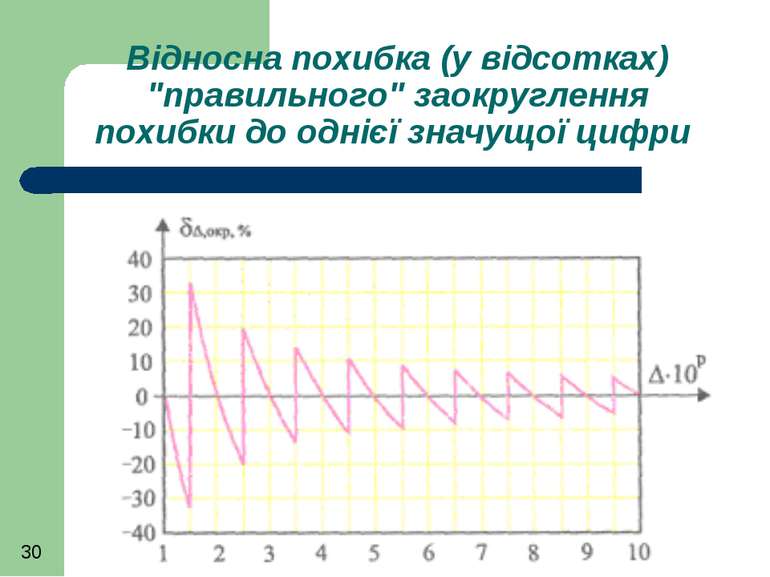
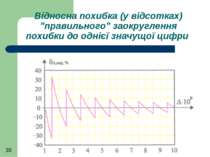
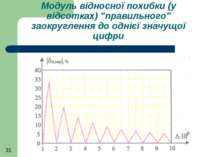
Якщо заокруглювати похибку до однієї значущої цифри, то абсолютна похибка заокруглення справжнього значення похибки не перевищить половини десяткового розряду.

Відносна похибка заокруглення при зміні справжнього (незаокругленого) значення похибки від 1 до 9,999 одиниць цього розряду набуде значення де р - вага розряду похибки

Відносна похибка (у відсотках) "правильного" заокруглення похибки до однієї значущої цифри

Модуль відносної похибки (у відсотках) "правильного" заокруглення до однієї значущої цифри

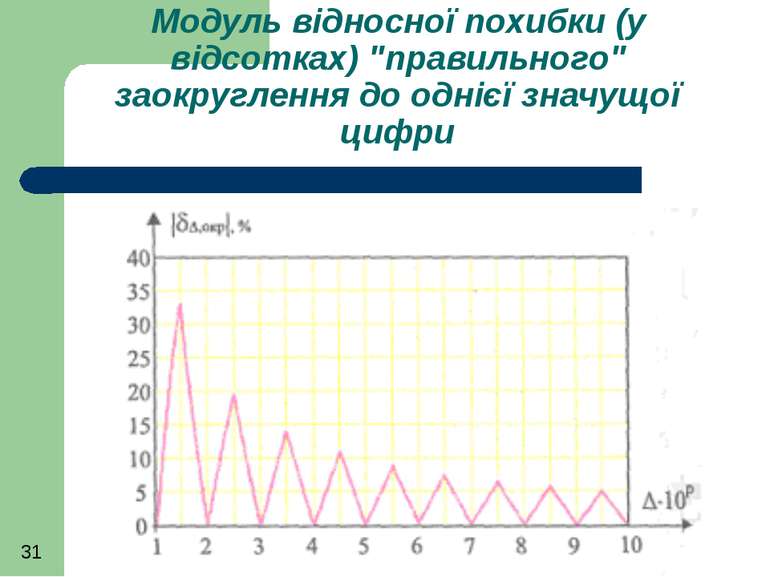
При технічних вимірюваннях умовою нехтування похибкою заокруглення похибки є відношення похибки заокруглення похибки до її точного значення на рівні понад 1/5 (до 20 %). Для виконання цієї умови необхідно заокруглювати до двох значущих цифр похибки, перша значуща цифра яких починається з 1

Для таких значень похибок максимальна похибка заокруглення в околі Δ=1,05 і вона становить параметр нехтування РН=1/21

Решту похибок (перша значуща цифра яких 2,3,..., 9) заокруглюють до однієї значущої цифри). Найбільшу похибку отримуємо в околі Δ=2,5 і вона становить параметр нехтування становить РН=1/5.

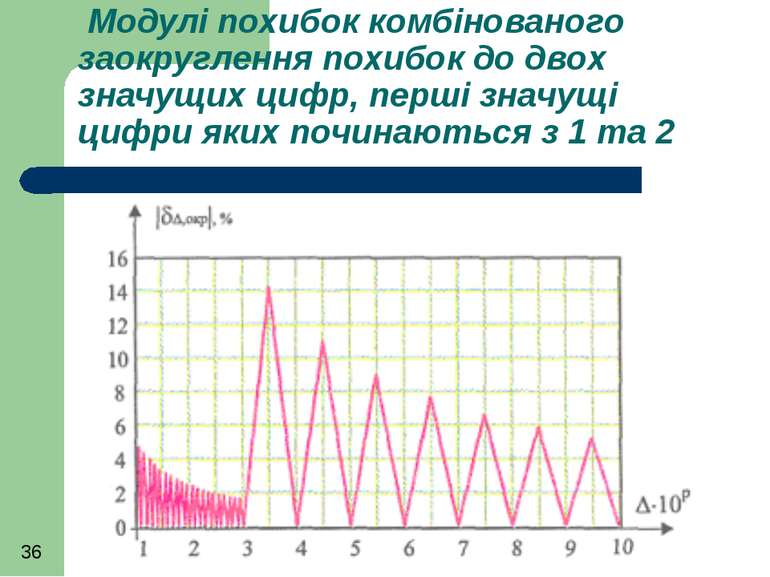
На практиці рекомендують заокруглювати до двох значущих цифр також похибки, першою значущою цифрою яких є 2

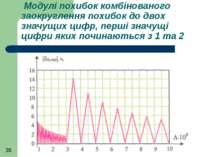
Модулі похибок комбінованого заокруглення похибок до двох значущих цифр, перші значущі цифри яких починаються з 1 та 2

Загалом у технічних вимірюваннях результати вимірювань подаються без оцінок їх точності. Ця точність закладена у відповідних засобах та методах вимірювань. Граничні чи інші характеристики похибок тут є наперед відомими, тому що вимірювальні засоби та вимірювальна схема підібрані у такий спосіб, щоб одержувати результати вимірювань заданої точності (встановленої ще на етапі планування таких вимірювань).

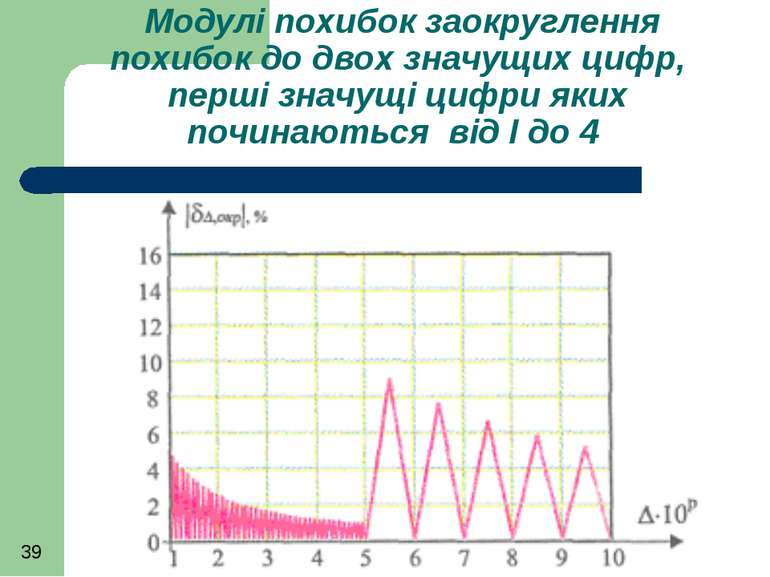
При виконанні наукових (лабораторних) вимірюваннь похибки, перші значущі цифри яких є 1, 2, 3 і 4, необхідно заокруглювати до двох значущих цифр.

Модулі похибок заокруглення похибок до двох значущих цифр, перші значущі цифри яких починаються від І до 4

Результат вимірювання і довірчі границі випадкової похибки За нехтовно малих систематичних похибок, оцінивши довірчі границі Δв дов випадкової похибки, результат вимірювання записують із зазначенням довірчої ймовірності Рдов, кількості опрацьовуваних результатів спостережень n і рекомендованої густини (чи апроксимації густини) розподілу Y = (y ± Δв дов ); Рдов, n ; вип.пох.: розподіл

Наприклад R = (53,65 ± 0,45) Ом; Рдов = 0.95, = 17; вип. пох.: розп. норм

Сумісне підсумовування систематичних та випадкових похибок Оцінка систематичної похибки вимірювання (або її нескоригованого залишку) може мати форму безумовних Δс,гр, або довірчих Δс дов. границь Випадкову складову зазвичай характеризують довірчими границями Δс дов.

Довірчі границі сумарної похибки Якщо довірчі ймовірності систематичної та випадкової похибок різні, то необхідно перерахувати відповідні границі або у разі неможливості - прийняти меншу довірчу імовірність.

2. Опрацювання результатів непрямих (опосередкованих) вимірювань

При непрямих (опосередкованих) вимірах виміряється не сама величина безпосередньо, а інші величини, зв'язані певною залежністю з величиною, що підлягає виміру, похибка результату залежить від похибки кожного з результатів вимірів, що входять у непрямий вимір.

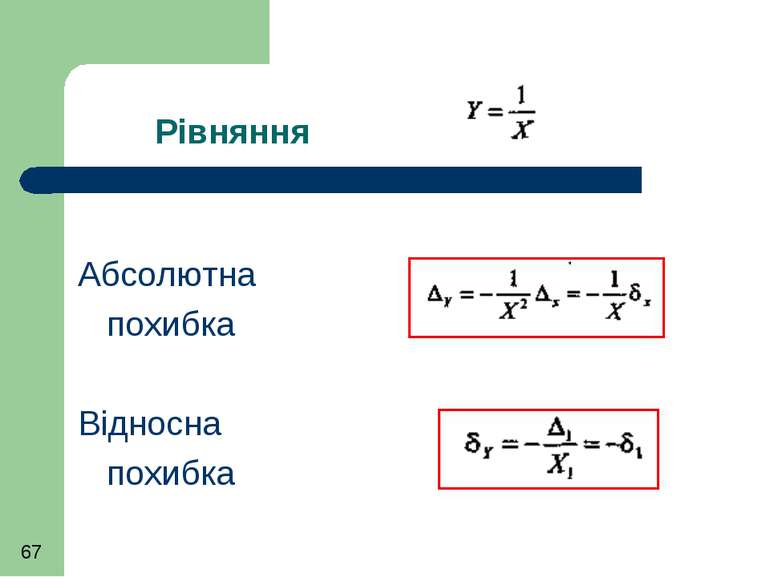
При непрямих (опосередкованих) вимірах Значення величини Y знаходять за результатами безпосередніх вимірювань величин Х1, Х2, Х3,…, ХN Y = f (X1, X2, X3,…, XN)

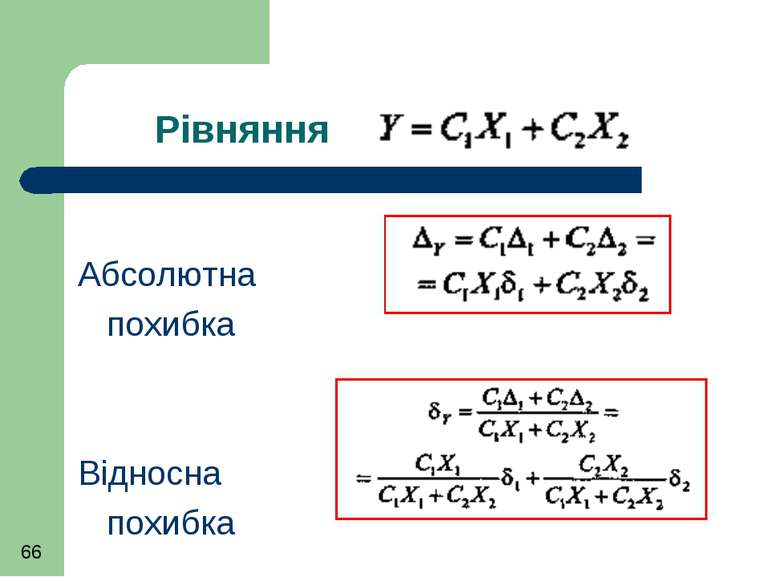
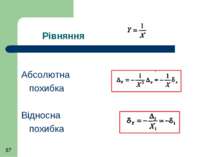
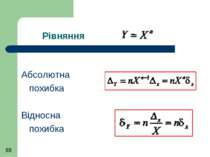
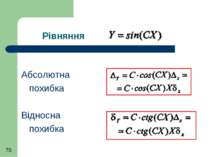
Рівняння результату виміру має вигляд причому кожна з величин має систематичну похибку Δсі.

З урахуванням наявності систематичних похибок непрямих вимірів похибка результату Δс(y) = f (x1 + Δс1; x2 + Δс2;…xm+Δсm) – - f (x1,x2,…xm) Це рівняння не дозволяє визначити внесок кожної похибки прямого виміру в сумарну похибку непрямого виміру.

Для визначення похибки непрямого виміру використають розкладання в ряд Тейлора рівняння вимірювання в околі результатів вимірювання аргументів.

За умови, що похибки малі вираз для похибки приймає вид де сі = ∂f/∂xi – часткова похідна функція по і-тому аргументу (коефіцієнт впливу ), обчислена при аргументах, що дорівнюють їх результатам вимірювань

При лінійній залежності ця формула справедлива для будь-яких значень похибки. Виходячи з неї можуть бути виведені вирази для випадків, що найбільше часто зустрічаються.

Похибка опосередкованого вимірювання оцінюється в такій послідовності: Визначається вираз похибки. Оцінюються характеристики окремих складових похибок вимірювань величин-аргументів. При необхідності коригуються їх систематичні похибки. Оцінюють характеристики сумарної похибки. Записують результат вимірювання із вказанням його непевності (невизначеності)

Вирази похибки опосередкованого вимірювання залежать від виду рівняння вимірювання (функції) і часто в одних випадках вираз абсолютної похибки є значно простішим, ніж відносної, а в інших - навпаки.

Загальні рекомендації - якщо рівняння вимірювання містить добутки, частку, піднесення до степеня, добування коренів, то доцільніше оперувати відносною похибкою; - якщо рівняння вимірювання є алгебраїчною сумою чи містить інші, ніж перераховані вище, нелінійні функції, то доцільно оперувати абсолютною похибкою.

3.СИСТЕМАТИЧНІ ПОХИБКИ В НЕПРЯМИХ ВИМІРАХ

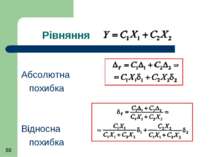
Систематична похибка суми величин Рівняння непрямого виміру має вигляд y = x1 + x2 вираз для визначення сумарної абсолютної похибки Δ с(y) = Δс1 + Δс2

Систематична похибка суми величин Для більш загального випадку Рівняння вимірювання Абсолютна сумарна похибка

Систематична абсолютна похибка суми величин дорівнює сумі абсолютних похибок складових

Систематична похибка суми величин Враховуючи, що Δ с(y) = Δс1 + Δс2= x1δ1 + x2δ2 Вираз для відносної похибки

Систематична похибка різниці величин Рівняння непрямого виміру y = x1 - x2 Абсолютна похибка різниці Δ с(y) = Δс1 - Δс2 Відносна похибка різниці

При визначенні сумарної похибки необхідно враховувати знаки систематичних похибок

Систематична похибка добутку величин Рівняння непрямого виміру y = x1 • x2 Абсолютна систематична похибка добутку Δс(y) = (x1 + Δc1)(x2 + Δc2) – x1x2 = x1 Δc2 + x2 Δc1 + Δc1 Δc2

Систематична похибка добутку величин Відносна похибка результату добутку непрямого виміру

Систематична похибка добутку величин Якщо похибки малі, то можна зневажити добутком похибок, як величиною другого порядку малості і отримати вирази для похибок абсолютної відносної

Систематична відносна похибка добутку дорівнює сумі відносних похибок аргументів.

Рівняння Абсолютна похибка Відносна похибка

Рівняння Абсолютна похибка Відносна похибка

Рівняння Абсолютна похибка Відносна похибка

Рівняння Абсолютна похибка Відносна похибка

Рівняння Абсолютна похибка Відносна похибка

Урахування випадкових похибок Для визначення впливу на результат вимірювання випадкових похибок можуть бути отримані подібні формули на базі середніх значень (математичного очікування) вимірювальної величини та їх середньоквадратичних відхилень.