Презентація на тему:
Визначні математики світу

Презентацію підготувала Дригант В.М., учитель математики Монастирищенського НВК «Ліцей – ЗОШ І-ІІІ ступенів «Ерудит»

Евклід Архімед (ARCHIMEDES) Паскаль Рене Декарт Ньютон П'єр де Ферма Лейбніц  Піфагор Ейлер Галуа М.І.Лобачевський Колмогоров Ковалевська Ґаус Фалес З М І С Т

Названі на честь Евкліда Любомудріє Начала Біографічна довідка, ілюстрації до змісту

«Начала» Основний твір Евкліда називається «Начала». Книги з такою ж назвою, в яких послідовно викладалися всі основні факти геометрії і теоретичної арифметики, складалися раніше Гіппократом Хіосським, Леонтом і Февдієм. Проте «Начала» Евкліда витіснили всі ці твори з ужитку і протягом більш ніж двох тисячоліть залишалися базовим підручником геометрії. Створюючи свій підручник, Евклід включив в нього багато з того, що було створене його попередниками, обробивши цей матеріал і звівши його воєдино. «Начала» складаються з тринадцяти книг. Перша і деякі інші книги передують списком визначень. Першій книзі передує також список постулатів і аксіом. Як правило, постулати задають базові побудови (наприклад, «потрібно, щоб через будь-які дві точки можна було провести пряму»), а аксіоми — загальні правила виведення при операції з величинами (наприклад, «якщо дві величини дорівнють третій, вони рівні між собою»). З сучасної точки зору, різниці між постулатами і аксіомами нема. У I книзі вивчаються властивості трикутників і паралелограмів; цю книгу вінчає знаменита теорема Піфагора для прямокутних трикутників. Книга II, виходить від піфагорійців, присвячена так званій «геометричній алгебрі». У III і IV книгах висловлюється геометрія кіл, а також вписаних і описаних багатокутників; при роботі над цими книгами Евклід міг скористатися творами Гіппократа Хіосського. У V книзі вводиться загальна теорія пропорцій, побудована Евдоксом Кнідським, а в VI книзі вона додається до теорії подібних фігур. VII—IX книги присвячені теорії чисел і знов посилаються до піфагорійців; автором VIII книги, можливо, був Архіт Тарентський. У цих книгах розглядаються теореми про пропорції і геометричні прогресії, вводиться метод для знаходження найбільшого загального дільника двох чисел (відомий нині як алгоритм Евкліда), будується парні довершені числа, доводиться нескінченність множини простих чисел. У X книзі, що є найоб'ємнішою і найскладнішою частиною «Начал», будується класифікація іррациональностей; можливо, що її автором є Теєтет Афінський. XI книга містить основи стереометрії. У XII книзі за допомогою методу вичерпання доводяться теореми про співвідношення площ кіл, а також об'ємів пірамід і конусів; автором цієї книги за загальним визнанням є Евдокс Кнідський. Нарешті, XIII книгу присвячено побудові п'яти правильних багатогранників; вважається, що частина побудов була розроблена Теєтетом Афінським. У рукописах, що дійшли до нас, до цих тринадцяти книг додані ще дві. XIV книга належить александрійцу Гипсиклу (біля 200 р. до н. е.), а XV книгу створено під час життя Ісідора Мілетського, будівельника храму св. Софії в Константинополі (початок VI ст. н. е.). «Начала» надають загальну основу для подальших геометричних трактатів Архімеда, Аполлонія і інших античних авторів; доведені в них припущення вважаються загальновідомими. Коментарі до «Начал» в античності складали Герон, Порфирій, Папп, Прокл, Симплікій. Зберігся коментар Прокла до I книги, а також коментар Паппа до X книги (у арабському перекладі). Від античних авторів коментаторська традиція переходить до арабів, а потім і до Середньовічної Європи. У створенні і розвитку науки Нового часу «Начала» також зіграли важливу ідейну роль. Вони залишалися зразком математичного трактату, що строго і систематично висловлює основні положення тієї або іншої математичної науки.

Названі на честь Евкліда Евклідова геометрія Евклідова відстань Евклідова норма Евклідове кільце Евклідів простір Алгоритм Евкліда

Любомудріє Что и требовалось доказать. Нет царского пути к геометрии. Если теорему так и не смогли доказать, она становится аксиомой. То, что принято без доказательств, может быть отвергнуто без доказательств. При некоторых необычных и весьма таинственных обстоятельствах отдельные четные числа ведут себя как нечетные. Для тирана и для могущественного города, господствующего над другими городами, все, что выгодно, то и разумно. Как-то раз древнегреческого геометра Евклида спросили: - Что бы ты предпочел - два целых яблока или четыре половинки? - Конечно, четыре половинки. - А почему? Это ведь одно и то же. - Отнюдь. Выбирая два целых яблока, как я узнаю, червивые они или нет? Фрагмент старого папіруса з діаграмами з "Элементи геометрії" Евкліда Papyrus found among the remarkable rubbish piles of Oxyrhynchus in 1896-97 by the renowned expedition of B. P. Grenfell and A. S. Hunt. It is now located at the University Pennsylvania

Евклі д (грец. Ευκλείδης; близько 365 — близько 300 до н. е.) — старогрецький математик і визнаний основоположник математики. Родом з Афін, був учнем Платона. Автор найдавніших трактатів з математики, що дійшли до сьогодення.

АРХІМЕД (ARCHIMEDES) Любомудріє Біографія Найпопулярніший винахід Архімеда Наукова спадщина Легенди, пов'язані із життям Архімеда Задумливий Архімед, Доменіко Фетті до змісту

Золота корона Відома оповідь про те, як Архімед зумів визначити, чи зроблена корона сіракузького тирана Гієрона II з чистого золота або ж ювелір підмішав значну кількість срібла. Питома вага золота на той час вже була відомою, але складність полягала в тому, щоб точно визначити об'єм корони, адже вона мала неправильну форму. Архімед довгий час розмірковував над цим завданням. Зрештою, коли він приймав ванну, йому в голову прийшла блискуча ідея: занурюючи корону у воду, можна визначити її об'єм, вимірявши об'єм витісненої нею води. Згідно з легендою, Архімед вискочив голий на вулицю з криком «Еврика!» (дав.-гр. εὕρηκα!), що означало буквально «Знайшов!». Так науковець відкрив основний закон гідростатики, нині відомий як закон Архімеда. Корабель «Сіракосія» Інша легенда розповідає, що побудований Гієроном в подарунок єгипетському цареві Птолемею III важкий багатопалубний корабель «Сіракосія», який жодним чином не вдавалося спустити на воду. Архімед спорудив систему блоків (фактично поліспаст), за допомогою якого він зміг виконати цю роботу одним рухом руки. За легендою, Архімед заявив при цьому: «Будь в моєму розпорядженні інша Земля, на яку можна було б встати, я зсунув з місця нашу» (дав.-гр. δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω). В іншому варіанті, дещо більш поширеному, його репліка передається так: Дайте мені точку опори, і я поверну Землю! Облога Сіракуз нженерний геній Архімеда з особливою силою проявився під час облоги Сіракуз римлянами в 212 року до н. е. в ході Другої Пунічної війни, коли йому в цей час виповнилося вже 75 років. Побудовані Архімедом потужні метальні машини закидали римські війська важкими каменями. Думаючи, що вони будуть в безпеці біля самих стін міста, римляни кинулися туди, але в цей час легкі метальні машини близької дії закидали їх градом ядер. Потужні крани захоплювали залізними гаками кораблі, піднімали їх догори, а потім кидали вниз, так що кораблі переверталися й тонули[10]. Римляни змушені були відмовитися від задуму взяти місто штурмом і перейшли до облоги. Знаменитий історик давнини Полібій писав:«Така чудова сила однієї людини, одного дарування, вміло спрямована на будь-яку справу… римляни могли б швидко оволодіти містом, якби хто-небудь вилучив з середовища сіракузян одного старця».Навіть під час облоги Архімед не давав спокою римлянам: римський флот спалили захисники міста за допомогою дзеркал і відполірованих до блиску щитів, сфокусованих на сонячні промені за наказом Архімеда. Цю легенду двічі спростовували у телепередачі «Руйнівники легенд» (у 3 сезоні, епізод 46, та 2 сезоні, епізод 16). Існує думка, що кораблі підпалювалися влучно кинутими запаленими снарядами, а сфокусовані промені служили лише прицільною міткою для баліст. Однак експеримент грецького вченого Іоанніса Саккаса (1973) показав інше. Він використовував 70 мідних дзеркал і з їх допомогою успішно підпалив фанерну модель римського корабля з відстані 50 м. Тільки внаслідок зради римлянам вдалось взяти Сіракузи восени 212 року до н. е. Архімед

Архімед (дав.-гр. ᾽Αρχιμήδης; близько 287 до н. е., Сіракузи — 212 до н. е., Сіракузи) — давньогрецький математик, фізик, інженер, винахідник та астроном. Хоча дуже мало деталей відомо про його життя, він вважається одним з найвидатніших науковців античності. Серед його досягнень у фізиці, — заснування гідростатики, статики та пояснення принципу важеля. Йому приписують винайдення новаторських механізмів, включно з облоговими машинами та гвинтовим насосом, що названий на його честь. Сучасними експериментами перевіряли твердження, що Архімедові машини могли піднімати кораблі в повітря та підпалювати їх за допомогою набору дзеркал.[1] Архімед, як правило, вважається найвидатнішим математиком античності та одним з найвидатніших всіх часів.[2][3] Він використовував метод вичерпування, щоб розрахувати площу обмежену дугою параболи шляхом розрахунку суми нескінченного ряду і дав надзвичайно точне наближення числа пі. Він також винайшов спіраль, що носить його ім’я, формули для розрахунку об’ємів поверхонь обертання та оригінальну систему для вираження дуже великих чисел. Архімед помер під час облоги Сіракуз, вбитий римським солдатом, попри виданий наказ не заподіювати йому шкоди. Цицерон описує свій візит на могилу Архімеда, яку увінчувала сфера вписана в циліндр. Архімед довів, що сфера має дві треті від площі та об'єму описаного циліндра (включно з його основами) і вважав це одним з своїх найбільших математичних досягнень. В часи античності Архімед був більше відомий через свої винаходи, а не математичні роботи. Математики з Александрії читали та цитували його, проте перша повна компіляція була зроблена тільки 530 р. н.е. Ісидором з Мілету, тоді як коментарі праць Архімеда написані Євтокієм в шостому столітті н.е. вперше відкрили їх для широкої аудиторії. Ті кілька письмових копій Архімедових робіт, які вціліли протягом Середніх віків, були впливовими джерелами ідей для науковців в часи Ренесансу.[4] Завдяки віднайденому в 1906 році Палімпсесту Архімеда, де були раніше невідомі його роботи, вдалося пролити світло на те як він отримував математичні результати.[5]

Архімед Кохання — це теорема, яку кожного дня потрібно доводити Дайте мені точку опори і я переверну Землю Дайте мені, де стати, і я зрушу світ Існує безліч речей, які здаються загадковими для людей, які не вивчали математику Любомудріє

ІНШІ НАУКОВІ ДОСЯГНЕННЯ Особливо пишався Архімед знайденим співвідношенням між об’ємами вписаних одне в одного конуса, шара і циліндра — 1:2:3. Навіть у завіті шар, вписаний у циліндр, був вигравіруваний на надгробку могили Архімеда. Саме за цією ознакою Цицерону вдалося знайти його могилу через 150 років після смерті. Архімед вважав себе радше фізиком, якщо повернути цьому слову значення, яке надавали йому древні греки. У ті часи науки являли собою цілісне, пов’язане методом міркування, знання. У роботах Архімеда об’єм шара вичисляється з допомогою правила важеля, закон плавучості тіл з’являється при рішенні задачі про вичислення об’єму, безкінечність ряду натуральних чисел доводиться з допомогою підрахунку піщинок. Методи Архімеда пізніше буде використовувати Галілей, наприклад, при вичисленні квадратури параболи (вичислення площі під кривою), вирізаючи та зважуючи сектори, а також при виведенні закони рівноприскореного руху. Говорять про інженерний геній Архімеда, приводячи як приклад машини для оборони Сіракуз, які базувалися на принципі важеля, а також гвинт для підйому води. Звісно ж, гвинт та важіль були відомими ще задовго до Архімеда. А його ім’я вони носять тому, що він чітко сформулював принципи роботи і використав їх для рішення інших завдань. Принцип важеля стане в майбутньому основою для створення механіки, а метод ділення фігури на безкінчено тонкі полоски і складення їхніх об’ємів з обов’язковим доведенням того, що обмеження зверху і знизу зводяться до одного й того ж обмеження — основою для інтегрального числення. Фраза, яка приписується Архімеду: “Дайте мені точку опори і я переверну Землю” пов’язана саме з принципом важеля. Тим самим методом доведення користується Архімед в роботі “Про плавучість тіл”. Відоме кожному школяреві наближення числа “пі” як периметра правильних багатокутників зі збільшенням числа сторін також було відоме до Архімеда, але строго доведене саме ним. Архімед

Найпопулярніший винахід Архімеда гвинт, пристрій для підйому води відомий як гвинтовий насос Архімеда.Архимедів гвинт до сих пір використовується в зрошенні сільськогосподарських культур і очисних споруд. Архімед показує своїм учням, як насос використовується для підйому води . Архімед Напевно, навчався в Олександрії, Єгипет

Винайшов загальні методи обчислення площі криволінійних плоских фігур і об'ємів тіл, обмежених кривими поверхнями, і застосував ці методи до багатьох частинних випадків: до кола, сфери, довільного сегменту параболи тощо.. Дав метод обчислення числа Пі і встановив, що це число знаходиться між  Вчений обчислив відношення довжини кола до його діаметру (число π). Він розглядав правильні багатокутники вписані і описані навколо кола. Порівнюючи периметри багатокутників можна визначити верхню і нижню границі для ободу кола. Ця метода дозволяла визначити з довільною точністю число π, як відношення довжини кола до діаметра. Архімед зробив оцінку для числа π вибравши багатокутник з певною кількістю сторін. Запропонував також наближений метод обчислення квадратних коренів, сформулював основні положення гідростатики, створив низку машин і споруд.

Наукова спадщина Архімед Донині збереглись такі праці Архімеда: Квадратура параболи (τετραγωνισμὸς παραβολῆς) — визначається площа сегмента параболи. Про кулю і циліндр ( περὶ σφαίρας καὶ κυλίνδρου) — доводиться, що об'єм кулі дорівнює 23 від обсягу описаного навколо неї циліндра, а площа поверхні кулі дорівнює площі бічної поверхні цього циліндра. Про спіралі ( περὶ ἑλίκων) — виводяться властивості спіралі Архімеда. Про коноїди і сфероїди ( περὶ κωνοειδέων καὶ σφαιροειδέων) — визначаються обсяги сегментів параболоїда, гіперболоїда і еліпсоїдів обертання. Про рівновагу пласких фігур ( περὶ ἰσορροπιῶν) — виводиться закон рівноваги важеля; доводиться, що центр ваги плаского трикутника розташований в точці перетину його медіан; знаходяться центри інерції паралелограма, трапеції і параболічного сегмента. Послання до Ератосфена про метод ( πρὸς Ἐρατοσθένην ἔφοδος) — виявлено в 1906 у, з тематики частково дублює роботу «Про кулю і циліндр», але тут використовується механічний метод доведення математичних теорем. Про плаваючі тіла ( περὶ τῶν ὀχουμένων) — виводиться закон плавання тіл; розглядається задача про рівновагу перетину параболоїда, що моделює корабельний корпус. Вимірювання кола ( κύκλου μέτρησις) — до нас дійшов тільки уривок з цього твору. Саме в ньому Архімед обчислює наближення для числа π. Псамміт ( ψαμμίτης) — вводиться спосіб запису дуже великих чисел. Стомахіон ( στομάχιον) — подано опис популярної гри. Задача Архімеда про биків ( πρόβλημα βοικόν) — ставиться задача, яка приводиться до рівняння Пелля. Збереглися тільки в арабському перекладі такі праці Архімеда: Трактат про побудову близько кулі тілесної фігури з чотирнадцятьма основами; Книга лем; Книга про побудову кола, розділеного на сім рівних частин; Книга про дотичні кола.

РЕНЕ ДЕКАРТ (RENE DESCARTES) Біографічна довідка Любомудріє Відкриття Метафізика Декарта, 2007 автор:О.Войтович Декарт за роботою. до змісту

Рене Декарт (1596 - 1650) Рене Декарт відомий, як великий філософ, ніж математик. Але саме він був піонером сучасної математики, його досягнення в цій галузі настільки видатні, що він по праву входить до числа великих математиків. Рене Декарт з королевою Христиною Народився 31 березня 1596 Ла-е-ан-Турен Помер 11 лютого 1650 Стокгольм Місце проживання Париж Громадянство   Франція Галузь наукових інтересів математика, фізика, оптика,філософія

Любомудріє РЕНЕ ДЕКАРТ Бог може все, що я вважаю можливим Прагни перемагати швидше самого себе, ніж долю, і змінювати своє бажання, ніж порядок у світі. Здоровий глузд — найбільш розповсюджена річ у цьому світі, оскільки кожен думає, що він наділений ним повною мірою. Самотність потрібно шукати у великих містах. Найбільше заздрять славі. Неможливо вигадати чогось оригінального і малоймовірного, що не було б уже сказано кимось із філософів. Прагнення відмінностей при нестачі характеру згинає одну людину перед іншою. Ми можемо давати собі звіт щодо стану нашого здоров’я, але щодо стану розуму — ніколи. Люди, які займаються філософією частіше виявляються менш мудрими, ніж ті, хто ніколи нею не займався. Я мислю — отже існую. Правильно визначайте слова, і ви позбавите світ від половини непорозумінь. Всі науки настільки пов’язані між собою, що легше вивчати їх всі відразу, ніж якусь одну із них окремо від інших. Для того, щоб вдосконалити розум потрібно більше розмірковувати, ніж заучувати. Краще взагалі не прагнути відшукувати істини, ніж робити це без будь-якого методу. Мало мати хороший розум, головне — правильно його використовувати. Розпач — це страх без надії. Розум — це запалювальне скло, яке, воспламеняючи, саме залишається холодним.

ВЧЕННЯ Декарт прославив своє ім’я великою кількістю трактатів з математики та філософії. Основні з них: “Геометрія” (1637), “Міркування про метод…” (1637), “Начала філософії” (1644). Крім того він заклав основи аналітичної геометрії, дав поняття змінної величини і функції, ввів багато алгебраїчних визначень, висловив закон збереження руху, дав поняття імпульсу сили. Автор теорії, яка пояснює утворення небесних тіл вихоровим рухом частинок матерії (вихрі Декарта). Ввів поняття рефлексу (дуга Декарта). “Геометрія” (1637) “Міркування про метод…” (1637) “Начала філософії” (1644) IGDA/G. Dagli Orti РЕНЕ ДЕКАРТ

Видатний французький математик, один із основоположників аналітичної геометрії і теорії чисел, автор робіт в області теорії ймовірностей, оптики, численні нескінченно-малих величин.        У 1637 році він сформулював так звану Велику теорему Ферма.Теорема стверджує, що для будь-якого натурального n>2 i xyz0 рівняння не можна розв’язати в цілих (ірраціональних) числах. Формули інтегрування частинами Для невизначеного інтеграла: Для визначеного інтеграла: П'єр де Ферма Народився 17 серпня 1601 Бомон-де-Ломань,Франція Помер 12 січня 1665 Кастр, Франція Місце проживання Франція Національність француз Галузь наукових інтересів математика, фізика Відомий у зв'язку з: Аналітична геометрія Теорія ймовірностей Велика теорема Ферма Принцип Ферма

Блез Паскаль Бібліографічна довідка, ілюстрації Відкриття та винаходи Любомудріє Увічнення пам'яті до змісту

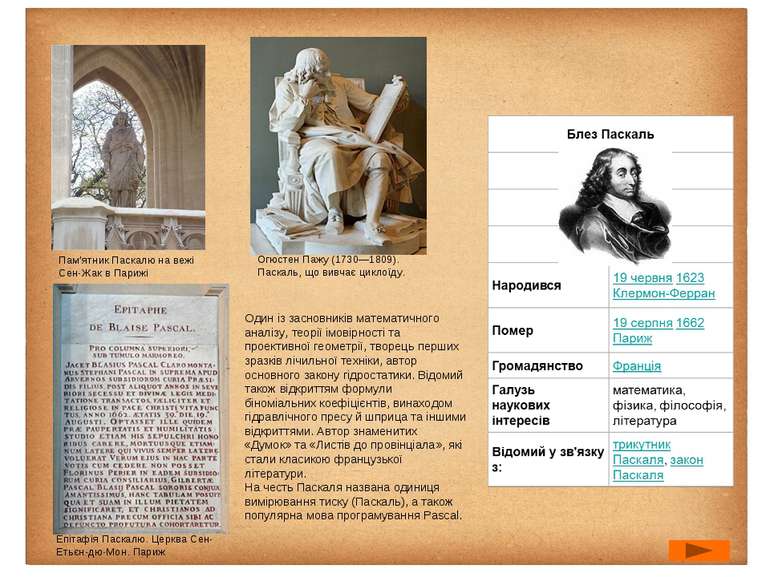
Огюстен Пажу (1730—1809). Паскаль, що вивчає циклоїду. Пам’ятник Паскалю на вежі Сен-Жак в Парижі Епітафія Паскалю. Церква Сен-Етьєн-дю-Мон. Париж Один із засновників математичного аналізу, теорії імовірності та проективної геометрії, творець перших зразків лічильної техніки, автор основного закону гідростатики. Відомий також відкриттям формули біноміальних коефіцієнтів, винаходом гідравлічного пресу й шприца та іншими відкриттями. Автор знаменитих «Думок» та «Листів до провінціала», які стали класикою французької літератури. На честь Паскаля названа одиниця вимірювання тиску (Паскаль), а також популярна мова програмування Pascal.

Блез Паскаль (1623-1662)     Видатний французький математик, фізик, літератор і філософ. Один із засновників математичного аналізу, теорії ймовірностей і проективної геометрії, автор основного закону гідростатики. П. Ферма і Б. Паскаль стали першотворцями теорії математичної  ймовірностей. Якось такий собі кавалер де Мере звернувся до Паскаля з приводу т. зв. "задачі про очки" у грі в карти та кістки. Паскаль тут же зав'язав листування з Ферма — і вони удвох за короткий термін встановили деякі основні положення теорії ймовірностей (1654). Звернення Паскаля до Ферма не було випадковим — на той час аналогічні задачі виникали у страховій справі, до якої як радник парламенту мав безпосереднє відношення П. Ферма. Ще в 1642 році Паскаль сконструював механічну обчислювальну машину для двох арифметичних дій. Принципи, які лягли в основу цієї машини, стали пізніше вихідними в конструюванні обчислювальних машин.

Відкриття та винаходи Гідравлічний прес Трикутник Паскаля Видатний французький математик, фізик, літератор і філософ. Один із засновників математичного аналізу, теорії ймовірностей і проективної геометрії, автор основного закону гідростатики. П. Ферма і Б. Паскаль стали першотворцями теорії математичної  ймовірностей. Якось такий собі кавалер де Мере звернувся до Паскаля з приводу т. зв. "задачі про очки" у грі в карти та кістки. Паскаль тут же зав'язав листування з Ферма — і вони удвох за короткий термін встановили деякі основні положення теорії ймовірностей (1654). Звернення Паскаля до Ферма не було випадковим — на той час аналогічні задачі виникали у страховій справі, до якої як радник парламенту мав безпосереднє відношення П. Ферма. Ще в 1642 році Паскаль сконструював механічну обчислювальну машину для двох арифметичних дій. Принципи, які лягли в основу цієї машини, стали пізніше вихідними в конструюванні обчислювальних машин. Равлик Паскаля - пласка Алгебраїчна крива 4-го порядку; подера окружності, конхоіда окружності щодо точки на колі, приватний випадок Декартова овала, вона також є епітрохоідой. Названа по імені Етьена Паскаля (батька Блеза Паскаля). Паскаліна, створена Блезом Паскалем у 1652 році. (лічильна машина: створив свою Паскаліну у віці 19 років, спостерігаючи за роботою свого батька, який працював збірником податків і був змушений часто виконувати довгі і обтяжливі розрахунк)

Увічнення пам'яті Паскаль кратер на Місяці ; одиниця вимірювання тиску системи СІ ; мова програмування Паскаль . Один з двох університетів у Клермон-Феррані . Щорічна французька наукова премія паскаліна

Любомудріє Паскаль Випадкові відкриття роблять тільки підготовлені розуми. Існує достатньо світла для тих, хто хоче бачити, і достатньо темряви для тих, хто не хоче. Чим розумніший, тим більше знаходиш оригінальних людей. Люди натовпу не здатні бачити відмінностей між людьми. Красномовство - це живопис думки . Світ - це сфера, центр якої всюди, а кола немає . Все наше достоїнство - в здатності мислити. Тільки думка підносить нас, а не простір і час , в яких ми - ніщо. Постараємося ж мислити гідно - в цьому основа моральності. Нехай людині немає ніякої вигоди брехати - це ще не означає, що вона буде говорити правду: брешуть просто в ім'я брехні. І сама блискуча мова набридає, якщо її затягнути Хочете, щоб про вас добре говорили, не говоріть про себе хорошого. Серце має докази, яких не знає розум Найбільше щастя , доступне людині, - любов - має служити джерелом всього піднесеного і шляхетного. У любові не буває віку, вона вічно молода

Ісаак Ньютон Любомудріє Біографічна довідка «яблуня Ньютона» до змісту

Ісаак Ньютон (1643-1727)     У галузі математики він завершив пошук і вдосконалення методів розв'язування знаменитих задач обчислення площ і об'ємів криволінійних фігур, проведення дотичних до кривих ліній у заданій точці. Вони охоплюють основи сучасного інтегрального і диференціального числення, або класичної вищої математики. Створення Ньютоном аналізу нескінченно малих відкрило нову епоху розвитку математики і всього математичного природознавства. Вклад Ньютона в математику не вичерпується створенням диференціального і інтегрального числення. Його праці зіграли також важливу роль в розвитку алгебри, аналітичної та проективної геометрії, вчення про числа. Нехай функція f неперервна на відрізку [а, b] та F — певна первісна для f на цьому відрізку, тоді: Народився 4 січня 1643  Англія, Вулсторп,Лінкольншир Помер 31 березня 1727  (84 роки)  Англія, Лондон, Кенінгстон Громадянство   Англія Проживання   Англія Ім'я при народженні Ісаак Ньютон Відомий Класична механіка Математичний аналіз Оптика

Любомудріє Ісаак Ньютон Геній є терпіння думки, зосередженої у відомому напрямку. Гіпотез не вигадую. Головна помилка виясняють Апокаліпсису полягала в тому, що вони на підставі Одкровення намагалися пророкувати часи і події, наче Бог зробив їх пророками. Завдяки цьому ці виясняють піддалися осуду самі і разом з тим порушили недовіру і до пророцтва взагалі. Але Божественне приречення полягало зовсім в іншому. Бог дав це Одкровення, так само як і Пророцтво Старого Завіту, не заради того, щоб задовольнити цікавість людей, роблячи їх здатними передбачати майбутнє, але заради того, щоб виконанням на ділі явив був світу святий Промисел Його, а не проникливість виясняють. Бо наступ подій, передбачених за кілька століть, служить переконливим доказом того, що всесвіт управляється Провидінням ... В останні ж часи величезний переворот, передбачений у Святому Письмі, відразу ж зверне погляди людей і на Пророцтво, і на грунтовне тлумачення їх. Якщо я бачив далі інших, то тому, що стояв на плечах гігантів. Мовою пророків весь Всесвіт, небо і земля позначають весь світ властей, що складається з престолів і народів, і всі речі в тому світі позначають відповідні речі в цьому. Пророцтво як провіщення майбутнього відноситься до стану Церкви в усі віки. Так як точний час народження і страждань Христових не суттєво для релігії, то на визначення його в перші століття християнства зверталося мало уваги. Ті, хто вперше почав святкувати ці події, приурочив їх до поворотним моментам року; так Благовіщення Святої Діви Марії було приурочено до дня весняного рівнодення; день Іоанна Хрестителя став святкуватися в день літнього сонцестояння; день святого Михаїла - на осіннє рівнодення і народження Христа - на зимове сонцестояння. Встановлення влади імператорів, царів і князів є встановлення людське. Влада соборів, синодів, єпископів і пресвітерів є встановлення людське. Учительство же пророків, включаючи в число їх Мойсея і апостолів, є встановлення божественне і корениться в глибокій істоті релігії; якщо Ангел з неба буде проповідувати інше Євангелію, ніж відкрили ці посланці Божий, «то анафема нехай буде». Я дивлюся на себе, як на дитину, яка, граючи на морському березі, знайшов кілька камінчиків погладжу і раковин попестрее, ніж вдавалося іншим, у той час як невимірний океан істини стелився перед моїм поглядом недослідженим.

Шанований пращур «Яблуня Ньютона». Кембрідж, Ботанічний сад Ісаак Барроу. Статуя в Трініті-коледжі.

Ґотфрід Вільгельм Лейбніц  (1646-1716 Любомудріє Біогафічна довідка Пам'ятні монети до змісту

Ґотфрід Вільгельм Лейбніц  (1646-1716) Видатний німецький філософ, логік, математик, фізик, мовознавець та дипломат. Передбачив принципи сучасної комбінаторики. Створив першу механічну лічильну машину, здатну виконувати додавання, віднімання, множення й ділення. Створив диференціальне й інтегральне числення і заклав основи двійкової системи числення. У рукописах і листуванні, які було надруковано лише в середині 19 ст., розробив основи теорії детермінантів. Мав надзвичайно широке коло наукових кореспондентів, багато з ідей викладено в рукописах і листуванні, що ще й досі повністю не надруковано. Лейбніц листувався майже з усіма тогочасними науковцями Європи, до його кореспондентів належало понад 600 осіб. Він переконав Фрідріха Вільгельма I заснувати Брандербурзьке наукове товариство (пізніше - Берлінська АН) і з 1700 був його президентом. На прохання Петра І  розробив проекти розвитку освіти і державного керування в Росії. Також доклав чимало зусиль для заснування наукових академій у Санкт-Петербурзі (яку було створено вже після його смерті) та Відні. Худ. Бернгард Крістоф Френк. Портрет Лейбніца Народився 1 липня (21 червня за старим стилем) 1646 Лейпциг, Саксонія Помер 14 листопада 1716 Гановер Національність Німець Галузь наукових інтересів математика, філософія Відомі учні Якоб Бернуллі

1646 - 1716

Любомудріє Ґотфрід Вільгельм Лейбніц Бібліотеки - це скарбниці всіх багатств людського духу. Горе - це занепокоєння душі, коли вона думає про втрачене благо, яким могла б довше насолоджуватися, або коли вона мучиться через випробуваного нею зараз зла. Якби геометрія так само суперечила нашим пристрастям і інтересам, як моральність, то ми б так само сперечалися проти неї і порушували її всупереч усім доказам. Заздрість є занепокоєння (незадоволення) душі, що випливає з того, що бажаним нам благом має інша людина, якого ми не вважаємо більш нас гідним володіти ним. Коли якась річ серед творінь Бога здається нам гідною осуду, ми повинні зробити висновок, що вона недостатньо нами зрозуміла і що мудрець, який спіткав би її, вирішив би, що неможливо навіть бажати чогось кращого. Любити - це знаходити в щасті іншого своє власне щастя. Любов є схильність знаходити задоволення в благо, досконало, щастя іншої людини. Музика є несвідома вправа душі в арифметиці. Теперішній час загрожує майбутнім. Цей світ - кращий зі світів. Наше щастя зовсім не перебуває і не повинно полягати в повному задоволенні, при якому не залишалося б більше нічого бажати, що сприяло б тільки отупіння нашого розуму. Вічне прагнення до нових насолод і новим досконалостям - це і є щастя. Скромні люди, будучи тільки свідками непристойного вчинку, відчувають відчуття, схожі на відчуття сорому. Я стою на тому, що погана голова, володіючи допоміжними перевагами і вправляючи їх, може перевершити саму кращу, подібно до того, як дитина може провести по лінійці лінію краще, ніж найбільший майстер від руки.

Леонард Ейлер (1707-1783) Біографічна довідка Наукові відкриття до змісту

Леонард Ейлер (1707-1783) Ейлер створив варіаційне числення, надав сучасну форму інтегральному численню, викладенню тригонометрії та арифметики, зробив вагомий внесок у дослідження теорії ймовірностей та її застосувань. Його праці виділили теорію диференціальних рівнянь в окрему дисципліну. Він був, по суті, засновником теоретичної фізики, механіки твердих тіл, гідродинаміки, гідравліки. Багато праць вчений присвятив геометрії, теорії чисел. Важко навіть перечислити всі галузі науки, в яких трудився учений. У середній школі логарифми та тригонометрію вивчають до цього часу "за Ейлером". Він також розширив множину визначення експоненційної функції на комплексні числа, і виявив звязок експоненти з тригонометричними функціями.Формула Ейлера стверджує, що для будь-якого дійсного числа x виконується рівність: До 1772 року Ейлер довів, що 2  − 1 = 2 147 483 647 є числом Мерсенна. Правдоподібно, це число було найбільшим відомим простим до 1867 року. 31

Леонард Ейлер портрет Леонарда Ейлера, виконаний Емануелем Гандманном у 1753 р. (перебуває в музеї мистецтва м. Базель) Швейцарські 10 франків з портретом молодого Ейлера Портрет Йогана Георга Брюкера Народився 15 квітня 1707 Базель, Швейцарія Помер 18 вересня 1783 Санкт-Петербург, Росія Місце проживання Королівство Пруссія, Росія Швейцарія Національність Швейцарець Alma mater Базельський університет Відомий у зв'язку з: рівняння Ейлера та інші

Фалес Біографія Наукова спадщина Теорема Фалеса Любомудріє до змісту

Біографія Фале с Міле тський (грец. Θαλῆς ὁ Μιλήσιος, прибл. 624 до н. е. — 548 до н. е.) — давньогрецький філософ досократського періоду, математик, астроном, засновник іонійської школи натурфілософії, купець і політичний діяч. Походив із знатного фінікійського роду. У своїй творчості поєднував питання практики з теоретичними проблемами, що стосувались проблем Всесвіту. Він багато подорожував, зокрема, у молодості відвідав Єгипет, де в школах Мемфіса і Фів вивчав різні науки. Повернувшись на батьківщину, заснував у Мілеті філософську школу. Усі натурфілософські пізнання Фалес використовував для створення завершеного філософського вчення. Так, він вважав, що все існуюче породжене водою. Вода — це джерело, з якого все постійно виникає. При цьому вода й усе, що з неї виникло, не є мертвими, вони живі. Як приклад, Фалес згадував магніт і янтар: вони породжують рух, отже, вони мають душу. Фалес уявляв увесь світ пронизаним життям. Він заклав теоретичні основи вчення, що має назву гілозоїзм. Хоча гілозоїзм має свої корені в міфології, у Фалеса він одержує філософське обґрунтування. Деталі фрески, Фалес Мілетський

Наукова спадщина Фалеса вважають першим грецьким астрономом. Він передбачив сонячне затемнення (28 травня 585 до н. е.). Йому належить заслуга у визначенні часу сонцестояння і рівнодення, у встановленні тривалості року в 365 днів, відкриття факту руху Сонця відносно зірок. У наш час іменем Фалеса названо кратер на видимій стороні Місяця. Фалес також має великі заслуги у створенні наукової математики. У нього вперше в історії математики зустрічаються доведення теорем. Якщо єгипетських землемірів задовольняла відповідь на питання «Як?», то Фалес, мабуть, першим у світі поставив питання «Чому?» й успішно відповів на нього. Нині відомо, що багато математичних правил були відкриті набагато раніше, ніж у Стародавній Греції. Але усі — дослідним шляхом. Строго логічне доведення правильності тверджень на підставі загальних положень, прийнятих за достовірні істини, було винайдено греками. Характерна і зовсім нова риса грецької математики полягає в поступовому переході за допомогою доведення від одного твердження до іншого. Саме такий характер математиці був наданий Фалесом. І навіть сьогодні, розпочинаючи доведення, наприклад, теореми про властивості ромба, ми, по суті, міркуємо майже так само, як це робили учні Фалеса. Вважається, що Фалес першим познайомив греків з геометрією. Йому приписують відкриття і доведення ряду теорем: про поділ кола діаметром навпіл; про те, що кут, вписаний у півколо, є прямим (Теорема Фалеса); про рівність кутів при основі рівнобедреного трикутника; про рівність вертикальних кутів; про пропорційність відрізків, утворених на прямих, що перетинаються декількома паралельними прямими (Теорема Фалеса (пропорційні відрізки)). Фалес установив, що трикутник повністю визначається стороною і прилеглими до неї кутами. Фалес відкрив цікавий спосіб визначення відстані від берега до видимого корабля. Деякі історики стверджують, що для цього він використав ознаку подібності прямокутних трикутників. Фалесу приписують також спосіб визначення висоти різних предметів, зокрема пірамід, за довжиною тіні, коли сонце піднімається над горизонтом на 45 градусів. У «Політиці» Аристотеля знаходиться фрагментарний уривок про те, як Фалес за допомогою астрономічних знань зміг передбачити врожай олив та використати цей факт в цілях власного збагачення, показавши, що філософи здатні стати багатими, хоча цього й першочергово не прагнуть. За те, що він зрозумів вплив дефіциту товарів на процес ціноутворення, його можна вважати також раннім економістом. Усі ці досягнення принесли Фалесу славу першого мудреця серед знаменитих «семи мудреців» далекого минулого.

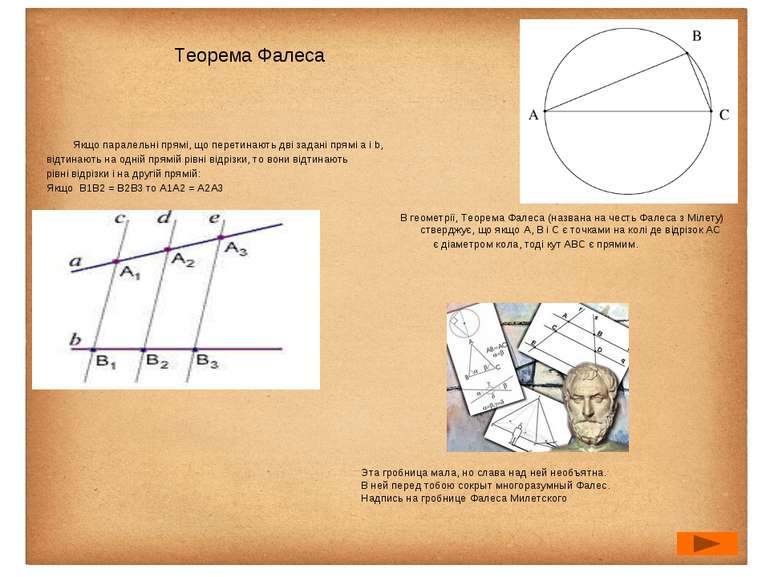
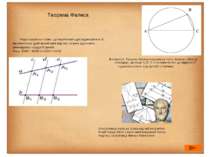
Якщо паралельні прямі, що перетинають дві задані прямі а і b, відтинають на одній прямій рівні відрізки, то вони відтинають рівні відрізки і на другій прямій: Якщо B1B2 = B2B3 то A1A2 = A2A3 В геометрії, Теорема Фалеса (названа на честь Фалеса з Мілету) стверджує, що якщо A, B і C є точками на колі де відрізок AC є діаметром кола, тоді кут ABC є прямим. Эта гробница мала, но слава над ней необъятна. В ней перед тобою сокрыт многоразумный Фалес. Надпись на гробнице Фалеса Милетского Теорема Фалеса

Любомудріє Фалес Блаженство тіла полягає в здоров'ї, блаженство розуму - у знанні. За три речі вдячний я долю: по-перше, що я людина, а не тварина, по-друге, що я чоловік, а не жінка, по-третє, що я еллін, а не варвар. Коли найлегше зносити нещастя? Коли бачиш, що твоїм ворогам ще гірше. Багатослівність ще не запорука розуміння. Мудрішими за все - час, бо воно розкриває все. Треба не з вигляду бути хорошим, а характером пригожим. Чи не зовнішність треба прикрашати, але бути гарним в духовних починаннях. Про друзів має пам'ятати не тільки в присутності їх, але й за відсутності. Пам'ятайте, що діти ваші будуть обходитися з вами так само, як ви обходитеся зі своїми батьками. Нехай ніякі чутки не відвернуть тебе від тих, хто тобі довірився. Найважче - пізнати самого себе, найлегше - давати поради іншим. Сильніше за все - неминучість, бо вона панує над усім. Людину, зводить наклепи на інших, виганяй з дому. Що саме загальне для всіх? Надія, бо якщо у кого більше нічого немає, то вона є.

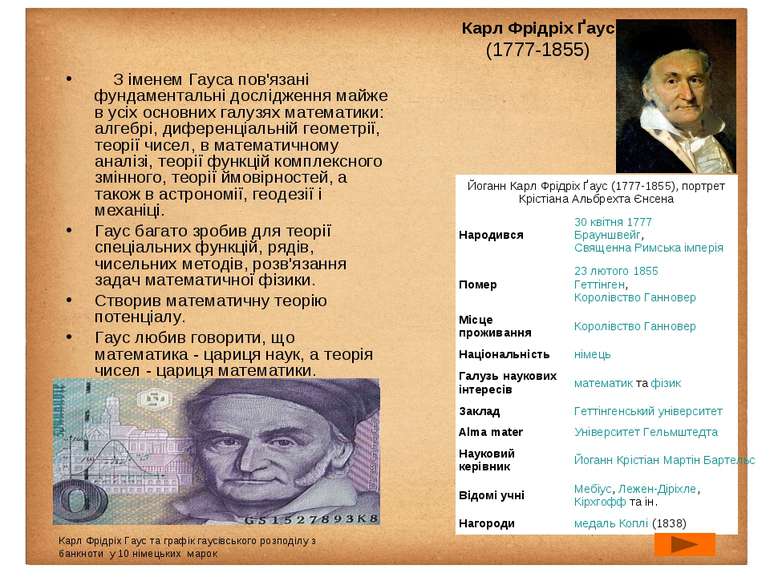
Карл Фрідріх Ґаус (1777-1855)     З іменем Гауса пов'язані фундаментальні дослідження майже в усіх основних галузях математики: алгебрі, диференціальній геометрії, теорії чисел, в математичному аналізі, теорії функцій комплексного змінного, теорії ймовірностей, а також в астрономії, геодезії і механіці. Гаус багато зробив для теорії спеціальних функцій, рядів, чисельних методів, розв'язання задач математичної фізики. Створив математичну теорію потенціалу. Гаус любив говорити, що математика - цариця наук, а теорія чисел - цариця математики. Карл Фрідріх Гаус та графік гаусівського розподілу з банкноти у 10 німецьких марок Йоганн Карл Фрідріх Ґаус (1777-1855), портрет Крістіана Альбрехта Єнсена Народився 30 квітня 1777 Брауншвейг, Священна Римська імперія Помер 23 лютого 1855 Геттінген, Королівство Ганновер Місце проживання Королівство Ганновер Національність німець Галузь наукових інтересів математик та фізик Заклад Геттінгенський університет Alma mater Університет Гельмштедта Науковий керівник Йоганн Крістіан Мартін Бартельс Відомі учні Мебіус, Лежен-Діріхле,Кірхгофф та ін. Нагороди медаль Коплі (1838)

Пам'ятник Гауссу в Брауншвейзі Підпис Гаусса 1777 - 1855 «Не считать ничего сделанным, если ещё кое-что осталось сделать» до змісту

Еварист Галуа (1811-1832)     За 20 років життя французький математик Еварист Галуа встиг зробити відкриття, що поставило його на рівень найвидатніших математиків ХІХ століття. Розв'язуючи задачі з теорії алгебраїчних рівнянь, він заклав основи сучасної алгебри, вийшов на такі фундаментальні поняття, як група (Галуа першим використав цей термін, активно вивчаючи симетричні групи) і поле (скінченні поля носять назву полів Галуа). Відкриття Галуа справили величезне враження і поклали початок новому напрямку математики - теорії абстрактних алгебраїчних структур. Народився 25 жовтня 1811 Помер 31 травня 1832 Париж Місце проживання Париж Громадянство французьке Галузь наукових інтересів математика Заклад Вища нормальна школа Alma mater Вища нормальна школа Відомий у зв'язку з: групи пермутацій, степеневі рівняння

Математичні роботи,які обезсмертили його ім'я, займають трохи більше 60 сторінок. 1811 - 1832 до змісту Медаль Эвариста Галуа

Микола Іванович Лобачевський  (1792-1856) Увійшов як перший учений, який виступив з принципово новою теорією геометрії. М.І. Лобачевський зробив сміливий висновок про те, що можлива геометрія, яка грунтується на запереченні аксіоми паралельності Евкліда. Усе життя він присвятив створенню цієї "уявної геометрії", яка зараз називається геометрією Лобачевського. У цій геометрії до даної прямої через дану точку можна провести нескінченно багато прямих, їй паралельних. Це була справжня революція в науці. "Легше було зупинити Сонце, легше було зрушити Землю, ніж звести паралелі до сходження" (В.Ф.Каган)     Крім геніальних робіт з геометрії вченому належить ряд важливих праць з алгебри та аналізу. Він запропонував точне визначення функції, довів одну з ознак збіжності рядів, установив відмінність між неперервністю та диференційовністю функції. Народився 1 грудня 1792 р. Нижній Новгород Помер 24 лютого 1856 р. Казань Місце проживання Казань Громадянство Російська імперія Галузь наукових інтересів математика Заклад Казанський університет Alma mater Казанський університет Відомий у зв'язку з: один з творців  неевклідової геометрії

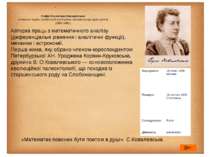
«Математик повинен бути поетом в душі» С.Ковалевська до змісту Біографічна довідка Портретна галерея

Софія Василівна Ковалевська «Небесна муза» (російський математик, письменниця, публіцистка (1850-1891) . Авторка праць з математичного аналізу (диференціальні рівняння і аналітичні функції), механіки і астрономії. Перша жінка, яку обрано членом-кореспондентом Петербурзької АН. Уроджена Корвин-Круковська, дружина В. О.Ковалевського — основоположника еволюційної палеонтології, що походив із старшинського роду на Слобожанщині. «Математик повинен бути поетом в душі» С.Ковалевська Народилася 15 січня 1850 Москва Померла 10 лютого 1891 Стокгольм Громадянство Росія Діяльність математик

Софія Василівна - перша російська жінка-професор математики - народилася 3 січня (за старим стилем) 1850 року в Москві в сім'ї Корвін-Круковських. Батько Софії Василь Васильович, отримавши свідоцтво про дворянство, успадкував подвійне прізвище, що належить до старовинного аристократичного роду; мати Софії Єлизавета Федорівна була онукою петербурзького академіка, астронома Федора Івановича Шуберта і донькою почесного академіка Федора Федоровича Шуберта). Пізніше Софія Ковалевська говорила, що пристрасть до науки вона отримала від предка, угорського короля Матвія Корвіна, любов до математики, музики і поезії від діда Шуберта, вільну і свободолюбиву вдачу - від Польщі, потяг до мандрування і невміння підкорятися загальноприйнятим звичаям - від прабабки циганки, а все інше - від Росії. КОВАЛЕВСЬКА Софія Василівна (1850 - 1891) - російський математик, письменниця, перша російська жінка-професор. У 1888 р. Паризька академія наук оголосила третій конкурс на найкращу працю з цієї теми з видачею премії Бордена на три тисячі франків. Перші два конкурси не дали очікуваних результатів, і премію нікому не присудили. Софія Василівна надіслала свою роботу на конкурс, узявши за девіз французьку приказку: «Говори, що знаєш, роби, що повинен; що буде, те й буде”. На конкурс було подано 15 праць. Спеціальна комісія Паризької академії визнала, що твір під девізом «Говори, що знаєш», відмінний, що в ньому відкрито новий випадок. Враховуючи всі наукові якості цієї праці, комісія ухвалила присудити авторові твору збільшену премію: замість трьох тисяч — п'ять тисяч франків. Ця праця була надрукована в наукових записках Паризької академії наук за 1889 рік. Вчені не поскупилися на оплески. Софія Василівна, настільки була приголомшена успіхом, насилу опанувала себе і вимовила слова подяки.

Монета Банка России — Серия: «Выдающиеся личности России», 150-летие со дня рождения С.В. Ковалевской, 2 рубля Бюст великого русского математика на её малой родине – в селе Полибино Великолукского района

Андрій Миколайович Колмогоров  (1903 - 1987)       Видатний радянський математик, доктор фізико-математичних наук, професор Московського державного університету (1931), академік Академії Наук СРСР (1939). Отримав міжнародне визнання - був почесним членом багатьох іноземних академій і наукових товариств. Колмогоров - один із основоположників сучасної теорії ймовірностей, ним отримані фундаментальні результати в топології, математичній логіці, теорії турбулентності, теорії складності алгоритмів і цілому ряді інших областей математики і її застосувань.     А.М.Колмогорова по праву вважають одним з найвидатніших учених ХХ століття.

1903 - 1987 до змісту

Піфагор Середньовічна гравюра, що зображає Піфагора зі дзвониками для побудови звукоряду для настроювання музичних інструментів Наукові досягнення. Теорема Піфагора. Біографічна довідка Піфагорові штани Любомудріє до змісту

Наукові досягнення Піфагор займає почесне місце в історії математики. Він відкрив нову епоху в еволюції наукової думки. Піфагорійці перетворили давно відомі практичні правила в наукові положення, обґрунтовані точними доведеннями. Піфагор увів загальновизнаний тепер дедуктивний метод, суть якого полягає в тому, що, крім невеликої кількості прийнятих без доведень первісних положень, які називаються аксіомами, всі інші твердження математики виводяться логічними міркуваннями. Вчення про число Основним змістом піфагорійської математики є вчення про число. Як і вавилонські маги, піфагорійці вважали надзвичайно важливими різні властивості чисел і відношення між ними. І коли відсіяти полову — числову містику, виявиться, що вони ввели багато фундаментальних теоретико-числових понять, виявили і дослідили глибокі властивості чисел і поставили такі питання, які й сьогодні залишаються предметом досліджень багатьох учених і все ще чекають свого розв’язання. Досконалі числа Найважливішою властивістю чисел піфагорійці вважали парність і непарність і першими ввели поняття парного і непарного числа, простого і складеного, розробили теорію подільності на два, дали кілька класифікацій натуральних чисел. Піфагорійці вважали унікальними такі числа, в яких сума власних дільників, тобто дільників, менших від самого числа, дорівнює самому числу. Наприклад: 6 = 1 + 2 + 3, 28 = 1 + 2 + 4 + 7 + 14. Піфагорові трійки

Піфаго р — давньогрецький філософ, релігійний та політичний діяч, засновник піфагореїзму  став легендою і джерелом дискусій уже в стародавні часи. Піфагор жив у шостому столітті до нашої ери, мав гарну зовнішність, носив довгу бороду, а на голові золоту діадему. Піфагор - це не ім`я, а прізвисько, яке філософ отримав за те, що завжди говорив вірно і переконливо, як грецький оракул. (Піфагор - "переконує промовою".) Був він філософом ідеалістом та видатним математиком. Піфагор, а ще його називають Піфагором Самосським, був учнем Анаксимандра - старогрецького філософа, представника Мілетськой школи (заснованою в Мілете Фалесом - першим старогрецьким філософом, йому належать вчення про природу, про воду, про різні форми і стани речовин). З юного віку Піфагор тягнувся до знань і подорожей. У 18 років він покинув рідний острів і відправився в чужі краї. Він побував на Сході в Єгипті, Вавилоні і Фінікії. У самому Єгипті, він прожив близько 22 років, де за деякими даними осягав таємні езотеричні учення жерців - «присвячених», а так само вивчав астрономію, математику і інші науки. Спеціально для цього Піфагор вивчив єгипетську мову. Із написаних творів Піфагора відомі «Про виховання», «Про природу», «Про світ», «Про державу», «Про душу». Найбільш відомим фактом сьогодення про Піфагора – є всього одна фраза: "Піфагорові штани на всі сторони рівні". Πυθαγόρας Народився пр. 580 – 572 до н. е. на острові Самос. Батько благородного походження Помер пр. 500 – 490 до н. е. Школа/Традиція піфагорейство Основні інтереси метафізика, музика,математика, етика, політика Значні ідеї Musica universalis, золотий перетин, піфагорейський лад,теорема Піфагора

Улюбленою геометричною фігурою піфагорійців була пентаграма або піфагорова зірка.При зустрічі вони малювали її на піску - вітаючись один з одним. Пентаграма служила їм паролем і була символом здоров'я і щастя.

Піфаго рові штани (шкільне, застаріле) — жартівлива назва одного з доведень теореми Піфагора. В старих шкільних посібниках наводилось доведення теореми через отримання рівності суми площ квадратів, побудованих на катетах прямокутного трикутника, площі квадрата, побудованого на гіпотенузі цього трикутника.Побудовані на сторонах трикутника, розбіжні квадрати нагадують покрій чоловічих штанів Побудова «Піфагорових штанів» Піфагорійська трійка: 3 + 4 = 5. Піфагор, людина в центрі, з книгою, викладання музики в Афінській школі Рафаель Монета з зображенням Піфагора

Словомудріє Філософське вчення Введення терміну «філософ» приписують Піфагору, який назвав себе не мудрецем, а «тим, хто любить мудрість». Філософи належать до особливого типу людей, які замість того, щоб турбуватися про славу чи визнання, гроші чи прибуток, все життя присвячують вивченню природи речей. Про Всесвіт Піфагор був першим, хто назвав Всесвіт «Космосом» через ту впорядкованість, яка йому притаманна. За його вченням основоположні принципи світобудови можна висловити мовою математики. Початком, що об'єднує всі речі, виступають числові співвідношення, які виражають гармонію й порядок природи: «Всі речі суть числа». Всесвіт, за Піфагором, — шароподібний і складаєть з десяти небесних сфер. В центрі Всесвіту розташований невидимий із землі «вогонь», який піфагорійці називають «стражем Зевса». Навколо нього обертаються всі сфери, в тому числі й Земля. Кожна сфера є визначена числом і дає притаманний лише їй звук, в результаті космос в цілому являє собою гармонійний світовий хор Про Бога За вченням Піфагора, «Бог — це число чисел», це єдиний Бог, що містить в собі все. Бог виявляється як закон і сам є закон. А прийняття цього Закону — Клятва слухняності закону. Піфагорійці, даючи клятву, були впевнені, що справа, яку вони обіцяють виконати, освячена божественним Законом. Клятва: «Клянуся ім'ям Тетрактис, що послана нашим душам. В ній джерело й корені вічно квітнучої природи». Про сакральну математику У своєму прагненні осягнути вічну Істину Піфагор звертався до математики, вважаючи цю священну науку найкращим методом для осягнення й висловлення першопринципів, об'єднуючої сили космосу. З цієї точки зору, усе створене прив'язане до числових правил і пропорцій, які синтезовані числі десять — досконалому числі. До заслуг Піфагора (швидше, членів його ордену, оскільки в більшості випадків винаходи останніх за звичаєм приписувалися Піфагору) належить відкриття та доведення теореми Піфагора- однієї із ґрунтовних теорем евклідової геометрії. Про гармонію Гармонія присутня скрізь у Всесвіті: і в комбінації ритмів астрономічних тіл, за якими вони обертаються в просторі, відомій як «музика сфер», і в мистецтві музики, яка очищує душу. Гармонія встановлена не лише на фізичному рівні, але також і в зв'язках між космічним і моральним порядком. Піфагор увів звичай застосовувати музику для очищення душі й практикував лікування музикою. Деякі мелодії були проти пригнічуючих душу страждань — смутку й мук, другі — проти гніву й злості, а треті — проти пристрастей. Піфагорейцями було відкрито гармонійні співвідношення октави, квінти й кварти, а також числові закони, що ними керують. Про дружбу Піфагорійці високо цінували дружбу, яка розглядалась як невід'ємна умова спільного життя, що добре ілюструє відомий вислів: «між друзями всі речі — спільні». Піфагорійська дружба досі слугує гідним прикладом відданих, чесних, щирих стосунків між людьми. Про перевтілення душі За Піфагором, душа є безсмертною та перевтілюється після смерті в інші живі істоти, зокрема, у тварин. Грецький філософ Ксенофан висміював це бачення: «Одного разу Піфагор проходив біля людей, які знущалися з собаки. „Не бийте його. Це душа одного мого друга. Я впізнав її по голосу.“»

Використані джерела http://uk.wikipedia. http://www.greatmath.net http://www.krugosvet.ru http://ru.wikipedia.org/wik http://images.yandex.ru Арнольд В.И., Гюйгенс и Барроу, Ньютон и Гук. М., Наука, 1989 БОРОДИН А. И., БУГАЙ А. С. Биографический словарь деятелей в области математики / Пер. с укр. — Киев : Радянська школа, 1979. — С. 131—134. Белл Е. Т. Творці математики. М.: Просвіта, 1979, 256 c., глава 15. Васильєв О. В. Микола Іванович Лобачевський. — М.: Наука. 1992. — 229 с (Науково-біографічна серія). Глейзер Г. І. Історія математики в школі. — М.: Просвіта, 1964. — С. 345-350. Житомирский С. В. Архимед: Пособие для учащихся. М.: Просвещение, 1981. Українська радянська енциклопедія. У 12-ти томах. / За ред. М. Бажана. — 2-ге вид. — К., 1974—1985. Паскаль Б. Думки // Філософська думка, 2008, № 5. — С. 101—118. Шмигевський М. В. Видатні математики. — Бібліотека журналу «Математика в школах України»; випуск 6 (18). — Харків : «Основа», 2004. — 176 с.