Презентація на тему:
Розкриття дужок

Історія виникнення раціональних чисел

Назву числа колись показували на пальцях Так починали навчатись користуватись там, що дала людині природа – власними пальцями

Навчатись рахувати вимагало життя Потрібно було знати, чи вистачить здобичі до наступного полювання, Чи багато упіймали риби

Спочатку лише деякі числа мали назви Називаючи число 1, виходили з того, що сонце у небі одне

Назву числа 2 найчастіше пов’язували із парними органами крильми очима руками

«Три та чотири – разом сім» люди отримали, помітивши що ківш Великої Ведмедиці, складається із трьох зірок ручки та ще чотирьох зірок

А далі люди почали рахувати десятками Пальці виявились чудовою обчислювальною машиною, за їх допомогою можна було рахувати до 5 А якщо взяти дві руки – то і до 10 В країнах, де люди ходили босоніж легко можна було рахувати і до 20

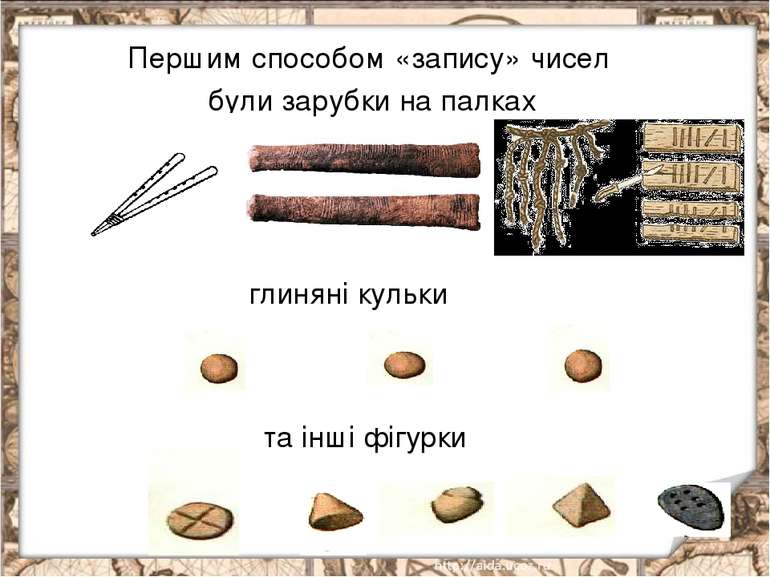
Проходили роки, мінялось життя людей Виникла потреба записувати числа Люди приручали тварин, почали займатись скотарством

Першим способом «запису» чисел були зарубки на палках глиняні кульки та інші фігурки

Індійці в Америці зображали числа за допомогою вузликів на мотузці

Давній Єгипет 15 Числа першого десятку записували відповідною кількістю паличок

Давній Єгипет Не дуже зручно було записувати таким чином числа і зовсім незручно їх додавати, віднімати, множити та ділити

Всі числа складались із сполучення клинців. Вертикальна риска означала одиницю, а кут з двох лежачих рисок – десять В давньому Вавілоні записували числа, видавлюючи значки клинком на глиняній дощечці

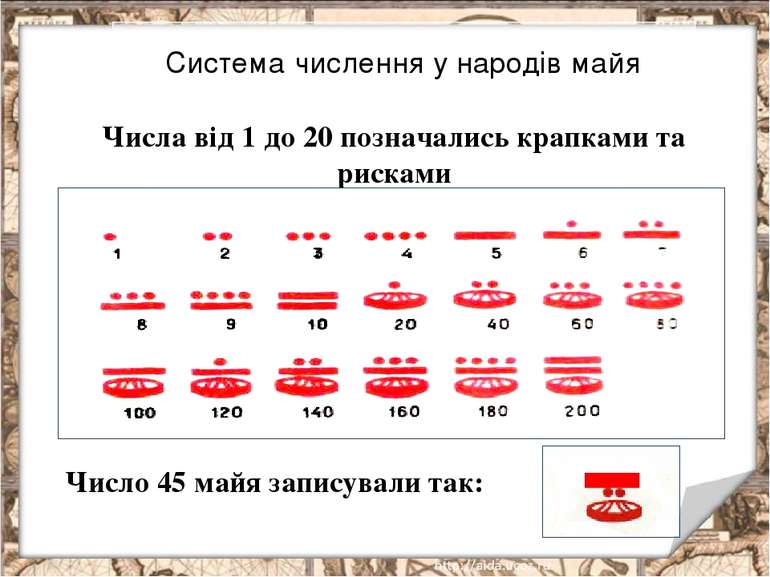
Числа від 1 до 20 позначались крапками та рисками Число 45 майя записували так: Система числення у народів майя

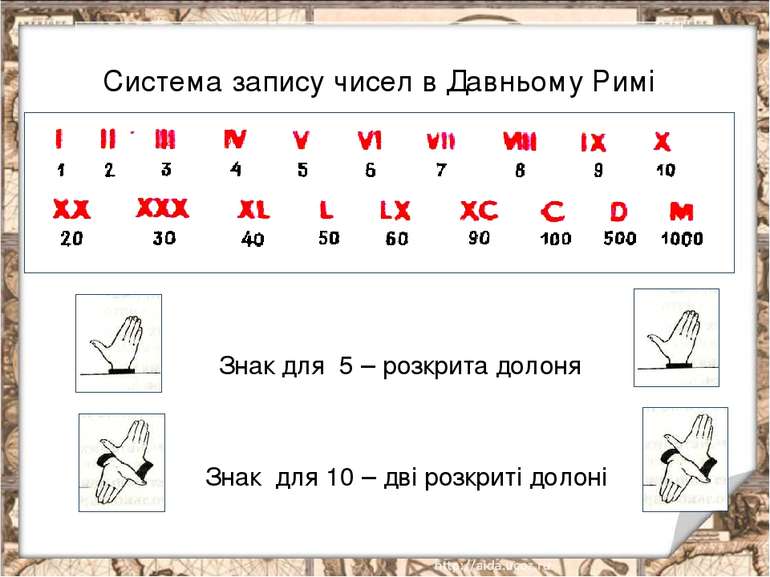
Система запису чисел в Давньому Римі Знак для 5 – розкрита долоня Знак для 10 – дві розкриті долоні

Давньоруський запис чисел В Древней Руси буква «а» обозначала число 1 Буква «б» обозначала число 2 Для обозначения чисел 10, 20,100,…, 900 использовались буквы. Для отличия букв от слов использовали знак титло Словянські цифрові знаки – літери з титлами

Натхнення при вивченні теми!

Історія виникнення від’ємних чисел

Стародавній Китай Від'ємні числа були відомі китайським вченим приблизно ІІ ст. до н.е. Додатні кількості в китайській математиці назвали «чен», від’ємні — «фу»; їх зображали різними кольорами: «чен» — червоним, «фу» — чорним. Такий спосіб зображення використовувався в Китаї до середини XIII ст., поки Лі Є не запропонував зручніше позначення від’ємних чисел — цифри, що зображали від’ємні числа, перекреслювали рискою навскіс справа наліво.

Стародавня Індія У V—VI ст. від’ємні числа поширюються в індійській математиці. В Індії від’ємні числа систематично застосовували і тлумачили в основному так само, як це ми робимо тепер. Уже в творі Брамагупти «Перегляд системи Брами» (628 р.) ми читаємо: «Майно» і «майно» є «майно», сума двох «боргів» є «борг»; сума «майна» і нуля є «майно»; борг, який віднімають від нуля, стає «майном», а «майно» — «боргом». Якщо треба відняти «майно» від «боргу», а «борг» від «майна», то беруть їх суму…». Про те, як індійські вчені відкрили від’ємні числа, достовірно ми нічого не знаємо.

Європа В Європу від'ємні числа проникали важко. Німецькі вчені спочатку називали їх "числами від сатани", "абсурдними числами", бо "в них усе навпаки: додавання їх зменшує суму, а віднімання збільшує." Сучасне позначення додатних і від'ємних чисел із знаками "+" та "-" ввів наприкінці XV ст. німецький математик Відман. Однак і після цього багато математиків не визнавали їх.

У розробці питань, пов'язаних з від'ємними числами, велику роль  відіграла праця математика Михайла Васильовича Остроградського. Він народився на Полтавщині 1801 року. Розповідають, що вже в дитинстві він завжди ходив із шнурком у кишені, прив'язавши до нього камінець, за допомогою якого вимірював глибину всіх криниць. Остроградський навчався в гімназії, в Харківському університеті на механіко-математичному факультеті. У 1822 році він їде до Парижа, де привертає до себе увагу французьких учених. Його вважали науковим авторитетом у галузі математики і механіки, символом стійкості та енергії. М. В. Остроградський був чудовим учителем, він писав: "КРАЩЕ ВЧИТЬСЯ НЕ ТОЙ, ХТО СТАРАННО ЗАПАМ'ЯТОВУЄ ПРОЧИТАНЕ, А ТОЙ, ХТО НАБУВАЄ ВМІННЯ ВИКОРИСТАТИ ЙОГО". В європейській науці від'ємні числа почали широко застосовувати тільки із часів великого французького вченого Рене Декарта, який у книжці "Геометрія" зобразив від'ємні числа за допомогою "монорейкової дороги", тепер ми її називаємо координатною прямою.