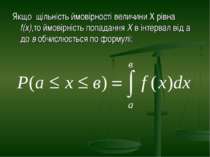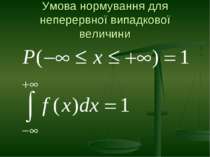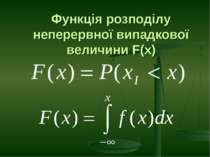Презентація на тему:
Основи теорії ймовірності та математичної статистики
Завантажити презентацію
Основи теорії ймовірності та математичної статистики
Завантажити презентаціюПрезентація по слайдам:
План лекції Основні поняття теорії ймовірностей Теорема додавання та множення Дискретна випадкова величина Числові характеристики дискретних та неперервних випадкових величин Генеральна та вибіркова сукупності. Точкові оцінки параметрів розподілу. Інтервальні оцінки параметрів розподілу
Основні поняття теорії ймовірностей Теорія ймовірностей вивчає масові випадкові події, які характеризуються стійкою частотою їх появи. Випадковою подією в теорії ймовірності називають всякий факт, який в результаті досліду (спостереження) може відбутися або не відбутися. Різні випадкові події позначаються латинськими буквами А, В, С… .
Несумісні події Події являються несумісними, якщо при дослідженні дві з названих подій не можуть одночасно спостерігатись (при одному вимірювані тиск не може бути нормальним і підвищеним).
Протилежні та рівноможливі події Дві несумісні події, які складають повну групу подій називаються протилежними. Події називають рівноможливими, якщо ймовірності їх спостереження рівні.
Достовірна та неможлива події Найбільшу ймовірність, яка рівна 1, має достовірна подія, тобто така, яка обов'язково буде спостерігатися в результаті досліду. Найменша ймовірність, яка рівна 0 у неможливої події, тобто такої яка не може спостерігатися в даному досліді.
Незалежні події Подія А називається незалежною від події В, якщо ймовірність події А не залежить від того відбулась подія В чи не відбулась. Наприклад, група крові у другого донора не залежить від того яка група крові була у першого донора.
Залежні події Подія А називається залежною від події В, якщо ймовірність спостереження події А залежить від того відбулась подія В чи така подія не відбулась. В такому випадку ймовірність події А обчислена при умові, що мала місце подія В називається умовною ймовірністю події А і позначається Р(А/В).
Теорема множення Якщо події А і В незалежні, то ймовірність складної події, яка складається із двох подій А і В рівна добутку ймовірності цих подій Р(А і В)=Р(А) Р(В) Якщо події А і В залежні, то ймовірність складної події рівна добутку ймовірності однієї з них на умовну ймовірність іншої. Р(А і В)=Р(А)·Р(В\А)=Р(В)·Р(А\В)
Випадкова величина Випадкова величина - це величина, яка приймає в результаті випробувань одне з багатьох можливих значень, причому появу того чи іншого значення передбачити неможливо, тобто воно являється випадковою подією. Розрізняють дискретні і неперервні величини
Дискретна випадкова величина Це така випадкова величина, яка може приймати кінцеву кількість значень на заданому інтервалі, тобто таку множину, елементи якої Х можуть бути занумеровані в якомусь порядку і виписані в послідовності Х1, Х2, Х3, ….,Хn. Випадкова величина вважається заданою, якщо заданий закон її розподілу.
Неперервна випадкова величина Це така випадкова величина, яка може приймати будь-яке із значень, які належить до даного інтервалу. Неперервна випадкова величина приймає нескінчену кількість значень, ймовірність того, що вона прийме якесь конкретне значення рівна нулю.
Якщо щільність ймовірності величини Х рівна f(x),то ймовірність попадання Х в інтервал від а до в обчислюється по формулі:
Математичне сподівання неперервної випадкової величини Математичним сподіванням неперервної випадкової величини Х усі можливі значення якої належать скінченному відрізкові [a;b] називається визначений інтеграл
Дисперсія неперервної випадкової величини Дисперсією неперервної випадкової величини називається математичне сподівання квадрату її відхилення від математичного сподівання:
Елементи математичної статистики Математична статистика - це розділ прикладної математики, який безпосередньо примикає до теорії ймовірності. На відміну від теорії ймовірності математична статистика розглядає не дії над законами розподілу і числовими характеристиками випадкових величин, а наближені методи встановлення цих законів по результатах експерименту.
Генеральна та вибіркова сукупності Спостереження над біологічними об’єктами ведеться за певною ознакою, яка змінюється при переході від одного члена сукупності до іншого. Зміну цієї ознаки називають варіацією, а значення ознаки у даного члена статистичної сукупності - його варіантою X. Так у новонароджених дітей вага являється варіантою, яка варіює від дитини до дитини.
Статистична сукупність, яка включає в себе всі можливі члени, які в принципі можуть бути віднесені до даної сукупності, називається генеральною. Генеральну сукупність складають всі жителі міста, хворі з даним діагнозом. Внаслідок її багаточисленості генеральна сукупність для дослідження важкодоступна. Тому досліджують частину об’єктів із генеральної сукупності, яку називають вибірковою сукупністю, або вибіркою.
Для того щоб вибірка достатньо точно характеризувала властивості генеральної сукупності, вибірка повинна бути репрезентативною. Вибірка буде репрезентативною, якщо всі об’єкти генеральної сукупності будуть мати однакову ймовірність потрапити у вибірку.
Точкові оцінки параметрів розподілу Одним з основних завдань математичної статистики є визначення характеристик генеральної сукупності по дослідженням вибіркової сукупності і встановлення того, наскільки параметри вибірки відображають основні характеристики генеральної сукупності.
Точкове оцінювання. Точковою оцінкою називають таку оцінку, яка визначається одним числом. Точкові оцінки повинні мати властивості, які задовольняють певні вимоги: 1. Незміщеність - математичне сподівання оцінки дорівнює оцінюваному параметру генеральної сукупності при будь - якому об’ємі вибірки.
2. Ефективність - серед можливих незміщених оцінок вибирають ту, яка має найменшу дисперсію. 3. Обґрунтованість - з ймовірністю, близькою до одиниці, різниця між істинною величиною параметра та значенням його оцінки є як завгодно малою при достатньо великому об’ємі вибірки.
Інтервальні оцінки Інтервальною називають таку оцінку яка визначається двома числами - кінцями інтервалу, який покриває оцінюваний параметр. Інтервальні оцінки дозволяють встановити точність і надійність оцінок.
Довірчим називають інтервал, який із заданою надійністю α покриває заданий параметр. Величина α повинна бути достатньо близькою до 1. В біологічних дослідженнях довірча ймовірність повинна бути рівною 0,95 (95%). При розробці біологічних стандартів потрібно користуватись 99%-ю довірчою ймовірністю.
Схожі презентації
Категорії