Презентація на тему:
Математика в музиці

Проект Музыка и математика Автор работы: Григорьева Снежана Ученица 8Б класса

Наверняка, каждый из вас сейчас подумал, какая же связь может быть между математикой - мудрой царицей всех наук, и музыкой? Как могут воздействовать, такие, совершенно разные человеческие культуры? И сегодня в моей работе, я предлагаю вам найти ответы на эти вопросы. И попробую доказать, что связь между музыкой и математикой всё же  существует

Тема моего исследования - «Музыка и математика в цифрах». Математика и музыка – два школьных предмета, два полюса человеческой культуры. Слушая, музыку мы попадаем в волшебный мир звуков и открываем в ней совершенство, простоту и  гармонию. Решая математические задачи,  мы погружаемся в строгое пространство чисел. И не задумываясь о том, что мир звуков и пространство чисел издавна тесно связаны друг с другом. И что если попробовать определенным образом переложить ноты на числа. Будет ли наблюдаться в этом числовом ряду закономерность? Если такая связь существует, то можно предположить обратное, что ряд чисел имеет свое музыкальное звучание. В этом и актуальность моего исследования.

В своей работе я выдвинула следующую гипотезу: Любое музыкальное произведение   можно представить, как некую математическую модель. Объект исследования: музыка и математика. Предмет исследования: энциклопедии, словари, художественная и научная литература, периодическая  печать, тезисы с Интернета.

1.История исследования связи музыки с математикой. Математика – царица наук, тесным образом перекликается с музыкой. Несомненно, математика пронизывает музыку. Музыка и ее первый звук родились одновременно с творением мира, как  утверждали древние мудрецы.

В своих трудах ученые неоднократно делали попытки представить музыку как некую математическую модель. Приведем, к примеру, одну из цитат из работы Леонарда Эйлера "Диссертация о звуке", написанная в 1727 году.  "Моей конечной целью в этом труде было то, что я стремился представить музыку как часть математики и вывести в надлежащем порядке из правильных оснований все, что может сделать приятным объединение и смешивание звуков» 1. Свое отношение к математике и музыки ученые  высказывались в своих личных переписках. Так, к примеру, Лейбниц в письме Гольдбаху пишет: "Музыка есть скрытое арифметическое упражнение души, не умеющей считать» 2.На что Гольдбах ему отвечает: "Музыка - это проявление скрытой математики»

Однако, одним из первых, кто попытался выразить красоту музыки с помощью чисел, был Пифагор. Он создал свою школу мудрости, положив в ее основу два предмета - музыку и математику. Музыка, как одно из видов искусств, воспринималась наряду с арифметикой, геометрией и астрономией как научная дисциплина, а не как практическое занятие искусством.

Пифагор считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга. Он был не только философом, но и математиком, и теоретиком музыки. Родился Пифагор около 570 года до нашей эры на острове Самосее. Пифагор основал науку о гармонии сфер, утвердив ее, как точную науку. Известно, что пифагорейцы пользовались специальными мелодиями против ярости и гнева. Они проводили занятия математикой под музыку, так как заметили, что она благотворно влияет на интеллект.

Он учился музыки в Египте и сделал ее предметом науки в Италии. Пифагор считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга. Одним из достижений Пифагора и его последователей в математической теории музыки был разработанный ими «Пифагоров строй». Новая технология использовалась для настройки популярного в то время инструмента – лиры. Тем не менее, «Пифагоров строй» был несовершенен, как и древнегреческая арифметика. Расстояние между соседними звуками «Пифагорова строя» неодинаковые. Он – неравномерный. Чтобы сыграть мелодию, от какой- либо другой ноты, лиру каждый раз нужно перенастраивать.

Исследованию музыки посвящали свои работы многие величайшие математики, такие как: Рене Декарт ( его первый труд  - "Compendium Musicae" в переводе "Трактат о музыке") , Готфрид Лейбниц, Христиан Гольдбах, Жан Д'Аламбер, Даниил Бернулли и другие. «Раздумывая об искусстве и науке, об их взаимосвязях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая и духовная деятельность человека. Что между ними размещается все, что человечество создало в области наук и искусства» - писал Г. Нейгауз. 

Изучив работы ученых мною было установлено, что в прошлом были неоднократные попытки рассматривать музыку, как один из объектов изучения математики. Таким образом,  многие учёные в древности считали, что гармония чисел является сродни гармонии звуков  и  дополняет  друг друга, музыку и математику. __________________________________________________________

2.Исследования музыкальных произведений. 2.1Рассмотрим, к примеру, произведение  Г. Гладкова «Бременские музыканты» (см. приложение 1). (Звучит музыка) Попробуем сделать  математическую модель этого произведения: Каждой ноте мы присвоили номер ступени. Цифра 1 – I ступень, 2 – II ,3 – III, 4 – IV, 5 – V ,6 – VI ,7 – VII, 8 – I, 9 – II ,0 – III.

Переложили ноты на числа и получили при этом такой ряд чисел: 11123313/535/44432246/545/3353/666716/22217572/176/4561/7672/321117/  176213/ 444443/ 22221//. Черта между цифрами служит тактовой четой, то есть делит их на такты, так как сделано в произведении. В музыке есть понятие - устойчивые ступени, на которых  строится тоническое трезвучие (Т5/3): 1, 3, 5 ступени. Если в каждом полном такте сложить номера устойчивых ступеней, то мы заметим следующую закономерность. В первом такте сумма равна 13 (1+1+1+3+3+1+3), во II – тоже 13 (5+5+3), в III – 3 (3), в IV – 10 (5+5), в V – 14  (3+3+5+3), в VI  - 1, в VII – 6 (5+1), в VIII – 1, в IX – 6 (5+1), в X – 0, в XI – 6 (3+1+1+1), в XII – 4 (1+3), в XIII – 3, в XIV – 1.

Получили ряд чисел: 13, 13, 3, 10, 14, 1, 6, 1, 6, 0, 6, 4, 3, 1. Вывод: Следовательно, наблюдаем, что в произведении повторяется группа цифр: 14, 13, 10, 6, 4, 3 ,1, 0.

Теперь попробуем перемножить в каждом такте номера ступеней. Получили числа в соответствии с номерами тактов: I.   54 (1x1x1x2x3x3x1x3). II. 75 (5x3x5) III. 18432 (4x4x4x3x2x2x4x6) IV.100 (5x4x5) V. 135 (3x3x5x3) VI. 9072 (6x6x6x7x1x6) VII. 3920 (2x2x2x1x7x5x7x2) VIII. 12 (1x7x6) IX. 120 (4x5x6x1) X. 288 (7x6x7x2) XI. 336 (3x2x2x2x2x7) XII. 252 (1x7x6x2x1x3) XIII. 3072 (4x4x4x4x4x3) XIV. 16 (2x2x2x2x1)

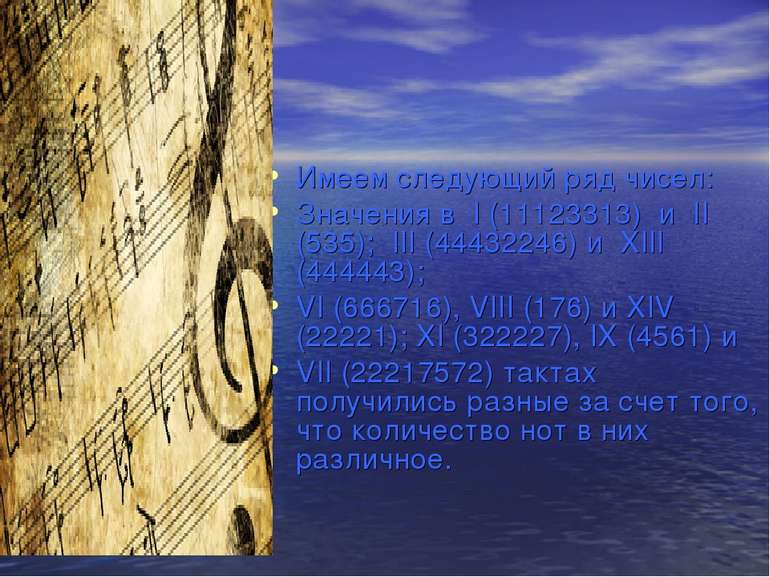
Имеем следующий ряд чисел: Значения в  I (11123313)  и  II (535);  III (44432246) и  XIII (444443);   VI (666716), VIII (176) и XIV (22221); XI (322227), IX (4561) и   VII (22217572) тактах получились разные за счет того, что количество нот в них различное.

Следовательно, наблюдаем, что в произведении повторяется группа цифр: 44 и 2. Теперь попробуем перемножить в каждом такте номера ступеней. Получили числа в соответствии с номерами тактов: I. 455625 (1x3x5x1x3x5x1x3x1x3x5x1x3x5x1x3) II. 21233664 (1x2x6x2x4x6x2x4x1x2x6x2x4x6x2x4) III. 501760000 (7x2x5x2x4x5x2x4x7x2x5x2x4x5x2x4) IV. 455625 (1x3x5x1x3x5x1x3x1x3x5x1x3x5x1x3) V. 136948896 (1x2x6x3x6x6x3x6x1x3x6x3x6x6x3x6) VI. 21233664 (1x2x6x2x4x6x2x4x1x2x6x2x4x6x2x4

3.Исследование дат рождений. Следуя теории Пифагора, числа обладают абсолютной властью над всеми событиями, над всеми живыми существами, а значит, что числа правят музыкой.  В своих работах он утверждал, что музыка подчиняется высшему закону (математике) и вследствие этого восстанавливает в организме человека гармонию. Нумерология – паранаука о числах. Нумерология имеет еще одно распространенное название – Магия Чисел. В нумерологии все слова, имена, числа можно свести к единичным разрядам (однозначным числам), которые соответствуют оккультным характеристикам, влияющим на жизнь человека. Это значит, что каждому числу, согласно нумерологии, соответствуют определенные свойства, образы и понятия. Нумерологию используют для определения характера человека, его природных способностей, для выявления сильных и слабых сторон его личности, а также для определения подходящей профессии, места проживания и многих других факторов.

Даты рождения – это ряд чисел. Попробуем установить связь между числами и музыкой. Мною были  исследованы даты рождения 8 учащихся  8 «а» класса, в котором я обучаюсь. Как известно дата – набор цифр. Мы переложим даты на ноты. У каждого человека получилось по одному аккорду (см. приложение аккордов). Были аккорды звучащие гармонично и вовсе безобразно и резко (в музыке гармоническое звучание тонов называется консонансом. А безобразное, резкое звучание  называется диссонансом.  На рисунке, где под аккордом стоит знак «-», аккорд звучал негармонично, а значит, звучит диссонанс. А если мелодично, то знак «+» - это консонанс. Каждой ноте мы присвоили номер ступени. До – 0, ре – 1. ми – 2, фа – 3, соль – 4, ля – 5, си – 6. до – 7, ре – 8, ми – 9.

После того, как мы переложили даты рождения на аккорды, попробуем установить связь между звучанием даты рождения и способностями человека. Таким образом, 8 учащихся  8 «а» класса, по звучанию разделились на две группы. Методом опроса я выяснил, чем каждый ученик увлекается. Таким образом, мы получили следующее: I группа (дети, у которых аккорды благозвучные): Евгения Оханова 26.07.1997 год (играет на фортепиано и поёт) Алимпиев Андрей  02.09.1997 года Бобренок Валерия 10.09.1997 год (танцует) Баранов Сергей 29.06.1997 года ( занимается в драмкружке) Павская Анастасия 22.05.1997 года (танцует) II группа (дети, у которых аккорды не звучат): Савинков Максим 21.08.91 года (занимается спортом) Басаргина Карина14.10. 1997 года ( занимается спортом) Макаренко Владислав 18.06.1997 года

В первой группе, где аккорды звучали мелодично, оказалось большинство детей с творческими наклонностями:  некоторые из них занимаются в музыкальной школе или танцами. Данная группа детей обладает творческими способностями, косвенно или напрямую связаны с музыкой. Во второй группе, где аккорды звучали «резко», большинство детей занимаются различными видами спорта. Следует отметить, что в двух  группах оказались те, кто по тем или иным причинам ничем не увлекается и не занимается в каких либо секциях. Предполагаю, что возможно, они имеют эти склонности, но еще не реализовали их.  

4.Заключение.  В своей исследовательской работе я  выдвинула  гипотезу о том, что любое музыкальное произведение можно представить как математическую модель, которая будет иметь числовые закономерности. По изложенному в работе способу перевода из нот в числовой ряд следует, что моя гипотеза верна,  так как способов перевода может быть несколько. В работе мы рассмотрели два способа: это  сложение устойчивых ступеней и произведения устойчивых ступеней.  Однако, в ходе выполнения исследования музыкальных произведений, выше перечисленные  способы  мною  выявлено, что не каждый числовой ряд имеет такую математическую  закономерность. Таким примером является музыкальное произведение «Бременские музыканты».

В своей работе я провела исследование дат рождений одноклассников. То, что музыка отражает в себе закономерность числового ряда и как следствие имеется связь между звучанием дат рождений и наклонностями человека находит подтверждение в моем исследовании. Но для утверждения того, что звучание даты рождения определяет определенный тип особенностей человека, необходимо большее количество исследуемых. Если в последующем, при более глубоком и многочисленным исследовании, наше предположение будет доказано, это даст человеку еще один способ открыть себя, определить род занятий, выбрать профессию, где наиболее полно раскроется потенциал личности. В заключение  нашего исследования, мне хочется процитировать  слова известного философа, математика 19-20 вв. Бертрана Рассела «Математика владеет не только истиной, но и высшей красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства».