Презентація на тему:
"Квадратичні нерівності"

Квадратичні нерівності Виконала: учениця 9-А класу КЗО ДСЗШ №147 ім. В. Чорновола Іващенко Ірина

Зміст 1.Що таке квадратна нерівність? 2.Приклад квадратної нерівності 3. Що таке квадратний тричлен? 4.Що таке квадратична функція? 5.Схема побудови квадратичної функції. 6.Приклад квадратичної функції. 7.Метод Інтервалів. 8. Рівняння, що зводяться до квадратних. 9.Розв`язування систем рівняннь.

Що таке квадратна нерівність? Якщо лівою частиною нерівності є вираз виду ах²+bx+c , де а не дорівнює 0 , b, c — дані числа, а правою — нуль, то таку нерівність називають квадратною нерівністю. Квадратні нерівності зручно розв’язувати за допомогою графіків квадратичних функцій. Для цього треба: 1) знайти корені тричлена ах²+bx+c або з’ясувати, що їх немає; 2) зобразити схематично графік функції у=ах²+bx+c , звертаючи увагу тільки на точки перетину з віссю Ox і напрям віток параболи залежно від знака коефіцієнта а; 3) знайти на осі Ox проміжки, для яких виконується дана нерівність.

Приклад квадратної нерівності На ескізі графіка функції у=2х²-7х+6(див. рисунок) знайдемо проміжки, на яких у>0. Відповідь: (-∞;1,5)U(2;+∞).

Що таке квадратний тричлен? Квадратним тричленом називається многочлен виду ах²+bx+c , де x — змінна, a, b і c — деякі числа, причому а не дорівнює 0 . Коренем квадратного тричлена називається таке значення змінної, яке перетворює квадратний тричлен на 0. Щоб знайти корені квадратного тричлена, треба розв’язати квадратне рівняння ах²+bx+c=0. Теорема.Якщо х1 і х2- корені квадратного тричлена ах²+bx+c, то ах²+bx+c=а(х-х1)(х-х2) Приклад: 2х2+7х-4=0; а=2;b=7; с=-4; D=b2-4ac=49-4•2•-4=49+32=81=9; х1=0,5; х2=-4;

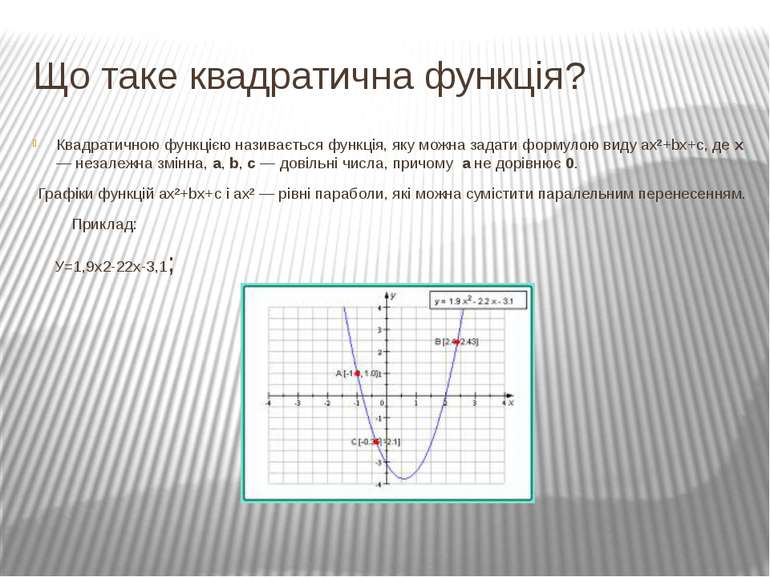
Що таке квадратична функція? Квадратичною функцією називається функція, яку можна задати формулою виду ах²+bx+c, де x — незалежна змінна, a, b, c — довільні числа, причому а не дорівнює 0. Графіки функцій ах²+bx+c і ах² — рівні параболи, які можна сумістити паралельним перенесенням. Приклад: У=1,9х2-22х-3,1;  

Схема побудови квадратичної функції При побудові параболи користуються такими загальними формулами та властивостями квадратичної функції. 1.Напрям віток параболи залежить від знака коефіцієнта a .а0 вітки параболи напрямлені вгору. 2. Точки перетину параболи з осями координат є такими: Абсциса точки перетину параболи з віссю Oy дорівнює 0, тоді ,у(0)=с,(0;с) . Ордината точок перетину параболи з віссю Ox дорівнює 0, тоді, щоб знайти абсциси цих точок, треба розв’язати квадратне рівняння ах²+bx+c=0. 3.Координати вершини параболи у=ах²+bx+c; Аналізуємо: 1.)D(y); хєR(-∞;+∞) 2.)Е(у); ує [0;+∞) а>0 ує(-∞;0] а

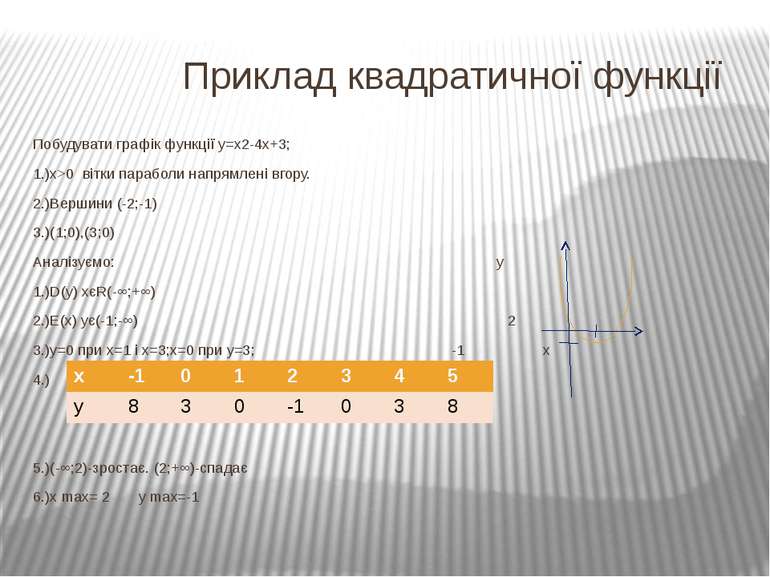
Приклад квадратичної функції Побудувати графік функції у=х2-4х+3; 1.)х>0 вітки параболи напрямлені вгору. 2.)Вершини (-2;-1) 3.)(1;0),(3;0) Аналізуємо: у 1.)D(y) хєR(-∞;+∞) 2.)Е(х) ує(-1;-∞) 2 3.)у=0 при х=1 і х=3;х=0 при у=3; -1 х 4.) 5.)(-∞;2)-зростає. (2;+∞)-спадає 6.)х max= 2 y max=-1 х -1 0 1 2 3 4 5 у 8 3 0 -1 0 3 8

Метод інтервалів Розв`яжемо нерівність (х+3)(х+2)(х-6)

Рівняння, що зводяться до квадратних Рівняння виду ах4+bx2+с=0,де а не дорівнює 0, називається біквадратним. Для його розв’язання вводять нову змінну: х2=у, у≥0.Приклад: 4х4-25х2+144=0;Нехай х2=у, у≥0; у2-25у+144=0;Розв’язавши це квадратне рівняння, знайдемо: у1=9; у=16; у=9; у=16; х2=9; х2=16; х1=3, х2=-3, х3=4, х4=-4; Відповідь: х1=3, х2=-3, х3=4, х4=-4;

Розв’язування систем рівнянь Розглянемо системи рівнянь, в яких одне або обидва рівняння другого степеня. Щоб розв’язати систему рівнянь графічним способом, треба побудувати в одній системі координат графіки обох рівнянь системи й знайти координати точок перетину графіків. Ці точки і будуть розв’язками системи рівнянь. Наприклад: Графіком першого рівняння є коло з центром в точці О(0;0) і радіусом 5 одиничних відрізків. Графік другого рівняння — парабола, вітки якої напрямлені вниз. Точки перетину з осями координат: (0; 5); Система має чотири розв’язки: Перевірка показує, що третій і четвертий розв’язки точні, а не наближені.