Презентація на тему:
Нерівності

Тема 2 Розв’язування лінійних нерівностей і систем нерівностей з однією змінною Лінійна нерівність з однією змінною. Рівносильні нерівності Система (та сукупність) нерівностей з однією змінною Числові проміжки. Переріз і об'єднання проміжків Нерівності, що містять модуль Розв’язування вправ. Самостійна робота Розв’язування систем ( та сукупностей) лінійних нерівностей з однією змінною. Доведення нерівностей Розв’язування вправ. Самостійна робота Розв'язування вправ

Пригадайте Чому дорівнює модуль додатного числа? Чому дорівнює модуль від'ємного числа? Чому дорівнює модуль нуля? Чому дорівнює модуль числа, яке позначене на координатній прямій?

Пункт 2.3. Нерівність Нерівність Приклади Нерівності, що містять модуль

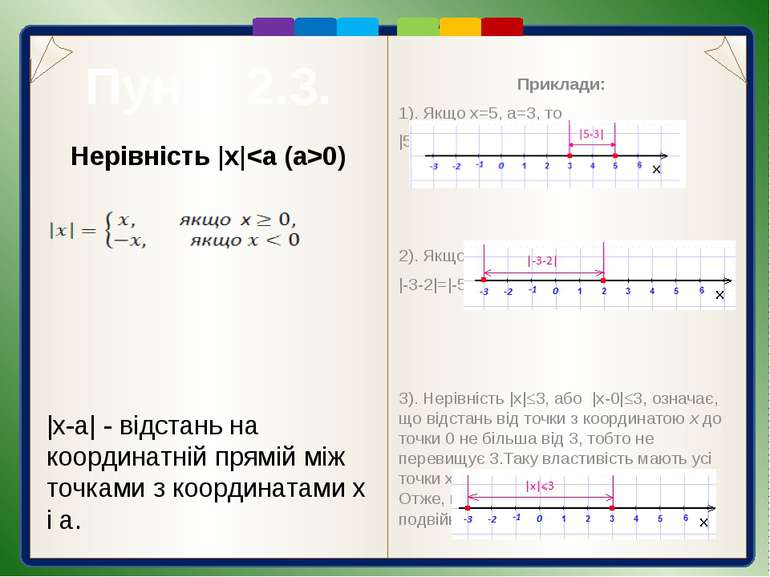
Пункт 2.3. Приклади: 1). Якщо х=5, а=3, то |5-3|=2 – відстань між точками 5 і 3 2). Якщо х=-3, а=2, то |-3-2|=|-5|=5 – відстань між точками -3 і 2 3). Нерівність |х|≤3, або |х-0|≤3, означає, що відстань від точки з координатою х до точки 0 не більша від 3, тобто не перевищує 3.Таку властивість мають усі точки х, що належать проміжку [-3; 3]. Отже, нерівність |х|≤3 рівносильна подвійній нерівності -3≤x≤3. Нерівність |x|0) |x-a| - відстань на координатній прямій між точками з координатами x і a.

2). Нерівність виду |x|0) рівносильна подвійній нерівності -а

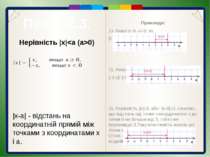
Пункт 2.3. Дану умову задовольняють точки, що розміщені на координатній прямій праворуч від точки з координатою а (x>a) і ліворуч від точки з координатою –а (xa (a>0) рівносильна сукупності двох нерівностей: x>a і xa (a>0), тобто |x-0|>a, означає, що відстань від точки з координатою х до точки 0 на координатній прямій більша від а.

Пункт 2.3. Розв'язання |x-1|≤3 -3≤x-1≤3, -3≤x≤4. Геометрична ілюстрація Відстань від точки з координатою 1 добудь-якої точки цього проміжку не перевищує 3. Відповідь. х [-2; 4]. Окремі приклади Приклад 1. Розв'язати нерівність |x-1|≤3

Пункт 2.3. Розв'язання |x-2|>3 x-2>3 і x-23+2 і x5 і x5) і зліва від точки з координатою -1 (x

Пункт 2.3. Розв'язання |2x-3|

Пункт 2.3. Розв'язання |x-1|+2х

1). Якій нерівності рівносильна нерівність |x|≤6? 2). Об'єднання розв'язків яких нерівностей є розв'язок нерівності |x|>10? Закріплення вивченого матеріалу

Пункт 2.3. Розв'язання |2x-3|<5 -5<2x-3<5, -5+3<2x-3+3<5+3, -2<2x<8, -1<x<4. Геометрична ілюстрація Відстань від точки з координатою 1,5 до будь-якої точки цього проміжку буде меншою від 2,5, бо нерівність -5<2x-3<5 (після ділення на 2) рівносильна нерівності -2,5<x-1,5>2,5. Відповідь. х (-1; 4).

Пункт 2.3. Розв'язання |x-1|+2х<5. За означенням модуля числа, Тому дана нерівність рівносильна сукупності двох систем нерівностей: і Розв'яжемо кожну з них. Відповідь. х (-∞; 2).

Закріплення вивченого матеріалу 1). Якій нерівності рівносильна нерівність |x|≤6? 2). Об'єднання розв'язків яких нерівностей є розв'язок нерівності |x|>10?