Презентація на тему:
Зьясування функції

Применение производной к исследованию функции Цель урока: научиться исследовать функцию и строить её график с использованием производной

Ответь на вопросы: Повторим

Что называется функцией? Вопрос №1

Если каждому значению переменной Х из некоторого множества D соответствует единственное значение переменной У, то такое соответствие называется функцией. При этом Х называют независимой переменной, или аргументом, а У -зависимой переменой, или функцией.

Что называется областью определения и областью значения функции? Вопрос№2

Множество всех значений, которые может принимать аргумент, называют областью определения данной функции и обозначают D. Множество значений, которые может принимать функция, называют областью значений и обозначают буквой Е.

Какая функция называется чётной (нечётной)? Вопрос №3

Функция называется чётной (нечётной), если область её определения симметрична относительно числа 0 и для каждого значения Х из области определения f(-x)=f(x), (f(-x)=-f(x) )

Какие точки называются критическими? Вопрос №4

Внутренние точки области определения, в которых производная равна нулю или не существует, называют – критическими точками функции.

Дать определение, на каком промежутке функция возрастает, убывает, постоянная Вопрос №5

Если производная функции в каждой точке некоторого промежутка положительная, то функция на этом промежутке возрастает. Если производная функции в каждой точке некоторого промежутка отрицательная, то функция на этом промежутке убывает. Если производная функции в каждой точке промежутка тождественно равна нулю, то на этом промежутке функция постоянная.

Как можно определить промежутки возрастания и убывания функции f(x)? Вопрос №6

ӏ способ: нужно решить неравенства f᾽(x)>0 и f᾽(x)

Что называется точкой минимума (максимума) функции? Вопрос №7

Точка х0 называется точкой минимума функции f(x), если для всех х (х≠х0) из некоторой окрестности точки х0 выполняется неравенство f(x0)f(x))

Как, одним словом назвать точки максимума и минимума функции? Вопрос №8

Точки экстремума

Как определить точки экстремума? Вопрос №9

Точка х0, при переходе через которую в направлении роста аргумента производная меняет знак с «+» на «-» является точкой максимума, а точка при переходе через которую производная меняет знак с «-» ни «+»-точкой минимума

По графику функции определить её свойства

Записать в тетрадь!

Найти область определения функции Исследовать функцию на чётность, нечётность и периодичность Найти нули функции (точки пересечения графика функции с осями координат) Исследовать функцию на монотонность (найти промежутки возрастания и убывания функции) Найти точки экстремума и экстремальные значения функции Найти дополнительные точки (если нужно) Построить график функции Схема исследования функции

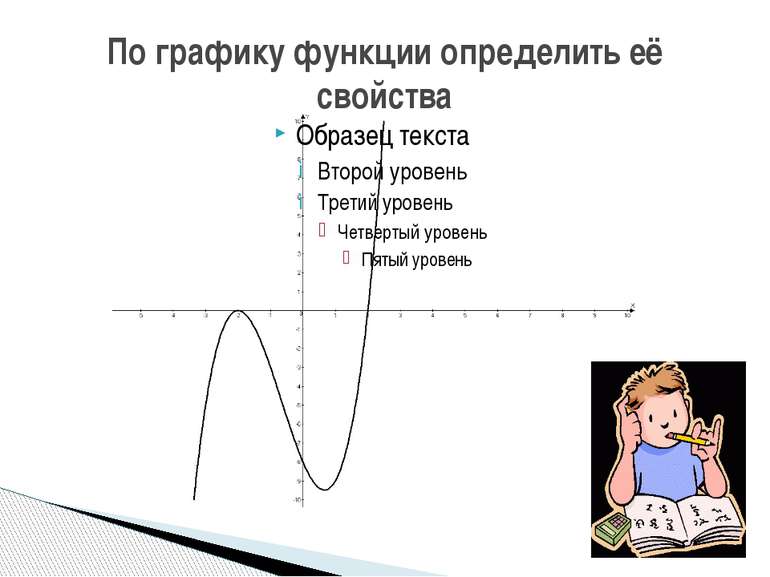
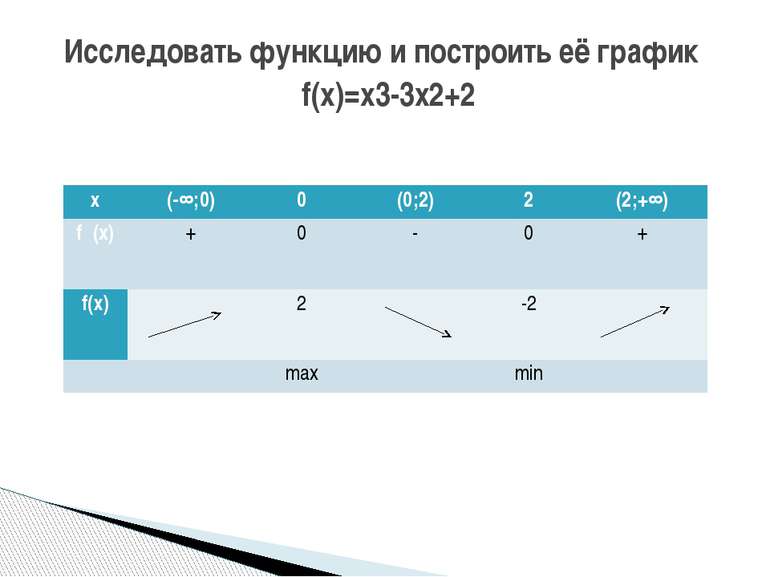
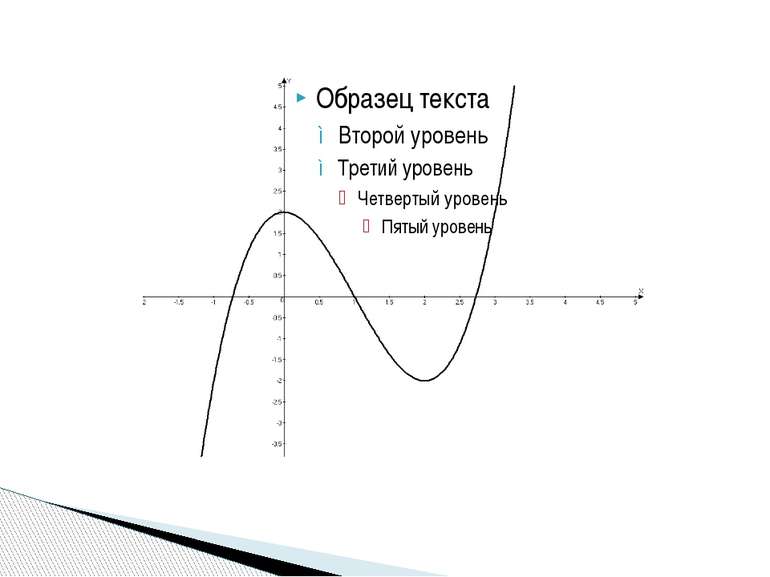
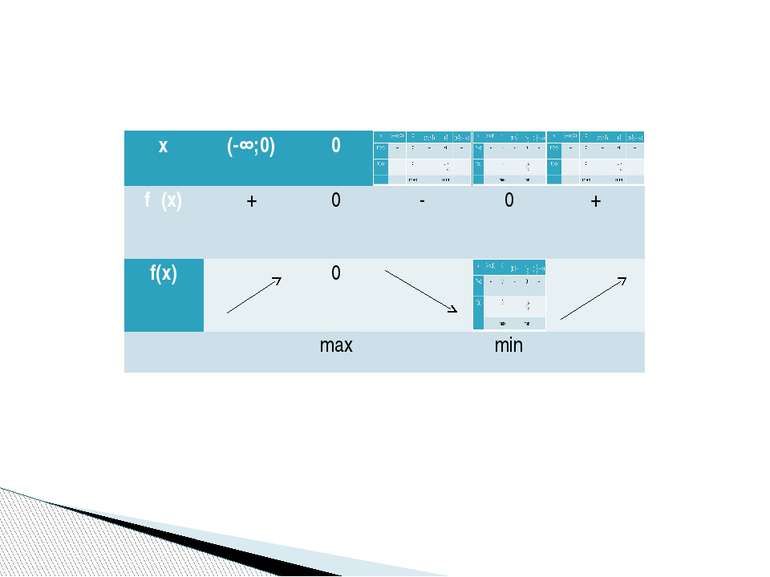
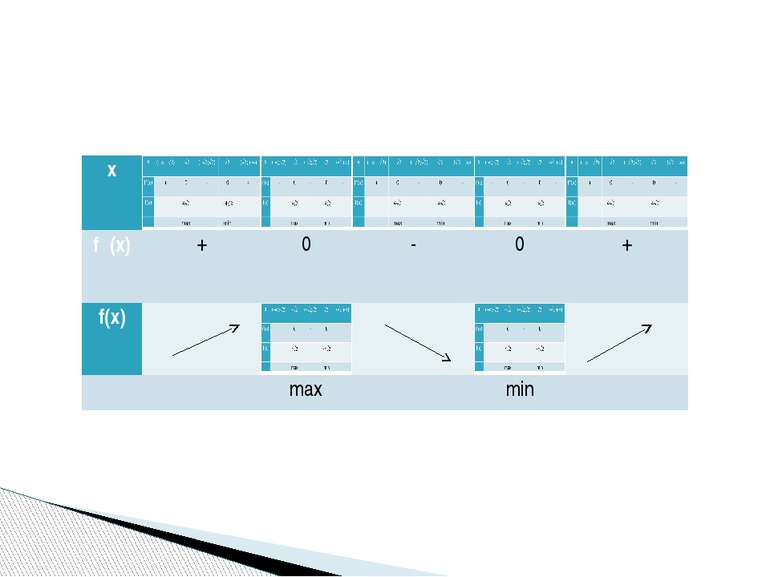
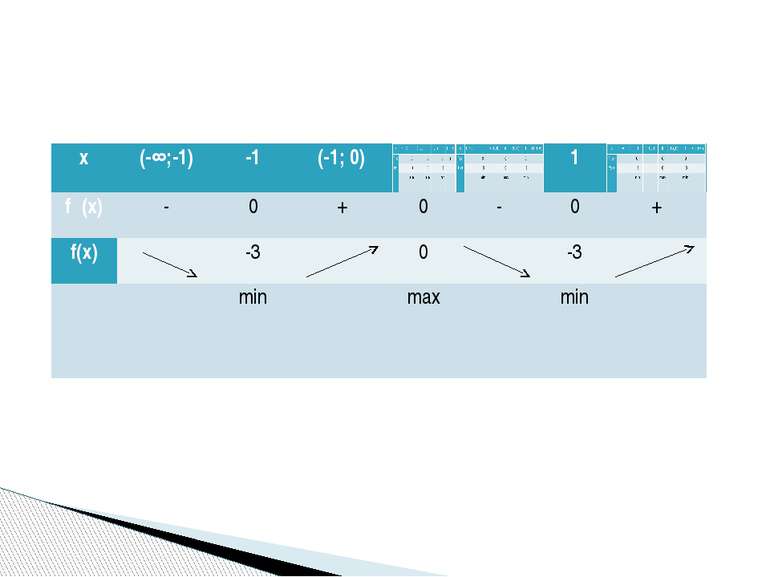
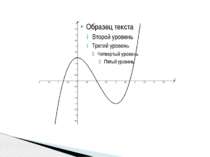
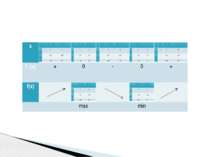
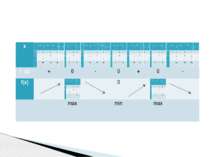
Исследовать функцию и построить её график f(x)=x3-3x2+2 х (-∞;0) 0 (0;2) 2 (2;+∞) f᾽(x) + 0 - 0 + f(х) 2 -2     max   min  

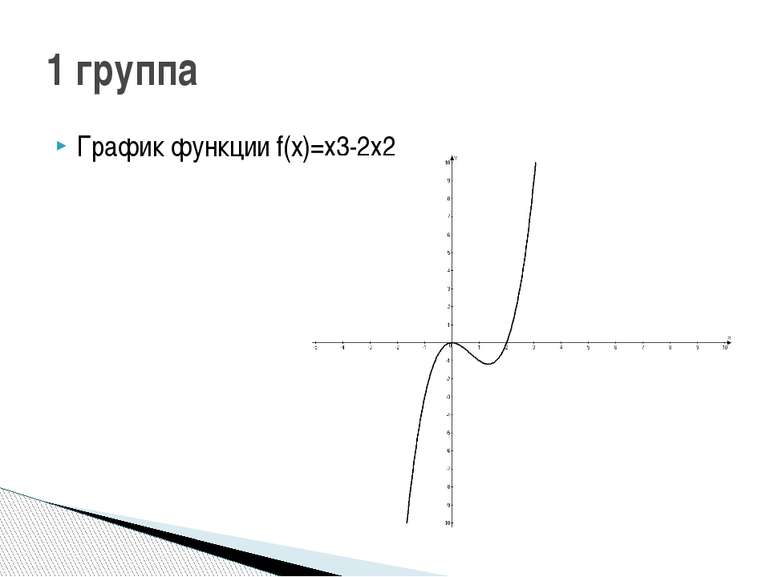
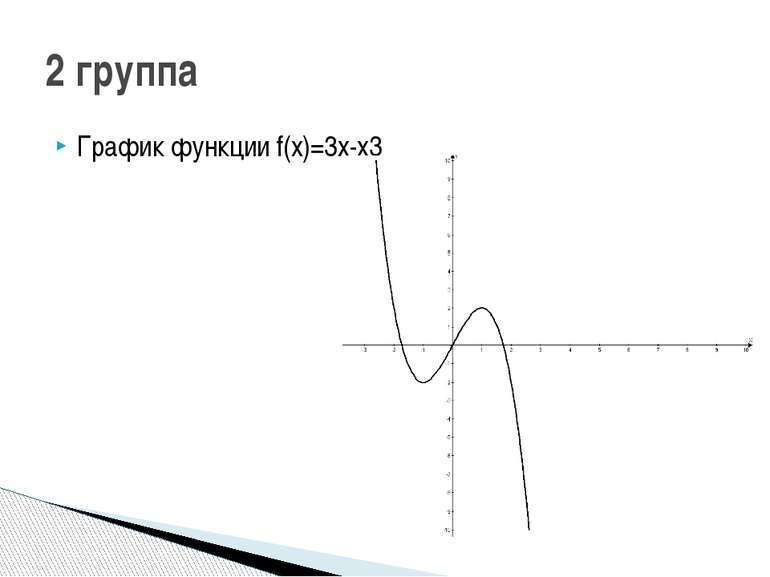
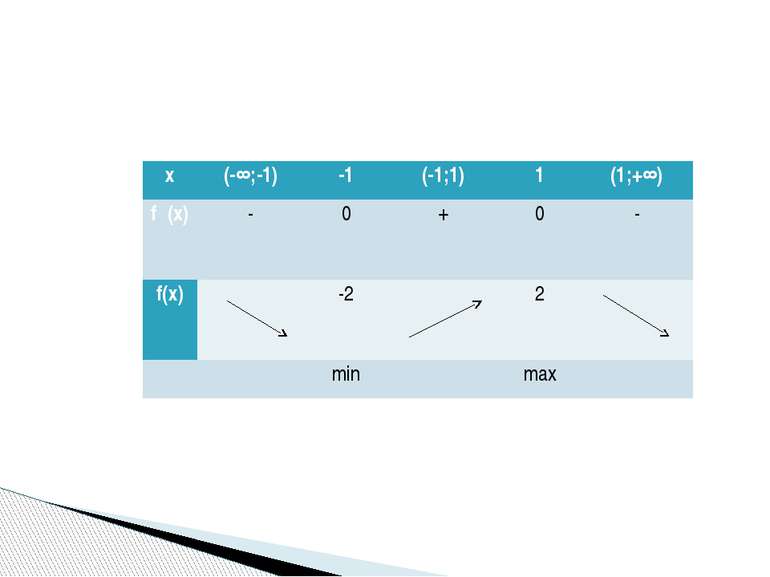
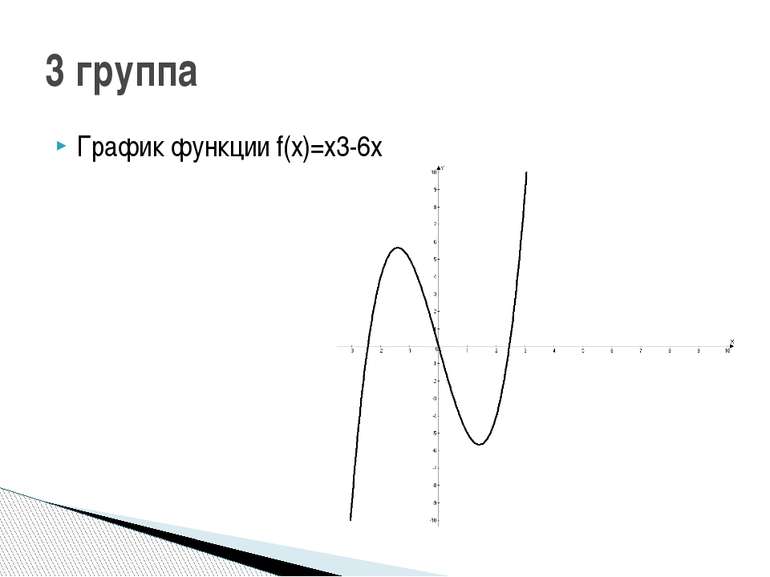
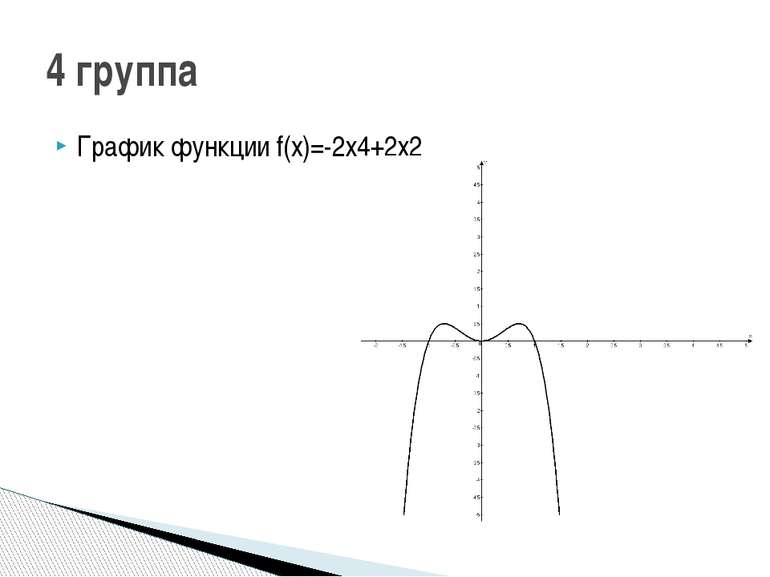
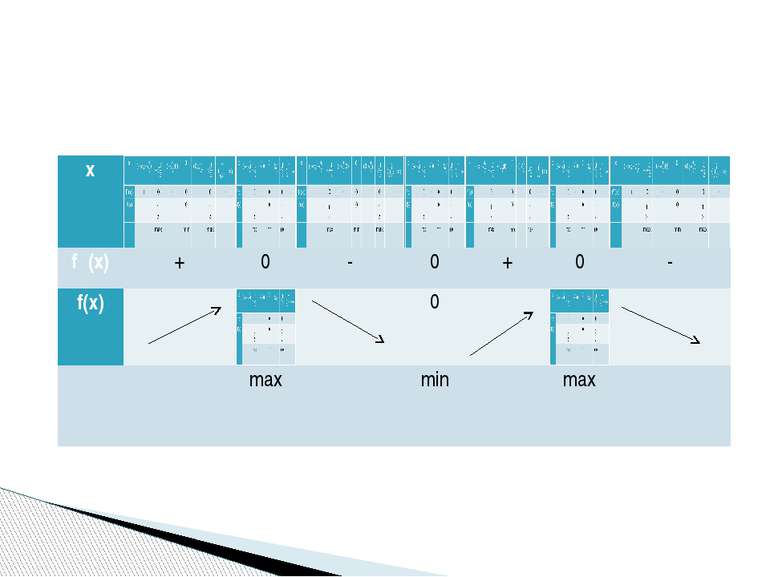
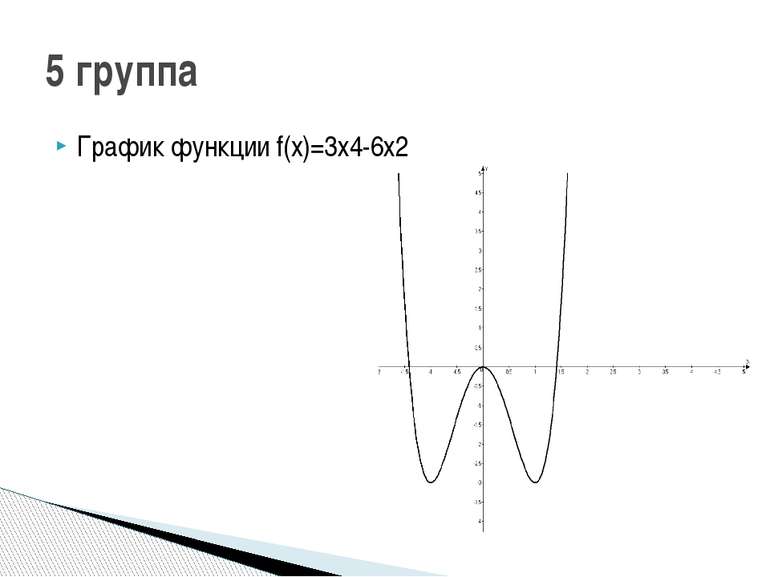
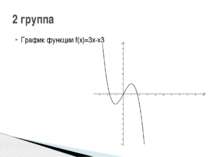
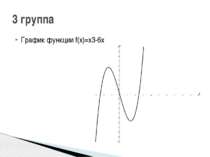
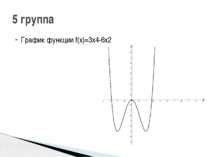
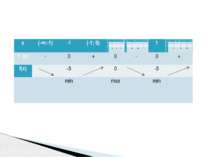
1 группа: f(x)=x3-2х2 2 группа: f(x)=3x-x3 3 группа: f(x)=x3-6x 4 группа: f(x)=-2х4+2х2 5 группа: f(x)=3х4-6х2 Исследуйте функцию и постройте её график

График функции f(x)=x3-2х2 1 группа

График функции f(x)=3x-x3 2 группа

х (-∞;-1) -1 (-1;1) 1 (1;+∞) f᾽(x) - 0 + 0 - f(х) -2 2     min   max  

График функции f(x)=x3-6x 3 группа

График функции f(x)=-2х4+2х2 4 группа

График функции f(x)=3х4-6х2 5 группа

Спасибо за урок!