Презентація на тему:
Спецкурс «Microsoft Excel у профільному навчанні»

Розділ 10 Статистичні методи вивчення взаємозв'язку даних Спецкурс «Microsoft Excel у профільному навчанні»

План вивчення теми У цьому розділі буде розглянуто: статистичні ряди розподілу; поняття кореляційного зв'язку та коефіцієнта кореляції; кореляційну матрицю; рівняння та лінії тренду; прогнозування даних.

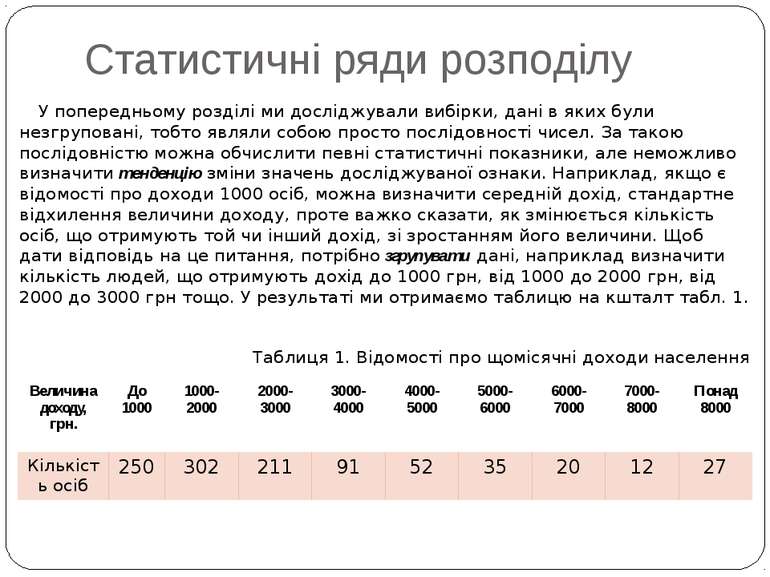
Статистичні ряди розподілу У попередньому розділі ми досліджували вибірки, дані в яких були незгруповані, тобто являли собою просто послідовності чисел. За такою послідовністю можна обчислити певні статистичні показники, але неможливо визначити тенденцію зміни значень досліджуваної ознаки. Наприклад, якщо є відомості про доходи 1000 осіб, можна визначити середній дохід, стандартне відхилення величини доходу, проте важко сказати, як змінюється кількість осіб, що отримують той чи інший дохід, зі зростанням його величини. Щоб дати відповідь на це питання, потрібно згрупувати дані, наприклад визначити кількість людей, що отримують дохід до 1000 грн, від 1000 до 2000 грн, від 2000 до 3000 грн тощо. У результаті ми отримаємо таблицю на кшталт табл. 1. Таблиця 1. Відомості про щомісячні доходи населення Величина доходу,грн. До 1000 1000-2000 2000-3000 3000-4000 4000-5000 5000-6000 6000-7000 7000-8000 Понад 8000 Кількість осіб 250 302 211 91 52 35 20 12 27

Статистичні ряди розподілу Побудована таблиця називається статистичним рядом розподілу. Загалом ряд розподілу — це два набори значень однакової довжини. В одному наборі представлені значення певної ознаки (у табл. 1 це величина доходу), а в іншому — частоти, тобто кількості разів, коли під час статистичного спостереження було отримано відповідне значення ознаки. Інакше кажучи, ідеться про розподіл певних об'єктів за певною ознакою. Наприклад, у табл.1 наведено розподіл осіб за величиною доходу. Величина доходу — це ознака, а кількості осіб — частоти. За рядом розподілу вже можна визначити тенденцію зміни значень досліджуваної ознаки. Так, з табл. 1 видно, що з ростом доходу від 0 до 2000 грн. кількість осіб, які отримують цей дохід, зростає, а коли дохід перевищує 2000 грн., тенденція зворотна: що вище дохід, то менша кількість людей його отримує. Таблиця 1. Відомості про щомісячні доходи населення Величина доходу,грн. До 1000 1000-2000 2000-3000 3000-4000 4000-5000 5000-6000 6000-7000 7000-8000 Понад 8000 Кількість осіб 250 302 211 91 52 35 20 12 27

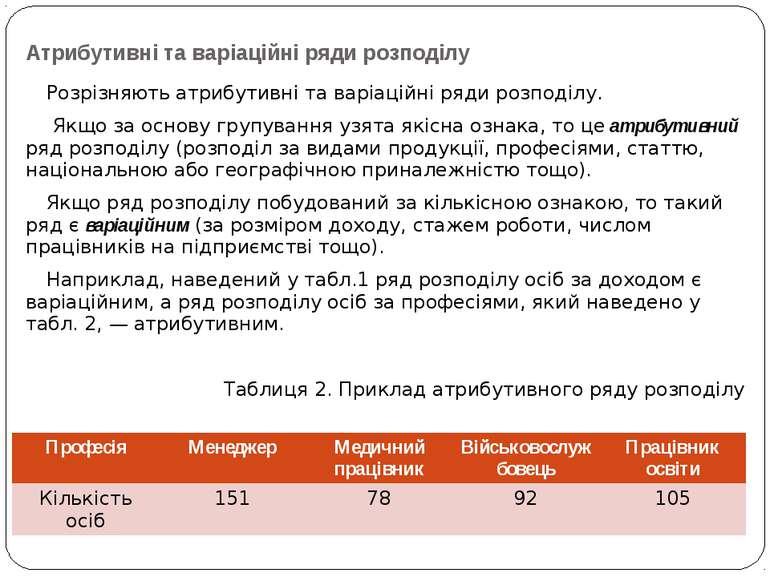
Атрибутивні та варіаційні ряди розподілу Розрізняють атрибутивні та варіаційні ряди розподілу. Якщо за основу групування узята якісна ознака, то це атрибутивний ряд розподілу (розподіл за видами продукції, професіями, статтю, національною або географічною приналежністю тощо). Якщо ряд розподілу побудований за кількісною ознакою, то такий ряд є варіаційним (за розміром доходу, стажем роботи, числом працівників на підприємстві тощо). Наприклад, наведений у табл.1 ряд розподілу осіб за доходом є варіаційним, а ряд розподілу осіб за професіями, який наведено у табл. 2, — атрибутивним. Таблиця 2. Приклад атрибутивного ряду розподілу Професія Менеджер Медичний працівник Військовослужбовець Працівник освіти Кількість осіб 151 78 92 105

Дискретні та інтервальні ряди розподілу Варіаційні ряди розподілу, у свою чергу, поділяються на дискретні та інтервальні. У дискретному ряді розподілу частоти зіставляються окремим значенням ознаки, а в інтервальному — інтервалам таких значень. Так, ряд розподілу у табл. 1 є інтервальним. У табл. 3 наведено приклад дискретного ряду розподілу — це розподіл кількостей випадання чисел на гральній кістці. Значення ознаки у дискретному ряді називають варіантами. Таблиця 3. Приклад дискретного ряду розподілу Число на гральній кістці 1 2 3 4 5 6 Кількість випадань 50 43 51 47 39 53

Дискретні та інтервальні ряди розподілу Інтервальний ряд розподілу можна перетворити на дискретний, взявши за значення варіант середини інтервалів. Так, у табл.4 наведено дискретний ряд, який побудовано за інтервальним рядом, поданим у табл. 1. Зверніть увагу: хоча останній інтервал мав вигляд [8000; ), за його середину ми взяли число 8500, припустивши, що відстань між двома останніми значеннями ознаки дорівнює відстані між передостанніми значеннями: 7500 - 6500 = 1000; 7500 + 1000 = 8500. Таблиця 4. Дискретний ряд розподілу осіб за доходами Очевидно, що атрибутивні ряди розподілу можуть бути тільки дискретними. Величина доходу,грн. 500 1500 2500 3500 4500 5500 6500 7500 8500 Кількість осіб 250 302 211 91 52 35 20 12 27

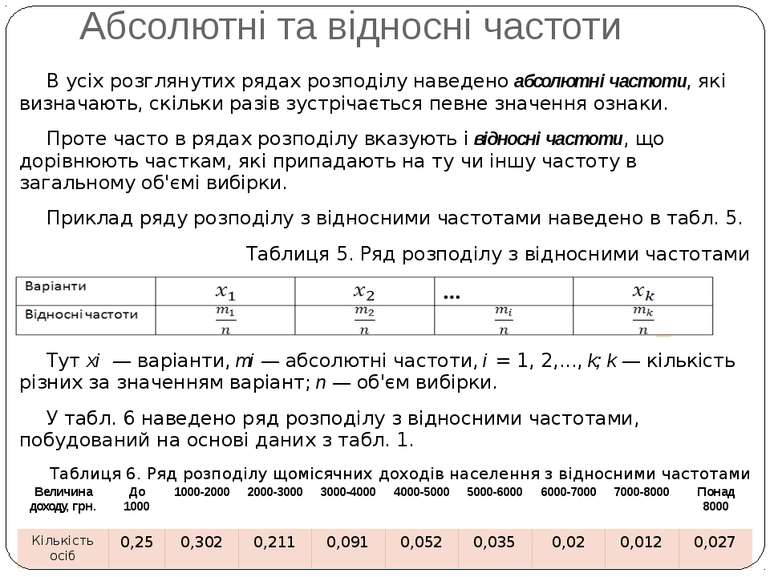
Абсолютні та відносні частоти В усіх розглянутих рядах розподілу наведено абсолютні частоти, які визначають, скільки разів зустрічається певне значення ознаки. Проте часто в рядах розподілу вказують і відносні частоти, що дорівнюють часткам, які припадають на ту чи іншу частоту в загальному об'ємі вибірки. Приклад ряду розподілу з відносними частотами наведено в табл. 5. Таблиця 5. Ряд розподілу з відносними частотами Тут хі — варіанти, ті — абсолютні частоти, і = 1, 2,..., k; k — кількість різних за значенням варіант; п — об'єм вибірки. У табл. 6 наведено ряд розподілу з відносними частотами, побудований на основі даних з табл. 1. Таблиця 6. Ряд розподілу щомісячних доходів населення з відносними частотами Величина доходу,грн. До 1000 1000-2000 2000-3000 3000-4000 4000-5000 5000-6000 6000-7000 7000-8000 Понад 8000 Кількість осіб 0,25 0,302 0,211 0,091 0,052 0,035 0,02 0,012 0,027

Побудова рядів розподілу Припустимо, що результати статистичних спостережень необхідно згрупувати, побудувавши ряд розподілу. Ця операція виконується у кілька етапів. Насамперед необхідно визначити, який ряд розподілу будувати — інтервальний чи дискретний. Критерій такий: якщо ознака може набувати лише невелику кількість різних значень (у межах одного-двох десятків), будуйте дискретний ряд розподілу, інакше — інтервальний. Не плутайте випадок, коли ознака представлена у вибірці невеликою кількістю значень, з випадком, коли вона може набувати невеликої кількості значень у генеральній сукупності. Наприклад, якщо є вибірка з відомостями про зріст семи людей, то це ще не означає, що величина «зріст» може мати лише сім значень. А якщо є вибірка днів тижня, то величина «день тижня» дійсно може набувати лише семи різних значень. Для побудови дискретного ряду розподілу слід виписати всі можливі значення ознаки, а потім підрахувати, скільки разів кожне з них трапляється у вибірці — це будуть частоти. У Microsoft Excel для підрахунку частот слід застосувати функцію COUNTIF (рос. СЧЕТЕСЛИ).

Побудова рядів розподілу Для побудови за вибіркою хi , ..., хп ряду розподілу, що складається з m рівних інтервалів, необхідно виконати такі кроки. 1. Визначити найбільшу та найменшу варіанти — хтіп та хтах 2. Визначити величину інтервалу 3. Визначити межі інтервалів за формулами: Тобто нижня межа першого інтервалу дорівнює найменшій варіанті, а кожна наступна межа більша за попередню на h.

Побудова рядів розподілу 4. Підрахувати, скільки варіант потрапляє у кожен інтервал — це і будуть частоти. В Excel це можна зробити за допомогою функції FREQUENCY (рос. ЧАСТОТА), яка має два аргументи: FREQUENCY (діапазон_вибірки;діапазон_меж_інтервалів). Перший аргумент — це діапазон, що містить вибірку, а другий — діапазон усіх меж інтервалів, за винятком у0 та ут (тобто усіх меж між інтервалами). Результатом функції буде набір частот, що відповідають кожному інтервалу. Ви вперше стикаєтеся з функцією, результатом якої є діапазон значень, а не окреме значення. Її і вводити потрібно дещо інакше, ніж інші функції. А саме, слід виділити весь діапазон, де міститимуться результати, ввести формулу функції та натиснути клавіші Ctrl+Shift+Enter.  

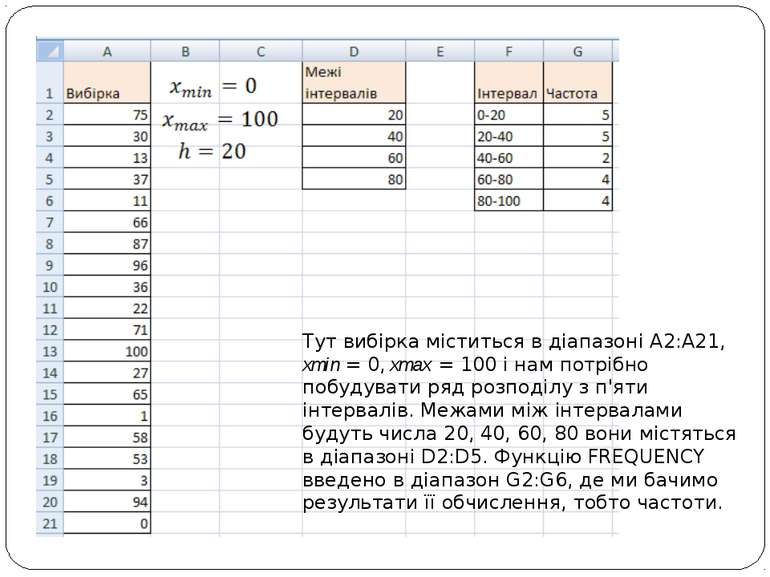
Тут вибірка міститься в діапазоні А2:А21, хmin = 0, хтах = 100 і нам потрібно побудувати ряд розподілу з п'яти інтервалів. Межами між інтервалами будуть числа 20, 40, 60, 80 вони містяться в діапазоні D2:D5. Функцію FREQUENCY введено в діапазон G2:G6, де ми бачимо результати її обчислення, тобто частоти.

Побудова рядів розподілу   Процес введення функції FREQUENCY зображено на рис.

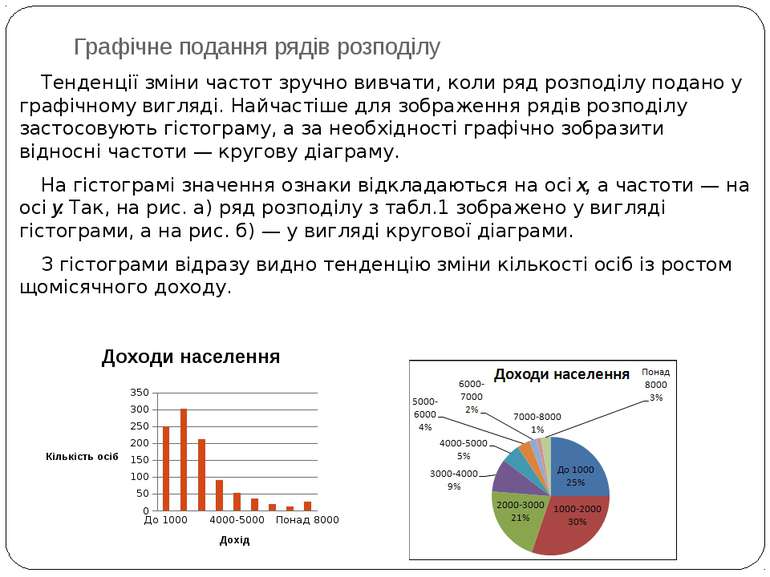
Графічне подання рядів розподілу Тенденції зміни частот зручно вивчати, коли ряд розподілу подано у графічному вигляді. Найчастіше для зображення рядів розподілу застосовують гістограму, а за необхідності графічно зобразити відносні частоти — кругову діаграму. На гістограмі значення ознаки відкладаються на осі х, а частоти — на осі у. Так, на рис. а) ряд розподілу з табл.1 зображено у вигляді гістограми, а на рис. б) — у вигляді кругової діаграми. З гістограми відразу видно тенденцію зміни кількості осіб із ростом щомісячного доходу.

Вправа 10.1. Побудова інтервального ряду розподілу У файлі наведено відомості про зріст учнів класу. Потрібно побудувати ряд розподілу учнів за зростом з п'ятьма рівними інтервалами, зобразити його графічно та зробити висновок щодо характеру зв'язку між зростом та кількістю учнів цього зросту.

Обчислення статистичних показників варіаційних рядів розподілу Якщо вибірку подано у вигляді варіаційного ряду розподілу, а не як набір варіант, то формули для обчислення середнього та стандартного відхилення будуть дещо складніші. Отже, припустимо, що є такий ряд розподілу, як показано в табл. 7. Середнє значення вибірки обчислюється за формулою середньої арифметичної зваженої: (1) Тут кожне значення варіанти «зважується», тобто множиться на відповідну їй частоту. Дисперсію варіаційного ряду найлегше обчислити за такою формулою: (2) Ну а стандартне відхилення — це корінь із дисперсії: (3) Варіанти х1 х2 … хk Частоти n1 n2 … nk

Обчислення статистичних показників варіаційних рядів розподілу У Microsoft Excel спеціальних функцій для обчислення статистичних показників за формулами (1)-(3) не передбачено. Тому визначати ці величини потрібно, обчислюючи кожну суму за допомогою функції SUM (рос. СУММ) з подальшим застосуванням необхідних арифметичних перетворень. За потреби обчислити статистичні показники для інтервального ряду розподілу його спочатку слід перетворити на дискретний, як це описано в підрозділі «Дискретні та інтервальні ряди розподілу».

Вправа 10.2. Обчислення статистичних показників У файлі показано ряд розподілу підприємств міста N за прибутком. Обчисліть середній прибуток та стандартне відхилення прибутку цих підприємств. Зробіть висновки.

Основи кореляційного та регресійного аналізу У ряді розподілу зіставляються дві послідовності значень: певної ознаки та частот. Залежність між цими послідовностями простежується не завжди. Побудова ряду розподілу дає змогу зробити лише приблизні, «інтуїтивні» висновки щодо того, чи існує залежність між значеннями ознаки та частотами і який вона має характер. Крім того, залежності можуть існувати між довільними вибірками, а не лише між ознакою та частотами. Більш точне дослідження залежностей між двома чи більшою кількістю вибірок є завданням спеціальних розділів математичної статистики — кореляційного та регресійного аналізу. Кореляційний аналіз дає змогу встановити, чи існує зв'язок між явищами і наскільки цей зв'язок сильний (часто його називають кореляційним зв'язком). Якщо зв'язок виявився суттєвим, то доцільно скористатися методами регресійного аналізу, основне завдання якого полягає у визначенні характеру зв'язку і побудові його математичної моделі. На основі моделі можна передбачити ту або іншу подію, спрогнозувати, як будуть розвиватися певні процеси у разі змінення характеристик об'єкта дослідження.

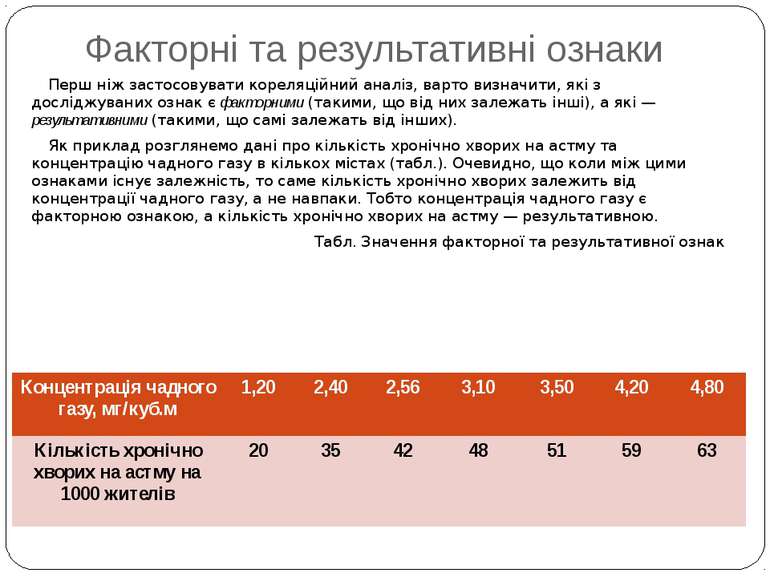
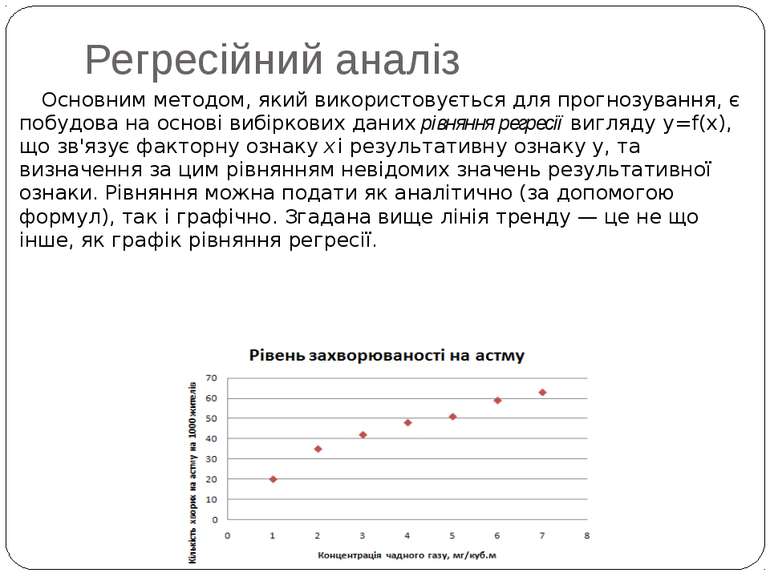
Факторні та результативні ознаки Перш ніж застосовувати кореляційний аналіз, варто визначити, які з досліджуваних ознак є факторними (такими, що від них залежать інші), а які — результативними (такими, що самі залежать від інших). Як приклад розглянемо дані про кількість хронічно хворих на астму та концентрацію чадного газу в кількох містах (табл.). Очевидно, що коли між цими ознаками існує залежність, то саме кількість хронічно хворих залежить від концентрації чадного газу, а не навпаки. Тобто концентрація чадного газу є факторною ознакою, а кількість хронічно хворих на астму — результативною. Табл. Значення факторної та результативної ознак Концентрація чадного газу, мг/куб.м 1,20 2,40 2,56 3,10 3,50 4,20 4,80 Кількість хронічно хворих на астму на 1000 жителів 20 35 42 48 51 59 63

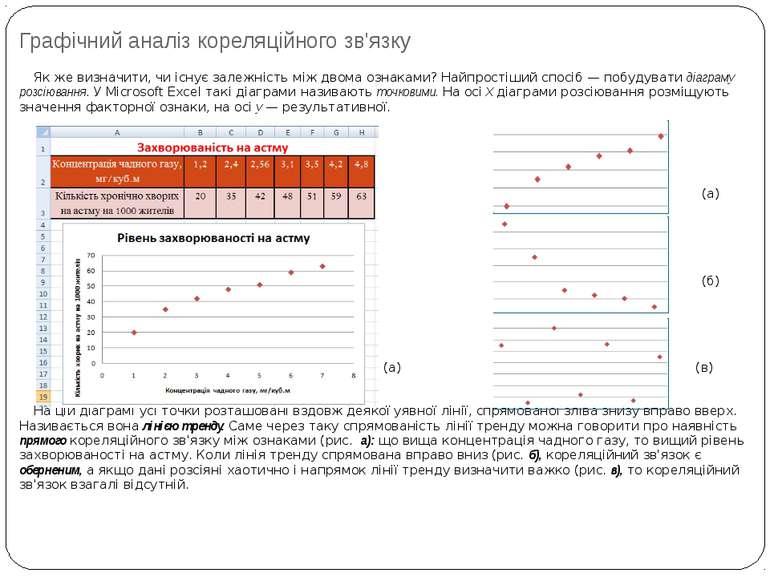
Графічний аналіз кореляційного зв'язку Як же визначити, чи існує залежність між двома ознаками? Найпростіший спосіб — побудувати діаграму розсіювання. У Microsoft Excel такі діаграми називають точковими. На осі X діаграми розсіювання розміщують значення факторної ознаки, на осі у — результативної. (а) (б)   (а) (в) На цій діаграмі усі точки розташовані вздовж деякої уявної лінії, спрямованої зліва знизу вправо вверх. Називається вона лінією тренду. Саме через таку спрямованість лінії тренду можна говорити про наявність прямого кореляційного зв'язку між ознаками (рис. а): що вища концентрація чадного газу, то вищий рівень захворюваності на астму. Коли лінія тренду спрямована вправо вниз (рис. б), кореляційний зв'язок є оберненим, а якщо дані розсіяні хаотично і напрямок лінії тренду визначити важко (рис. в), то кореляційний зв'язок взагалі відсутній.

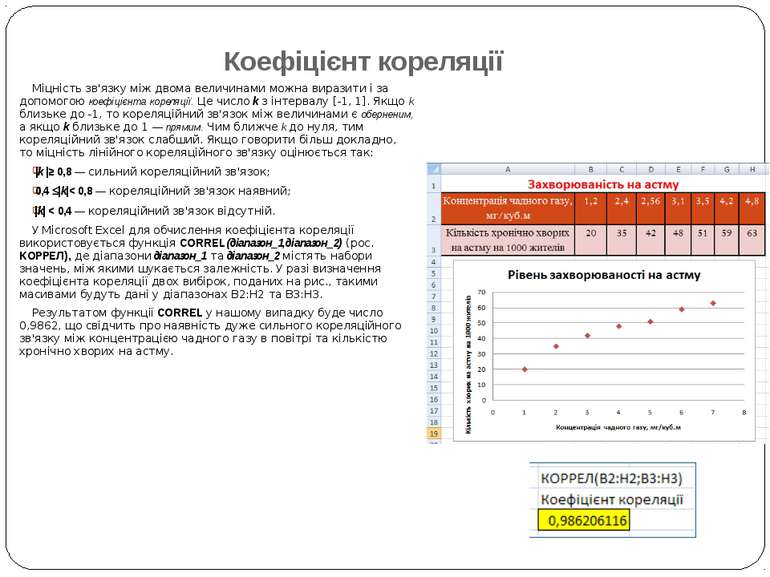
Коефіцієнт кореляції Міцність зв'язку між двома величинами можна виразити і за допомогою коефіцієнта кореляції. Це число k з інтервалу [-1, 1]. Якщо k близьке до -1, то кореляційний зв'язок між величинами є оберненим, а якщо k близьке до 1 — прямим. Чим ближче k до нуля, тим кореляційний зв'язок слабший. Якщо говорити більш докладно, то міцність лінійного кореляційного зв'язку оцінюється так: |k |≥ 0,8 — сильний кореляційний зв'язок; 0,4 |k|< 0,8 — кореляційний зв'язок наявний; |k| < 0,4 — кореляційний зв'язок відсутній. У Microsoft Excel для обчислення коефіцієнта кореляції використовується функція CORREL(діапазон_1,діапазон_2) (рос. КОРРЕЛ), де діапазони діапазон_1 та діапазон_2 містять набори значень, між якими шукається залежність. У разі визначення коефіцієнта кореляції двох вибірок, поданих на рис., такими масивами будуть дані у діапазонах В2:Н2 та ВЗ:НЗ. Результатом функції CORREL у нашому випадку буде число 0,9862, що свідчить про наявність дуже сильного кореляційного зв'язку між концентрацією чадного газу в повітрі та кількістю хронічно хворих на астму.

Коефіцієнт кореляції Зазначимо, що функція CORREL визначає коефіцієнт лінійної кореляції, яка свідчить про наявність саме лінійного зв'язку між ознаками. Цей зв'язок буде тим сильніший, чим ближче до певної прямої розташовані точки на діаграмі розсіювання. Насправді існують й інші типи зв'язків. Наприклад, той факт, що точки на діаграмі розсіювання розташовані близько до певної параболи, свідчить про наявність між ознаками квадратичного зв'язку; щоправда, коефіцієнт лінійної кореляції при цьому може бути незначним.

Кореляційна матриця Коли потрібно порівняти не два, а більше масивів експериментальних даних, будують кореляційну матрицю — таблицю, у якій коефіцієнти кореляції між ознаками розташовані на перетині відповідних рядків і стовпців. Для побудови кореляційної матриці використовують інструмент Кореляція, який запускається за допомогою команди Дані, Аналіз, Аналіз даних, Кореляція. Якщо меню Дані не містить команди Аналіз даних, необхідно виконати команду Офіс, Параметри Excel, Надбудови, Перейти, та встановити прапорець Пакет аналізу, Ок. У групі команд Аналіз додається команда Аналіз даних.

Регресійний аналіз Основне завдання регресійного аналізу — прогнозування. Щоб навести приклад задачі на прогнозування, повернімось до вибірок з табл. Значення факторної ознаки (концентрації чадного газу), отримані в результаті статистичного спостереження, коливаються в межах від 1,2 до 4,8 мг/м3. Для цих значень рівень захворюваності на астму відомий. Але задамося питанням: яким буде цей рівень, якщо концентрація чадного газу становитиме 10 мг/м3? Тобто спробуємо спрогнозувати значення результативної ознаки у разі виходу значення факторної ознаки за межі інтервалу вибірки. Концентрація чадного газу, мг/куб.м 1,20 2,40 2,56 3,10 3,50 4,20 4,80 Кількість хронічно хворих на астму на 1000 жителів 20 35 42 48 51 59 63

Регресійний аналіз Основним методом, який використовується для прогнозування, є побудова на основі вибіркових даних рівняння регресії вигляду y=f(x), що зв'язує факторну ознаку х і результативну ознаку у, та визначення за цим рівнянням невідомих значень результативної ознаки. Рівняння можна подати як аналітично (за допомогою формул), так і графічно. Згадана вище лінія тренду — це не що інше, як графік рівняння регресії.

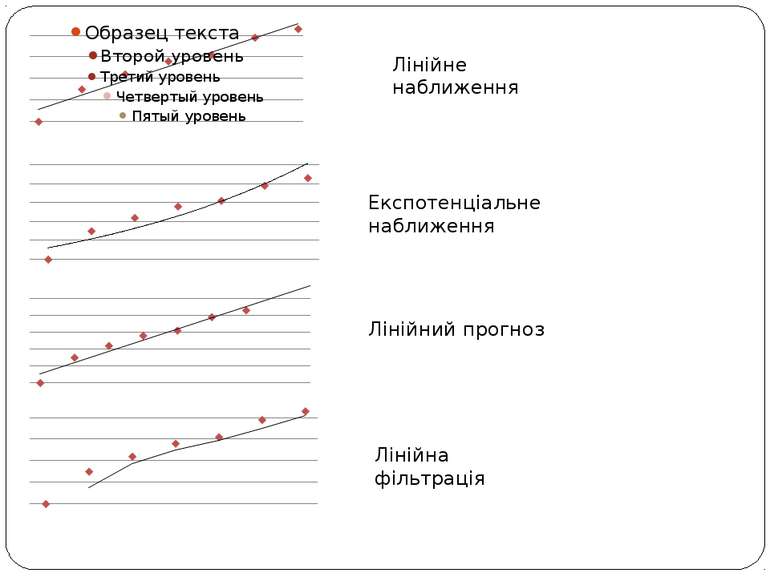
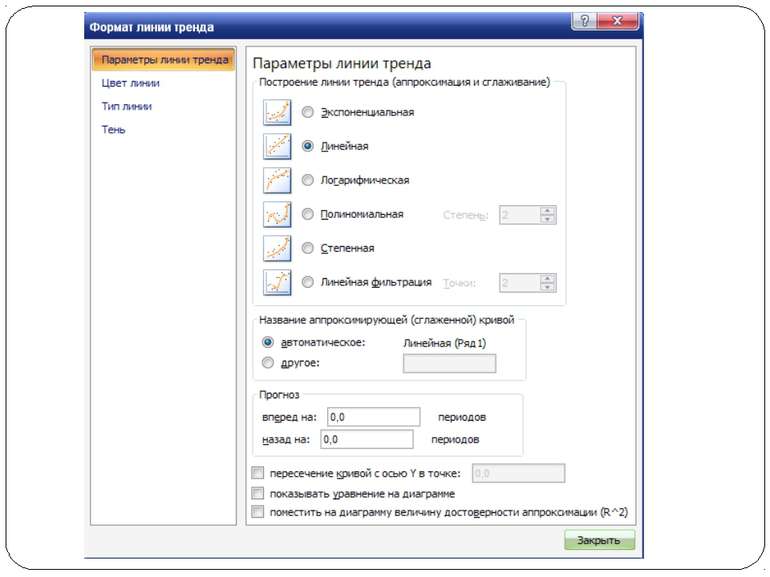
Регресійний аналіз У Microsoft Excel передбачена можливість автоматичної побудови лінії тренду. Для цього спочатку слід виділити діаграму розсіювання та виконати команду Діаграма, Лінія тренду, вказати тип. Або вибрати Додаткові параметри лінії тренда, та у вікні Формат лінії тренда вказати тип залежності між факторною та результативною ознаками — лінійна, поліноміальна (квадратична, кубічна тощо), логарифмічна та ін.

Лінійне наближення Експотенціальне наближення Лінійний прогноз Лінійна фільтрація

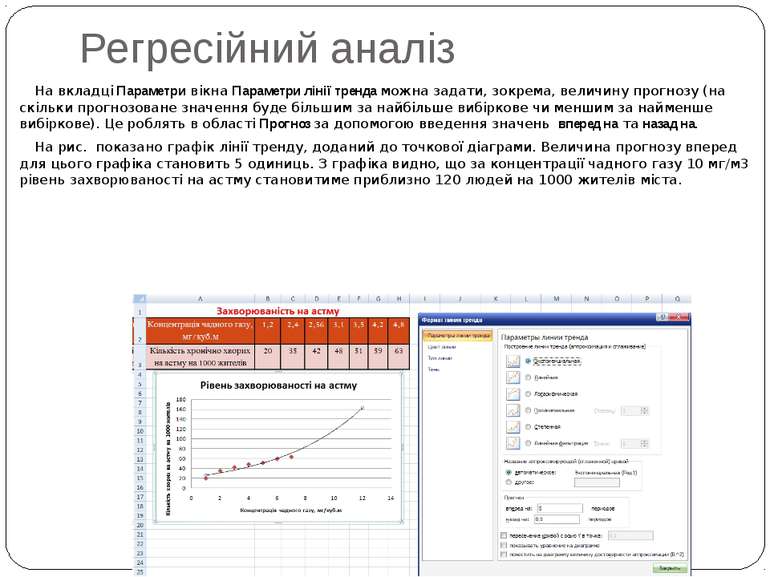
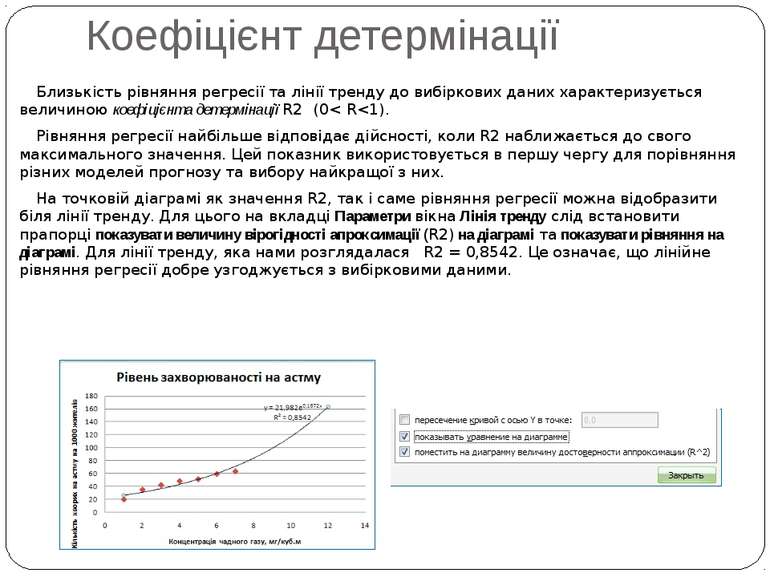
Регресійний аналіз На вкладці Параметри вікна Параметри лінії тренда можна задати, зокрема, величину прогнозу (на скільки прогнозоване значення буде більшим за найбільше вибіркове чи меншим за найменше вибіркове). Це роблять в області Прогноз за допомогою введення значень вперед на та назад на. На рис. показано графік лінії тренду, доданий до точкової діаграми. Величина прогнозу вперед для цього графіка становить 5 одиниць. З графіка видно, що за концентрації чадного газу 10 мг/м3 рівень захворюваності на астму становитиме приблизно 120 людей на 1000 жителів міста.

Коефіцієнт детермінації Близькість рівняння регресії та лінії тренду до вибіркових даних характеризується величиною коефіцієнта детермінації R2 (0< R

Вправа 10.3. Виявлення кореляційного зв'язку Протягом року продовольча компанія здійснювала рекламу своєї продукції шляхом виготовлення та розповсюдження рекламних листівок у кількості від 89 000 до 345 000 шт. за місяць. Потрібно визначити, чи був цей захід ефективним та як вплине на дохід компанії виготовлення та розповсюдження протягом місяця 500 000 листівок.