Презентація на тему:
Швидкість зростання функції. Асимптотичні позначення. Елементарні структури даних. Зв’язані списки

Алгоритми та структури даних Лекція 2 Швидкість зростання функції. Асимптотичні позначення. Елементарні структури даних. Зв’язані списки доц. Лавренюк А.М.

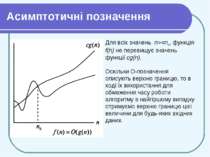
Асимптотичні позначення Аналізуючи будь-який алгоритм, можна намагатись знайти точну кількість дій, що виконує даний алгоритм. Але в більшості випадків достатньо оцінити асимптотику зростання часу роботи алгоритму при прямуванні розміру входу до нескінченності (asymptotic efficiency). Якщо у одного алгоритму швидкість зростання менша, ніж у другого, то в більшості випадків він буде ефективнішим для всіх входів, крім зовсім коротких.

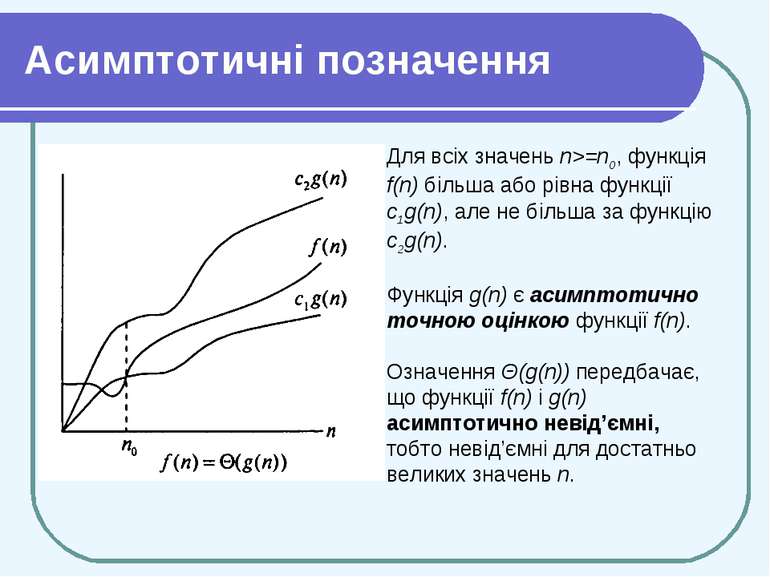
Асимптотичні позначення Час роботи алгоритму сортування методом вставки в найгіршому випадку виражається функцією T(n) = Θ (n2). Для деякої функції g(n) запис Θ(g(n)) означає множину функцій Функція f(n) належить множині Θ(g(n)), якщо існують додатні константи c1 і c2 такі, що дозволяють заключити цю функцію в рамки між функціями c1g(n) і c2g(n) для достатньо великих n. - функція f(n) належить множині Θ(g(n))

Асимптотичні позначення Для всіх значень n>=n0, функція f(n) більша або рівна функції c1g(n), але не більша за функцію c2g(n). Функція g(n) є асимптотично точною оцінкою функції f(n). Означення Θ(g(n)) передбачає, що функції f(n) і g(n) асимптотично невід’ємні, тобто невід’ємні для достатньо великих значень n.

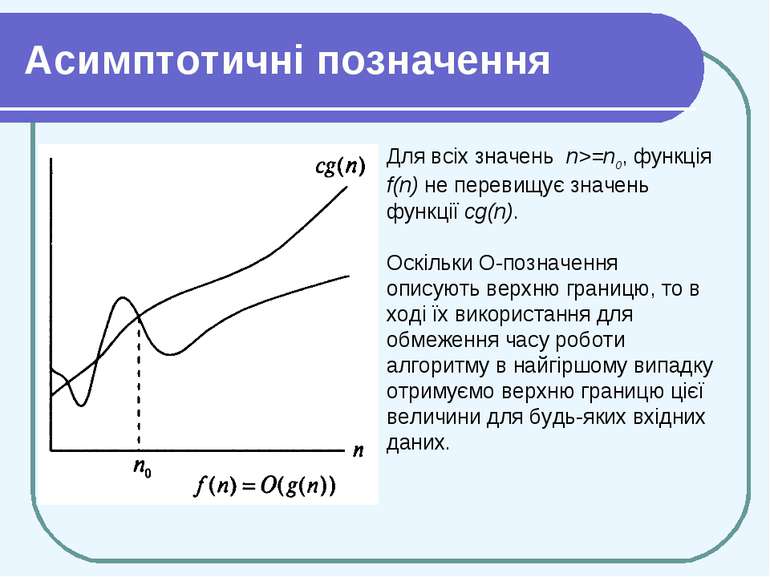
Асимптотичні позначення О-позначення В Θ - позначеннях функція асимптотично обмежується зверху і знизу. Якщо ж достатньо визначити тільки асимптотичну верхню границю, використовуються О - позначення. Для даної функції g(n) позначення О(g(n)) означає множину функцій таких, що Щоб вказати, що функція f(n) належить множині О(g(n)), пишуть f(n) = О (g(n)). Із випливає, що f(n) = О(g(n))

Асимптотичні позначення Для всіх значень n>=n0, функція f(n) не перевищує значень функції cg(n). Оскільки О-позначення описують верхню границю, то в ході їх використання для обмеження часу роботи алгоритму в найгіршому випадку отримуємо верхню границю цієї величини для будь-яких вхідних даних.

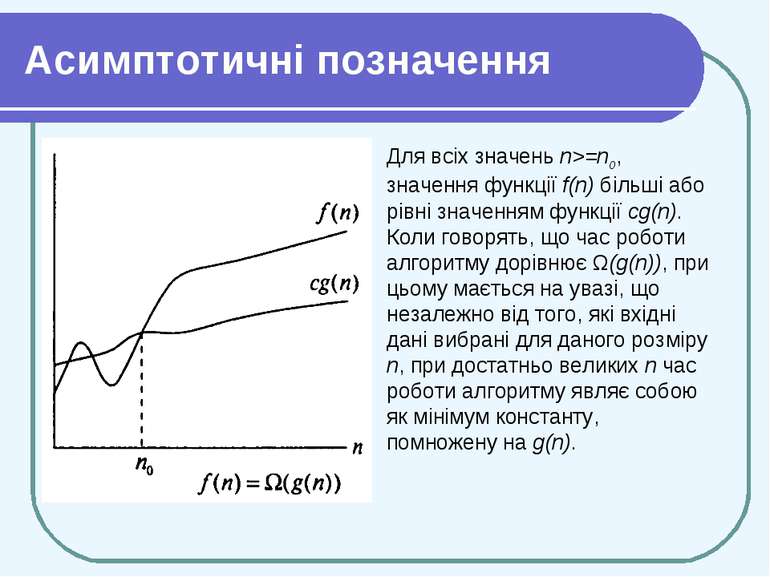
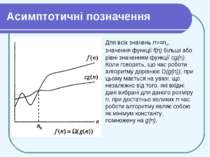
Асимптотичні позначення Ω-позначення Аналогічно тому, як в О-позначеннях дається асимптотична верхня границя функції, в Ω-позначеннях дається її асимптотична нижня границя. Для даної функції g(n) вираз Ω(g(n)) означає множину функцій таких, що Щоб вказати, що функція f(n) належить множині Ω(g(n)), пишуть f(n) = Ω (g(n)).

Асимптотичні позначення Для всіх значень n>=n0, значення функції f(n) більші або рівні значенням функції cg(n). Коли говорять, що час роботи алгоритму дорівнює Ω(g(n)), при цьому мається на увазі, що незалежно від того, які вхідні дані вибрані для даного розміру n, при достатньо великих n час роботи алгоритму являє собою як мінімум константу, помножену на g(n).

Структури даних Структура даних (data structure) — це спосіб зберігання і організації даних, який полегшує доступ до цих даних і їх модифікацію. Множини, які змінюються в процесі виконання алгоритму, називаються динамічними. Елемент динамічної множини — це запис, що містить різні поля. Часто одне з полів розглядається як ключ (key), призначений для ідентифікації елемента, а інші поля — як додаткова інформація (satellite data), що зберігається разом з ключем. Елемент множини шукається за ключем.

Структури даних Операції над динамічними множинами Операції динамічної множини можна розбити на дві категорії: запити (queries), які просто повертають інформацію про множину, і операції-модифікатори (modifying operations), що змінюють множину. Типові операції з множинами такі: Search(S, к) (пошук). Запит, який за даною множиною S і ключем к повертає вказівник на елемент множини S з ключем к. Якщо такий елемент в множині S відсутній, повертається NIL.

Структури даних Операції над динамічними множинами Insert(S, x) Операція-модифікатор, яка поповнює задану множину S одним елементом, на який вказує х (мається на увазі, що до цього моменту всі поля в записі, на який вказує x, вже заповнені). Delete(S, х) Операція-модифікатор, що видаляє із заданої множини S елемент, на який вказує х. (Зверніть увагу, що в цій операції використовується вказівник на елемент, а не його ключове значення.) Minimum(S) Запит до повністю упорядкованої множини S, який повертає вказівник на елемент цієї множини з найменшим ключем.

Структури даних Операції над динамічними множинами Maximum(S) Запит до повністю впорядкованої множини S, який повертає вказівник на елемент цієї множини з найбільшим ключем. Successor(S, x) (наступний) Запит до повністю впорядкованої множини S, що повертає вказівник на елемент множини S, ключ якого є найближчим сусідом ключа елемента х і перевищує його. Якщо ж х - максимальний елемент множини S, то повертається значення NIL. Predecessor(S, x) (попередній) Запит до повністю впорядкованої множини S, що повертає вказівник на елемент множини S, ключ якого є найближчим меншим за значенням сусідом ключа елемента х. Якщо ж х - мінімальний елемент множини S, то повертається значення NIL.

Структури даних Розглянемо різні структури даних (списки, стеки, черги, кореневі дерева), призначені для роботи з динамічними множинами.

Зв’язні списки Зв’язний список (linked list) — це структура даних, у якій об’єкти розташовані у лінійному порядку. Однак, на відміну від масиву, у якому цей порядок визначається індексами, порядок у зв’язному списку визначається вказівниками на кожен об’єкт. Зв’язні списки забезпечують просте й гнучке представлення динамічних множин і підтримують вище перераховані операції.

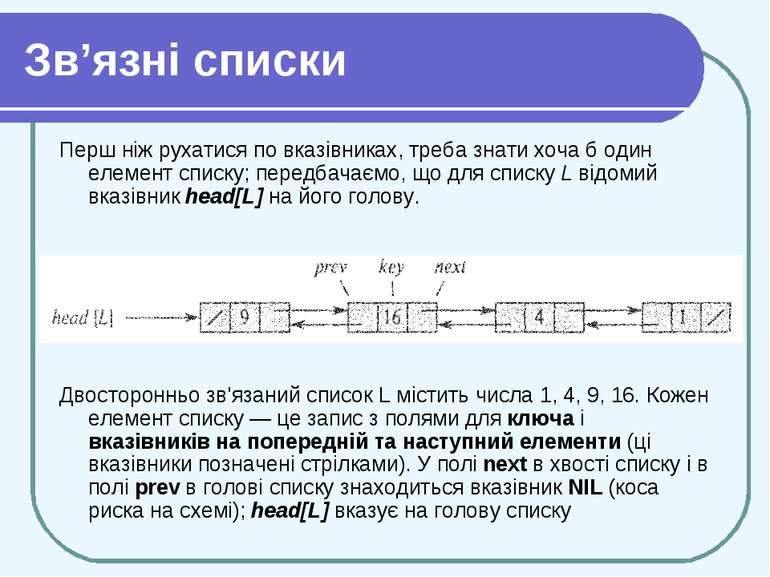
Зв’язні списки У двічі зв’язному списку L (у двозв'язному)(doubly linked list) кожен елемент являє собою об’єкт з одним полем ключа key та двома полями-вказівниками: next (наступний) і prev (попередній). Цей об’єкт може також містити інші супутні дані. Для заданого елемента списку х вказівник next [x] вказує на наступний елемент зв'язаного списку, а вказівник prev [x] — на попередній. Якщо prev [х] = NIL, у елемента х немає попереднього, і, отже, він є першим, тобто головним у списку. Якщо next [x] = NIL, то у елемента х немає наступного, тому він є останнім, тобто хвостовим у списку. head [L] - вказівник на перший елемент списку. Якщо head [L] = =NIL, то список порожній.

Зв’язні списки Перш ніж рухатися по вказівниках, треба знати хоча б один елемент списку; передбачаємо, що для списку L відомий вказівник head[L] на його голову. Двосторонньо зв'язаний список L містить числа 1, 4, 9, 16. Кожен елемент списку — це запис з полями для ключа і вказівників на попередній та наступний елементи (ці вказівники позначені стрілками). У полі next в хвості списку і в полі prev в голові списку знаходиться вказівник NIL (коса риска на схемі); head[L] вказує на голову списку

Зв’язні списки Списки можуть бути різних видів. Список може бути однократно або двічі зв'язним, відсортованим або невідсортованим, кільцевим або некільцевим. Якщо список однократно зв'язаний (однонаправлений) (singly linked), то вказівник prev в його елементах відсутній. Якщо список відсортований (sorted), то його лінійний порядок відповідає лінійному порядку його ключів; у цьому випадку мінімальний елемент знаходиться в голові списку, а максимальний — у його хвості. Якщо список невідсортований, то його елементи можуть розташовуватися в довільному порядку. Якщо список кільцевий (circular list), то вказівник prev його головного елементу вказує на його хвіст, а вказівник next хвостового елементу — на головний елемент. Такий список можна розглядати як замкнутий у вигляді кільця набір елементів.

Зв’язні списки Пошук у зв’язному списку Процедура List_Search(L, k) дозволяє знайти у списку L перший елемент з ключем k шляхом лінійного пошуку, і повертає вказівник на знайдений елемент. Якщо елемент з ключем k у списку відсутній, повертається значення nil.

Зв’язні списки Пошук у зв’язному списку Процедура List_Search(L, 4), викликана для зв'язного списку, зображеного на рис., повертає вказівник на третій елемент, а процедура List_Search(L, 7) — значення nil. Пошук за допомогою процедури List_Search у списку, що складається з n елементів, у найгіршому випадку виконується протягом часу Θ(n), оскільки може знадобитися проглянути весь список.

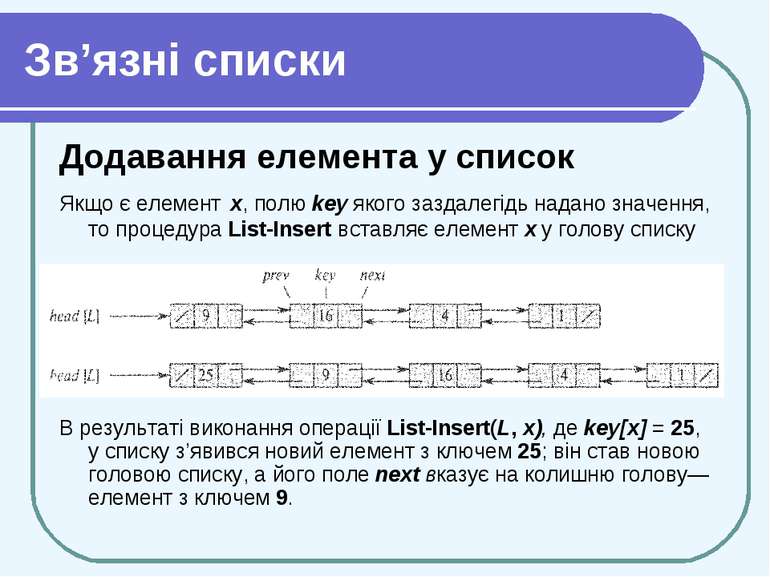
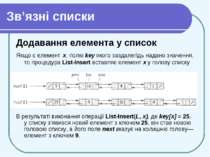
Зв’язні списки Додавання елемента у список Якщо є елемент х, полю key якого заздалегідь надано значення, то процедура List-Insert вставляє елемент х у голову списку В результаті виконання операції List-Insert(L, х), де kеу[х] = 25, у списку з’явився новий елемент з ключем 25; він став новою головою списку, а його поле next вказує на колишню голову— елемент з ключем 9.

Зв’язні списки Додавання елемента у список Час роботи процедури List-Insert дорівнює О(1) (не залежить від довжини списку).

Зв’язні списки Видалення елементу зі списку Процедура List_Delete видаляє елемент х зі зв'язного списку L. У процедуру передається вказівник на елемент х, після чого вона видаляє х зі списку шляхом оновлення вказівників. (Щоб видалити елемент із заданим ключем, необхідно спочатку викликати процедуру List_Search для отримання вказівника на елемент.) Результат виконання операції List-Delete(L, х), де х — вказівник на елемент з ключем 4.

Зв’язні списки Видалення елементу зі списку Час роботи процедури List_Delete дорівнює О(1), але якщо потрібно видалити елемент із заданим ключем, то в найгіршому випадку знадобиться час O(n), оскільки спочатку необхідно викликати процедуру List_Search.

БАЖАЮ УСПІХІВ!!!