Презентація на тему:
Поняття про машинне навчання та Data Mining

Тема №13 Машинне навчання та Data Mining

Машинне навчання: загальний вступ Система навчилась чомусь, якщо вона набула певних знань або умінь, яких раніше не мала. Важливість проблеми; є далекою від повного вирішення.

Рівні навчання: класифікація Уїнстона шляхом програмування; шляхом пояснення; на прикладах; шляхом відкриття.

Навчання на прикладах та індуктивні міркування Навчання на прикладах найтіснішим чином пов'язано з міркуваннями за індукцією.

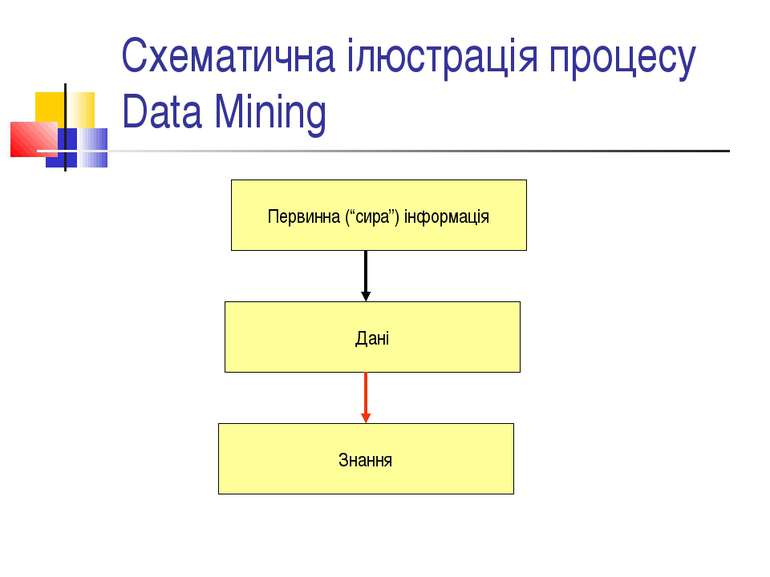
Поняття про Data Mining Інтелектуальний аналіз даних; отримання знань з даних. Одне з визначень: Data Mining - це дослідження і виявлення машиною в “сирих” даних прихованих знань, які раніше не були відомі, нетривіальні, практично корисні, доступні для інтерпретації людиною. “Пояснення” даних; пошук закономірностей.

Схематична ілюстрація процесу Data Mining Первинна (“сира”) інформація Дані Знання

Data Mining: деякі задачі та методики. Регресія; прогнозування. Класифікація (визначення класу об’єкта за його характеристиками). Зокрема, побудова дерев рішень. Пошук асоціативних правил. Алгоритм Apriori. Кластерний аналіз. Нейронні мережі. …

Генетичні алгоритми: вступні слова Важливий підхід до пошуку рішень певної задачі. Типова модель – оптимізаційна задача: f(x1,...xn) -> max при заданих обмеженнях. Втім, оптимальне рішення знаходиться рідко; частіше – якесь наближення. Часто використовуються і для навчання, побудови певних структур тощо. Аналогія з механізмом еволюції, характерним для живої природи.

Генетичні алгоритми: ключова ідея Пов’язуються з дослідженнями Холланда. Імітація еволюційних процесів. Репродукція – створення нових поколінь, селекція – відбір найкраще пристосованих.

Основні поняття Популяція – скінченна множина індивидів (можливих рішень). Хромосома – окремий індивід (рішення); послідовність генів. Ген (можливо, окрема властивість) – атомарний елемент хромосоми. Функція пристосованості (fitness, функція оцінки) – міра пристосованості даного індивіда; цільова функція. На кожній ітерації генетичного алгоритму міра пристосованості кожного індивіда оцінюється саме за допомогою цієї функції. Покоління – чергова популяція в ГА.

Загальна схема класичного генетичного алгоритму випадковим чином ініціалізується початкова популяція з заданою кількістю особин; while (not критерій завершення) { оцінюється пристосованість хромосом у популяції; здійснюється селекція хромосом, які будуть приймати участь у створенні нових особин; найчастіше застосовується алгоритм рулетки; застосовуються генетичні оператори; створюється нова популяція: хромосоми, утворені внаслідок застосування генетичних операторів, включаються до складу нової популяції; } з результуючої популяції вибирається найкраще рішення.

Селекція: алгоритм рулетки Ймовірність відбору кожної хромосоми для формування наступного покоління є пропорційною до міри її пристосованості. Відібрані хромосоми утворюють т.зв. батьківський пул. Варіант – рангова селекція. Крім безумовного застосування алгоритму рулетки, є й інші варіанти (наприклад, елітарна стратегія).

Алгоритм рулетки: формула q – кількість хромосом у популяції; F – міра пристосованості

Турнірна селекція Випадковим чином формуються пари особин, і краща з них перемагає з певною ймовірністю.

Основні генетичні оператори Основний генетичний оператор - кросовер (схрещування) – породження нових індивідів шляхом обміну частинами батьківських хромосом. Застосовується також оператор мутації – випадкова зміна окремих генів хромосоми (можливо, окремих бітів). Ймовірність мутації досить мала (рекомендується до 0,1).

Кросовер: приклад 010|101 та 110|001 дають нащадків: 010|001 та 110|101 (точка розриву вибирається випадковим чином).

ГА: простий ілюстративний приклад Знайти хромосому з найбільшою кількістю одиниць. Вважаємо, що хромосоми містять 12 генів, а популяція нараховує 8 хромосом.

Початкова популяція Ch[1]=[111001100101] Ch[2]=[001100111010] Ch[3]=[011101110011] Ch[4]=[001000101000] Ch[5]=[010001100100] Ch[6]=[010011000101] Ch[7]=[101011011011] Ch[8]=[000010111100]

Оцінка пристосованості F(ch[1])=7 F(ch[2])=6 F(ch[3])=8 F(ch[4])=3 F(ch[5])=4 F(ch[6])=5 F(ch[7])=8 F(ch[8])=5

Селекція хромосом v(ch[1])=15,22 v(ch[2])=13,04 v(ch[3])=17,39 v(ch[4])=6,59 v(ch[5])=8,70 v(ch[6])=10,87 v(ch[7])=17,39 v(ch[8])=10,87 Нехай в результаті випадкового вибору сформовано батьківський пул: Ch[7] Ch[3] Ch[1] Ch[7] Ch[3] Ch[7] Ch[4] Ch[2]

Генетичні оператори Кросовер. Пари: Ch[2] – Ch[7] s=4 Ch[1] – Ch[7] s=3 Ch[3] – Ch[4] s=11 Ch[3] – Ch[7] s=5 Мутація не застосовувалася

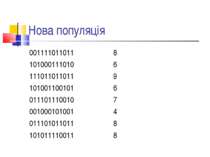
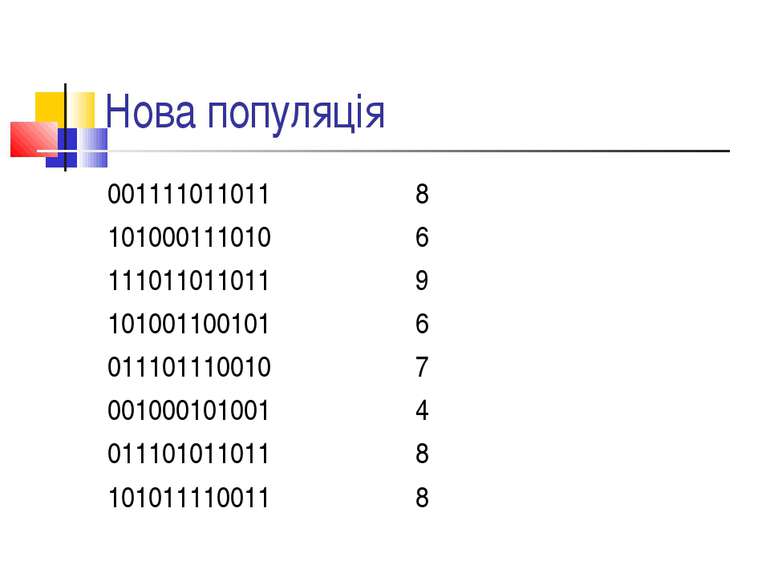
Нова популяція 001111011011 8 101000111010 6 111011011011 9 101001100101 6 011101110010 7 001000101001 4 011101011011 8 101011110011 8

Деякі типові задачі задача про рюкзак; задача коммівояжера.

Особливості задач Для задачі про булевий вираз: бітове представлення. Кросовер: 010|101 та 110|001 дають нащадків: 010|001 та 110|101 (точка розриву вибирається випадковим чином). Мутація - випадкова зміна біту. Для задачі про рюкзак - окремий ген являє собою число предметів кожного типу. Для задачі комівояжера - упорядкований кросовер.

Упорядкований кросовер для задачі комівояжера Дві точки розтину вибираються випадковим чином, але для обох батьків вони співпадають. Нащадки формуються так: спочатку для кожного з них копіюються фрагменти батьківських хромосом між точками розтину; потім кожний нащадок заповнюється містами з іншого батька після другої точки розтину зі збереженням порядку, але вже наявні міста пропускаються. Наприклад, пара (192 | 4657 | 83) та (459 | 1876 | 23) дає нащадків (239 | 4657 | 18) та (392 | 1876 | 45)

Властивості ГА: деякі визначення Тут ми розглядаємо передусім двійкові гени. Схемою назвемо шаблон для формування хромосом, або множину хромосом, в якій нулі та одиниці стоять на заздалегідь визначених позиціях. Охоплення схеми – відстань між першою та останньою постійними позиціями. Порядок схеми – кількість постійних позицій.

Властивості ГА Основним результатом вважається теорема про схеми: схеми малого порядку, з малим охопленням та з пристосованістю вищою за середню формують експоненційно зростаючу кількість своїх представників у наступних поколіннях генетичного алгоритму. Гіпотеза про будівельні блоки: генетичний алгоритм намагається досягти результату, близького до оптимального, за рахунок комбінування “хороших” схем малого порядку та з малим охопленням. Такі схеми називаються будівельними блоками (цеглинками). “Хороші” схеми – це нібито вдалі комбінації ознак, які мають бути збережені в наступних поколіннях.

Пошук аналогій Одна з типових постановок задач: якщо А1, то Q1; A2 схоже на А1. Що, якщо А2 ? Типова схема: пошук схожостей (або відмінностей); модифікація дії на основі списку схожостей.

Задача Еванса Дані малюнки А, В, С. Знайти малюнок Х, який відноситься до С так само, як В до А.

Схема рішення Схема рішення: Потрібно знайти послідовність операцій f, яка переводить А до В, і послідовність g, яка переводить А до С. Далі або X1=g(B), або X2=f(C). Якщо Х1=Х2, рішення, отримані обома способами, співпадають, і утворюється т.зв. "квадрат Лейбніца".

Засвоєння понять Загальна постановка задачі: сформувати опис поняття, такий, що всі позитивні навчальні приклади відповідають цьому опису, а всі негативні (контрприклади) не відповідають. Формується деякий початковий опис, який коригується за певними правилами при надходженні прикладів і контрприкладів. Алгоритм Уїнстона: специфічний підбір прикладів та контрприкладів. Мітчелл: пошук в просторі версій, алгоритм виключення кандидата.

Алгоритм Мітчелла - основи Ключова ідея методики Мітчелла засвоєння понять – формування правила, яке описує певне поняття, на основі пошуку в просторі версій (просторі понять). При цьому правило (опис поняття) слід розуміти як деяку логічну функцію, яка повинна бути істинною для всіх позитивних прикладів та хибною – для всіх негативних. Версія – це певний кандидат на те, щоб бути остаточним варіантом опису. Важливо – версії формують простір версій, упорядкований на основі відношень "більш загальна версія" та "менш загальна версія". Це робить пошук більш спрямованим.

Відношення узагальнення в просторі версій Версія h1 є більш загальною, ніж версія h2, якщо множина об'єктів, які задовольняють описові h2, є підмножиною об'єктів, які задовольняють описові h1. Наприклад: (X,color,red) та (ball,color,red). Кажуть також, що в цьому випадку h1 покриває h2. Зворотне відношення – більш спеціалізована версія.

Отримання більш загальних версій: основні шляхи Заміна конкретних значень змінними. Вилучення умов з кон'юнктивних виразів. Додавання диз'юнкцій. Заміна підкласу на надклас.

Алгоритм виключення кандидата – загальні принципи Підтримуються дві множини – G – множина найбільш загальних версій; S – множина найбільш спеціалізованих версій. При отриманні позитивного прикладу відбувається перехід до більш загальних версій. При отриманні контрприкладу відбувається перехід до більш спеціалізованих версій.

Приклад: формування поняття “red ball” G: {obj(X,Y,Z)} S: {} Позитивний: obj(small, red, ball) G: {obj(X,Y,Z)} S: {obj(small,red,ball)} Негативний: obj(small, blue, ball) G: {obj(X,red,Z)} S: {obj(small,red,ball)} Позитивний: obj(large, red, ball) Негативний: obj(large, red, cube) G: {obj(X,red,Z)} S: {obj(X,red,ball)} S=G: {obj(X,red,ball)}

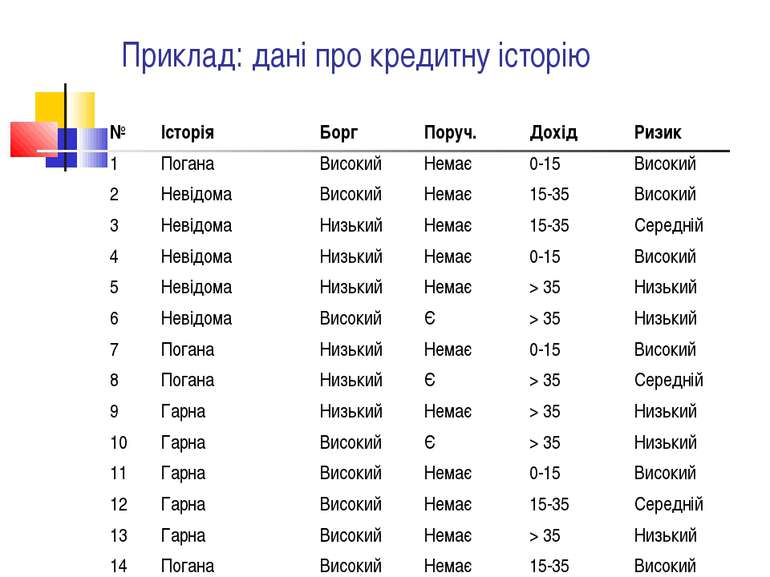
Поняття про дерева рішень Одна з найбільш відомих та поширених методик навчання на прикладах. Базовий метод – ID3. Дана навчальна вибірка, яка містить ознаки деяких об'єктів з різних класів. Задача: отримати правила, які дозволяють відносити нові об'єкти до того чи іншого класу. Класичний приклад: оцінка кредитного ризику на основі даних про кредитну історію, поточний борг, наявність поручительства та дохід потенційного клієнта.

Приклад: дані про кредитну історію № Історія Борг Поруч. Дохід Ризик 1 Погана Високий Немає 0-15 Високий 2 Невідома Високий Немає 15-35 Високий 3 Невідома Низький Немає 15-35 Середній 4 Невідома Низький Немає 0-15 Високий 5 Невідома Низький Немає > 35 Низький 6 Невідома Високий Є > 35 Низький 7 Погана Низький Немає 0-15 Високий 8 Погана Низький Є > 35 Середній 9 Гарна Низький Немає > 35 Низький 10 Гарна Високий Є > 35 Низький 11 Гарна Високий Немає 0-15 Високий 12 Гарна Високий Немає 15-35 Середній 13 Гарна Високий Немає > 35 Низький 14 Погана Високий Немає 15-35 Високий

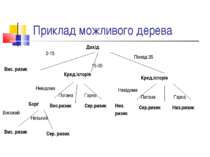
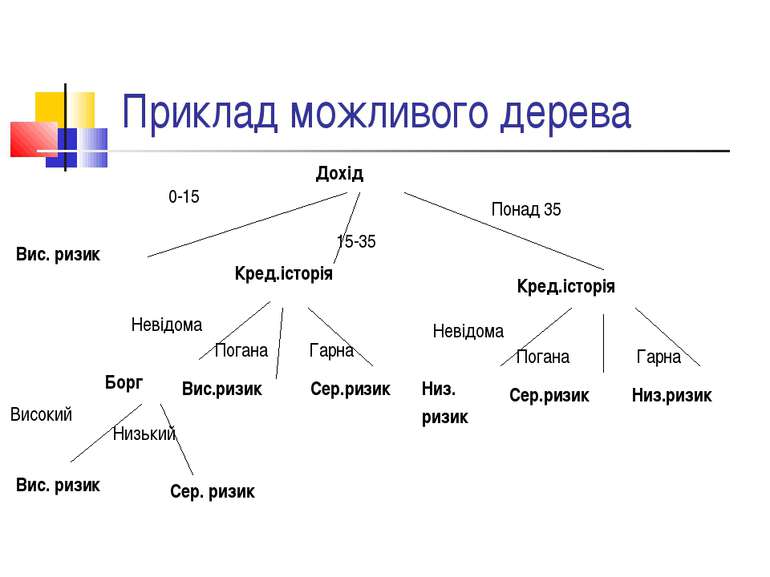
Приклад можливого дерева Дохід 15-35 Вис. ризик Кред.історія Кред.історія 0-15 Понад 35 Борг Невідома Високий Вис. ризик Низький Сер. ризик Вис.ризик Погана Гарна Сер.ризик Низ. ризик Невідома Сер.ризик Погана Гарна Низ.ризик

Дерева рішень: принцип побудови Дерево побудоване за таким принципом: кожний внутрішній вузол відповідає певній властивості та по суті передбачає розподіл за цією властивістю - підмножини, що утворюються внаслідок такого розподілу, мають спільне значення цієї властивості. Дуга - можливе значення властивості. Листки - кінцеві рішення. З іншого боку, шлях від кореня до листка можна інтерпретувати як окреме правило прийняття рішень.

Алгоритм побудови дерева рішень (ID3) function induce_tree (Example_Set, Properties) begin якщо всі елементи набору прикладів Example_Set належать до одного класу - повернути листовий вузол, віднісши його до цього ж класу; else якщо множина Properties пуста - повернути листовий вузол, ім'я якого - об'єднання всіх імен класів в Example_Set; else begin вибрати властивість А та призначити її коренем поточного дерева; видалити властивість А з множини Properties; для кожного значення V властивості А begin створити дугу дерева з міткою V; до підмножини partition#V віднести елементи множини Example_Set, для яких властивість А приймає значення V; рекурсивно викликати функцію induce_tree(partition#V, Properties); додати результати до гілки V; end; end; end;

Вибір властивості для розбиття На основі теорії інформації. Слід вибирати найбільш інформативну ознаку, тобто таку, розбиття за якою дає найбільший інформаційний виграш.

Математично: Оцінка необхідної інформації: Інформація, необхідна для завершення побудови дерева після вибору властивості Р, яка розбиває множину C на С1, … Сn: Потрібно вибирати властивість Р, яка максимізує величину інформаційного виграшу Gain(P) = I(M) – Q(P)

Модифікації ID3 Алгоритм С4.5

Навчання з підкріпленням Загальний принцип – агент взаємодіє з оточуючим середовищем. Він вибирає дії, як наслідок отримує від середовища заохочення або покарання та на основі цього коригує свою поведінку. Більш формально – в певний момент часу агент знаходиться в деякому стані S з множини станів S = {s1, … , sn}. На будь-якому кроці він вибирає з множини можливих дій A певну дію a (цей вибір залежить від стану). У відповідь він отримує результат r та переходить до деякого іншого стану s’. Після певної кількості подібних експериментів агент має дослідити оточуюче середовище та вибрати оптимальну поведінку.

Автомати з лінійною тактикою Певна кількість груп станів; кожна група відповідає окремій дії. Кожна група має по q станів; q – глибина пам'яті автомата. При отриманні заохочення – перехід до більш глибокого стану цієї ж групи, при отриманні покарання – до менш глибокого стану цієї ж, або до найменш глибокого стану іншої групи.