Презентація на тему:
”КОМП’ЮТЕРНІ МЕТОДИ РОЗРАХУНКІВ В ОПТИЦІ”

Дисципліна ”КОМП’ЮТЕРНІ МЕТОДИ РОЗРАХУНКІВ В ОПТИЦІ” Доцент кафедри ФОЕТ, канд. физ.-мат. наук ФРОЛОВА Тетяна Іванівна Web-сторінка: http://frolova.zzl.org E-mail: frolova@kture.kharkov.uaа ауд. 115і, тел. 7021057 Харківський національний університет радіоелектроніки

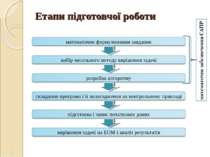
Лекція №10 “Математичні моделі об'єктів проектування.” Етапи підготовки для виконання інженерних розрахунків. Побудова математичних моделей об'єктів проектування. Основні вимоги до математичних моделей. Розробка алгоритмів і форми їх подання. Ієрархія математичних моделей у САПР. *

Етапи підготовчої роботи *

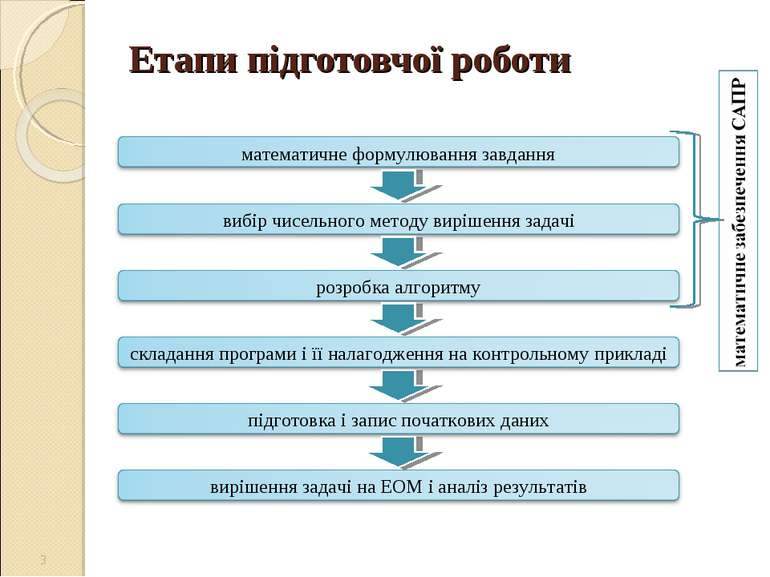
Математична модель Математичне формулювання завдання включає математичний опис її умов і визначення аналітичних виразів і формул, що підлягають вирішенню на ЕОМ. Остаточний вигляд формул і математичних залежностей звичайно називають математичною моделлю. Математична модель (ММ) - це сукупність математичних об'єктів (чисел, змінних, векторів, множин і т. п.) і відносин між ними, яка адекватно відображає деякі властивості проектованого технічного об'єкта. Головною вимогою до математичних моделей є адекватність відображення в них модельованого об'єкта. *

Побудова математичної моделі Математичні моделі, що використовуються при проектуванні різних технічних об'єктів, мають загальну структуру. ММ як і об'єкт проектування характеризується своїми параметрами: вихідними (вектор Y), внутрішніми (вектор X) і зовнішніми (вектор Q). У загальному випадку математична модель записується у вигляді:  Y=F(X,Q),  де F – деяка вектор-функція. В більшості випадків зв'язок між вихідними, внутрішніми і зовнішніми параметрами відома не у вигляді явної функціональної залежності, а задається в алгоритмічній формі, наприклад через чисельне вирішення системи рівнянь. Побудова математичних моделей різних технічних об'єктів є досить складним творчим процесом, що вимагає від розробника знання тієї області, до якої відноситься проектований об'єкт, методів математичного моделювання і певної винахідливості. *

Змінні в математичних моделях Всі змінні в математичних моделях діляться на три групи: керовані, некеровані й похідні. Під керованими змінними розуміють такі, вибір конкретних значень яких визначає вибір того або іншого проектного рішення. Некеровані змінні характеризують ситуацію, в якій повинне бути ухвалене рішення. Ці змінні описують зовнішні чинники, не залежні від проектних рішень, що оптимізуються, але що впливають на наслідки ухвалення того чи іншого вирішення. Похідні змінні, залежні від керованих і некерованих змінних, є результатами ухвалення того або іншого проектного рішення. До таких змінних у проектних завданнях відносяться техніко-економічні характеристики проектованого об'єкта. *

Якісні і кількісні цілі проектних рішень В основу процесу вибору проектних рішень на різних етапах закладають досягнення деяких цілей, які можна підрозділити на якісні й кількісні. Під якісними маються на увазі цілі, яким відповідають лише два результати - мета досягнута або не досягнута. Співвідношення, що описують умову здійснення якісних цілей, звичайно називають обмеженнями моделі (технічними обмеженнями), а вирішення, що задовольняють цим умовам, - допустимими, тому цей тип критеріїв називають іноді критеріями допустимості. Під кількісними мають на увазі такі цілі, які полягають у прагненні збільшити (або зменшити) деякі характеристики проектованого об'єкта, залежні від схвалюваних вирішень. Критерії, які служать для відображення кількісних цілей, називають критеріями ефективності або приватними критеріями ефективності. *

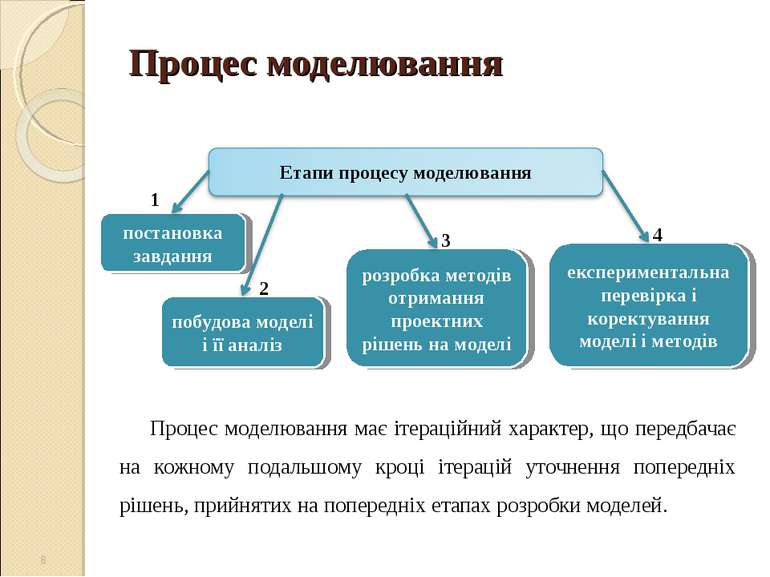
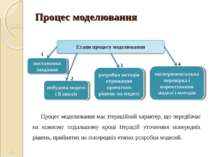
Процес моделювання Процес моделювання має ітераційний характер, що передбачає на кожному подальшому кроці ітерацій уточнення попередніх рішень, прийнятих на попередніх етапах розробки моделей. *

Основні вимоги до ММ Адекватність ММ — це відповідність моделі модельованому об'єкту (процесу). Причому адекватність розглядають по тих властивостях моделі, які для конструктора або технолога є необхідними в даний момент. Під адекватністю ММ також розуміють здатність відображати задані властивості об'єкту проектування з поточною похибкою не вище заданої похибки 0. Точність ММ визначає міру збігу значень параметрів реального об'єкту і значень тих же параметрів, отриманих на основі досліджуваної ММ. Точність моделі оцінюється відносною похибкою: де yм – вихідний параметр, розрахований за допомогою моделі; yист – той же вихідний параметр, що має місце в модельованому об'єкті. Універсальність моделі визначається числом і складом зовнішніх і вихідних параметрів, що враховуються в моделі. Із збільшенням зовнішніх чинників розширюється застосовність моделі, але при цьому ускладнюється її розробка. Економічність ММ зазвичай характеризують витратами обчислювальних ресурсів ЕОМ при їх реалізації, враховуючи машинний час і об'єм пам'яті, що використовується. *

Розробка математичних моделей Складання математичного опису полягає у встановленні зв'язків між параметрами процесу і виявленні його граничних і початкових умов, а також у формалізації процесу у вигляді системи математичних співвідношень, що характеризують об'єкт, який вивчається. При моделюванні складних систем можливі наступні випадки. Система, що моделюється, досить добре вивчена, і дозволяє записати аналітичні співвідношення, які і служитимуть моделлю. Математична модель відома з точністю до невідомих параметрів , для обчислення яких проводяться необхідне число експериментів. Відомо, що моделлю може служити одна з функцій i(x, i) (i=1,2,…l). Аналітичний вигляд моделі не відомий взагалі. *

Математичне моделювання Математичне моделювання можливе якщо: складно підтримувати одні і ті ж робочі режими при кожному повторенні експерименту на працюючому устаткуванні або протягом всього часу проведення серії експериментів; для здобуття однієї і тієї ж величини вибірки можуть бути потрібні надмірні витрати часу і засобів; при експериментуванні з реальними системами неможливе дослідження безлічі альтернативних варіантів, які пов'язані з аварійними або небезпечними технологічними режимами; є упевненість в успішному створенні моделі системи або операції, що вивчається. Для цього слід заздалегідь мати можливість збору необхідної кількості інформації про елементи і зв'язки в модельованій системі, що забезпечує достовірність процесу моделювання; є можливість (і необхідність) побічного використання процесу побудови моделей елементів системи для їх дослідження; всі інші методи рішення непридатні. *

Чисельні методи Чисельні методи дозволяють звести вирішення найрізноманітніших і складних операцій (інтеграція, диференціювання, обчислення логарифмічних і інших функцій) до послідовного виконання чотирьох арифметичних дій. Для різних математичних завдань, використовуваних в САПР, розроблені чисельні методи їх вирішення. Вибір того чи іншого чисельного методу для вирішення завдання на ЕОМ пов'язаний з вимогами, по-перше, постановкою завдання (необхідна точність, швидкість рішення і витрати на підготовку програми) і, по-друге, самою ЕОМ і програмою з позиції реалізації методу на машині. За отриманими математичними залежностями записують послідовність виконання математичних операцій у вигляді алгоритму. На етапі вибору чисельного методу вирішення завдання вибирають методи оптимізації виходячи з вигляду цільової функції, кількості й характеру змінних та ін. *

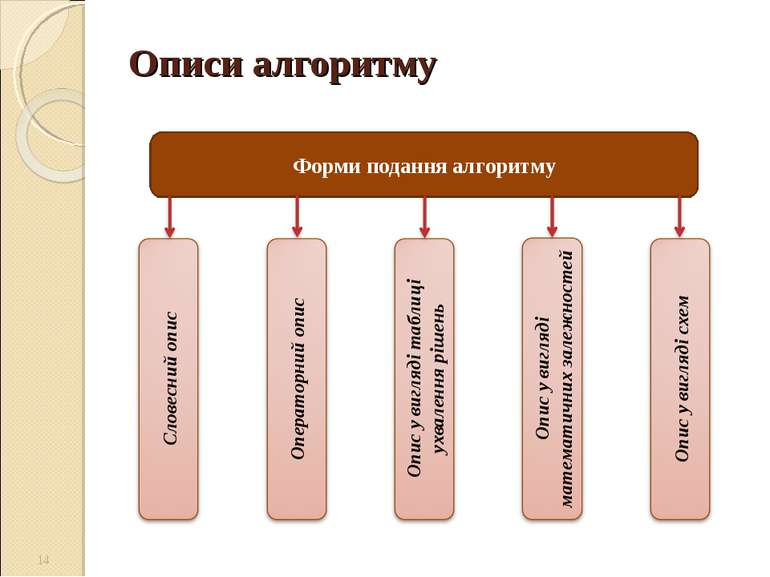
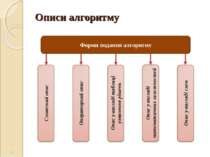
Розробка алгоритмів Під алгоритмом розуміють певну, строго визначену послідовність виконання процесу, направленого на отримання бажаної інформації певного вигляду і обсягу. Алгоритм характеризується наступними поняттями: детермінованістю, дискретністю, масовістю і формалізацією. Детермінованість, або визначеність встановлює однозначність результату процесу при заданих початкових даних і показує, що не можуть бути його різні тлумачення. Дискретність означає розчленованість алгоритму на окремі елементарні дії. Масовість припускає вирішення будь-якої задачі з класів однотипних при різних значеннях початкових даних. Під формалізацією, точніше ступенем формалізації слід розуміти рівень наближення розробки алгоритму до мови програмування. Можна вважати, що алгоритм достатньо формалізований тоді, коли він може бути запрограмований для ЕОМ з використанням існуючого математичного забезпечення. *

Описи алгоритму *

Ієрархія ММ у САПР Залежно від міри деталізації описуваних властивостей і процесів, що протікають в об'єкті, функціональні моделі розділяють на: ММ на мікрорівні (ММ з розподіленими параметрами); ММ на макрорівні (ММ із зосередженими параметрами); ММ на метарівні. Моделі мікрорівня описують фізичні процеси в елементі; Моделі макрорівня описують процеси прояву зовнішніх властивостей елементів при їх взаємодії між собою і зовнішнім середовищем у функціональному вузлі; Моделі метарівня описують інформаційні процеси в укрупнених функціональних вузлах, структурних блоках з використанням апарату аналізу систем автоматичного управління, математичної логіки, теорії кінцевих автоматів; *

Мікро-, макро- та метарівні На мікрорівні ММ представлені диференціальними рівняннями в частинних похідних (ДРЧП) разом з краєвими умовами. На макрорівні розробляється дискретизація простору з виділенням в якості елементів окремих деталей. Така дискретизація означає перехід від розподілених моделей до зосереджених. При цьому з числа незалежних змінних виключають просторові координати, незалежною змінною тут залишається лише час. На метарівні за допомогою подальшого абстрагування від характеру фізичних процесів вдається отримати прийнятний по складності опис процесів, що протікають в проектованих об'єктах. Математичні моделі на метарівні — це системи звичайних диференціальних рівнянь, системи рівнянь алгебри, системи логічних рівнянь, імітаційні моделі систем масового обслуговування. *

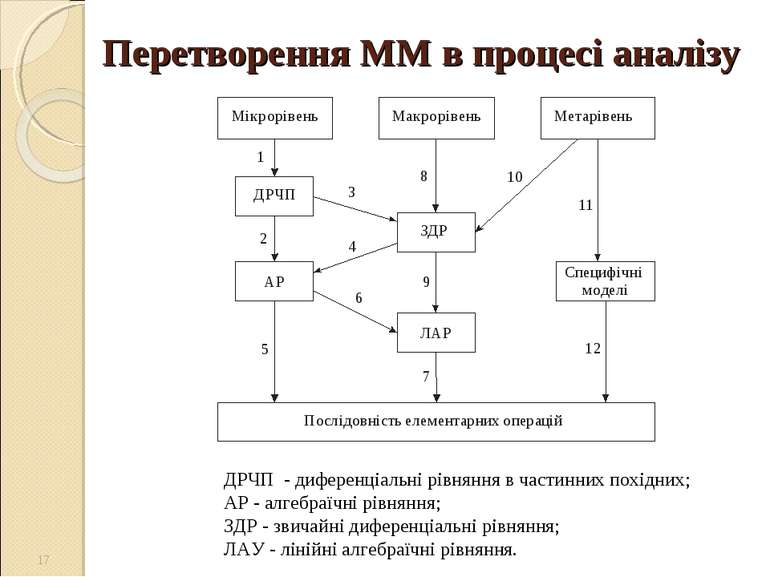
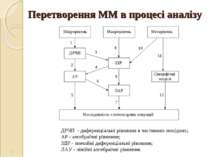
Перетворення ММ в процесі аналізу * ДРЧП - диференціальні рівняння в частинних похідних; АР - алгебраїчні рівняння; ЗДР - звичайні диференціальні рівняння; ЛАУ - лінійні алгебраїчні рівняння.

Питання для підготовки * Що таке математична модель? Які основні вимоги до математичних моделей? У чому полягає суть побудови математичного моделювання об'єктів проектування? З чого складається процес розробки алгоритмів? Ієрархія математичних моделей у САПР? Приведіть схему перетворення ММ в процесі аналізу?