Презентація на тему:
трикутник його властивості

Трикутник і його елементи. Види трикутників.

B Які фігури уже вам знайомі з курсу геометрії? Чи знаєте ви властивості цих фігур?

Історична довідка Трикутник – найпростіша фігура: три вершини й три сторони. Перші відомості про трикутник та його властивості ми знаходимо в єгипетських папірусах, яким більше 4000 років. У них зокрема, згадується спосіб знаходження площі рівнобедреного трикутника. Через 2000 років у Стародавній Греції вивчення властивостей трикутника досягає високого рівня. У XV—XVI ст. з'явилася величезна кількість досліджень властивостей трикутника, які ввійшли в розділ планіметрії, що одержав назву «Нова геометрія трикутника». Великий внесок у розвиток геометрії трикутника внесли мате матики XIX—XX ст.: Лемуан, Брокар, Тебо й ін. Сьогодні ми ознайомимось з такою геометричною фігурою як трикутник, розглянемо з яких елементів він складається, його види, дамо їм назву навчимося розв’язувати задачі.

Фалес Мілетський пр. 624 до н.е. – 548 до н.е. Вважається, що Фалес першим познайомив греків з геометрією. Йому приписують відкриття і доведення ряду теорем одна з яких про рівність кутів при основі рівнобедреного трикутника. Фалес установив, що трикутник повністю визначається стороною і прилеглими до неї кутами.

Піфагору та учням його школи належать вчення про прямокутний трикутник. У I книзі Начала вивчаються властивості трикутників, цю книгу вінчає знаменита теорема Піфагора для прямокутних трикутників. Серед "визначень", якими починається ця книга, є і такі: "З тристоронніх фігур рівносторонній трикутник є фігура, яка має три рівні боки, рівнобедрений - має тільки дві рівні сторони, різнобічний - має три нерівні сторони". Піфагор Народився: пр. 580 – 572 до н. е. Помер: пр. 500 – 490 до н. е.

Герон Александрійський Народився: пр. У 1 ст. н.е. Найбільш відома формула для знаходження площі трикутника – це формула Герона). Ще в І столітті давньогрецький вчений Герон запропонував знак для позначення трикутників. Зображення трикутників і завдання на трикутники зустрічаються в папірусах, в старовинних індійських книгах та інших древніх документах. Слово “трикутник” античного походження. Знак почали застосовувати в ІV столітті.

Трикутник Пенроуза або трибар Трикутник Паскаля Бермудський трикутник

Уже кілька тисяч років тому єгиптяни знали, що коли сторони трикутника дорівнюють 3, 4 і 5 одиничним відрізкам, то такий трикутник прямокутний. Землеміри Стародавнього Єгипту для побудови прямого кута ділили мотузку вузликами на 12 рівних частин і кінці зав’язували. Ребра бічних граней єгипетських пірамід утворюють майже рівносторонні трикутники.

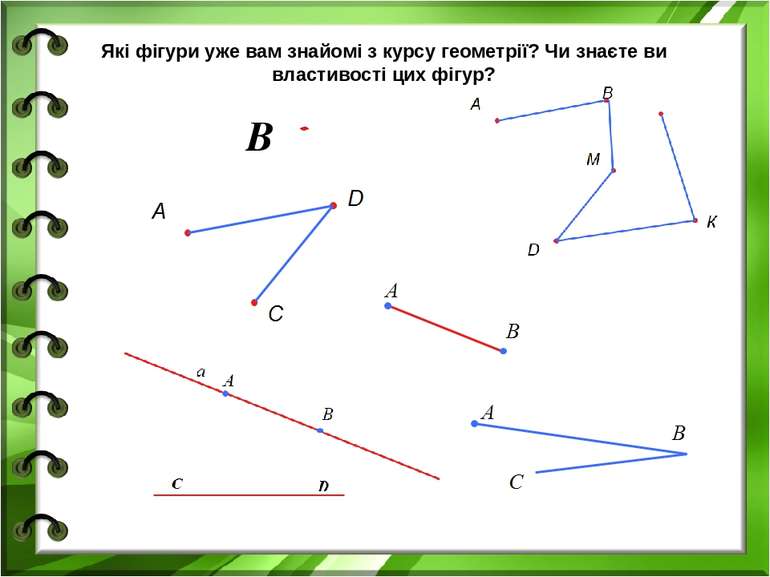
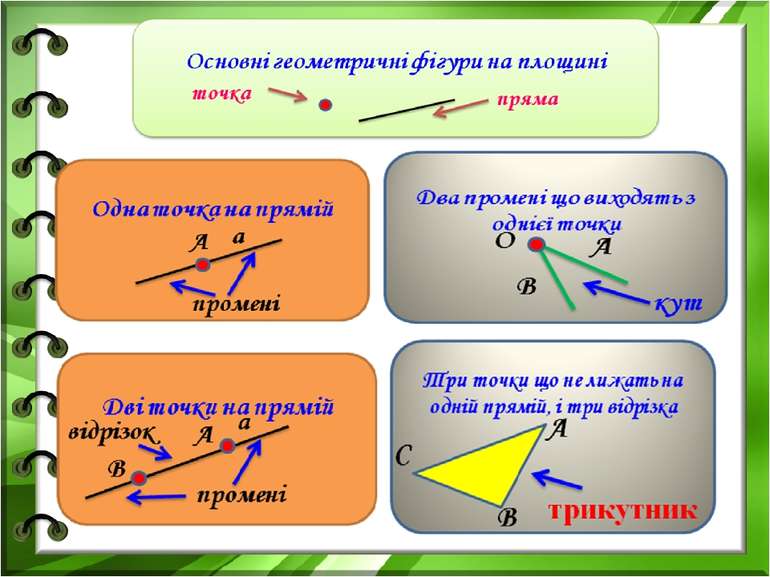
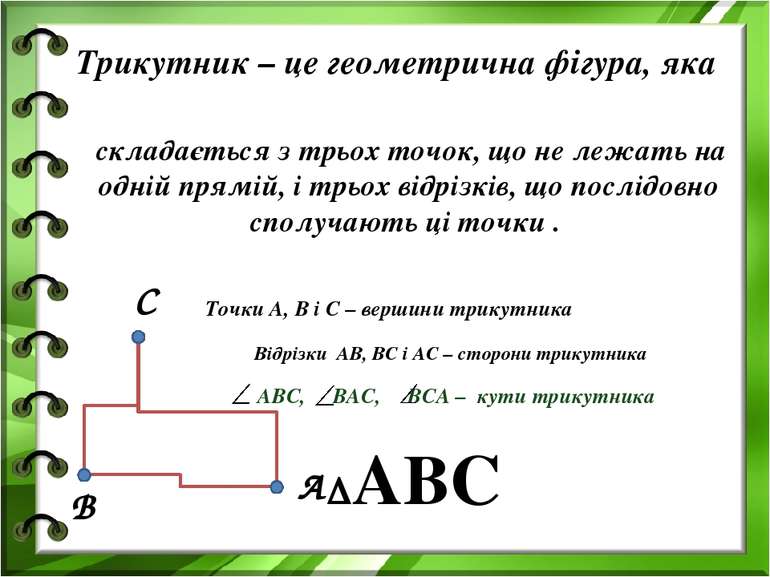
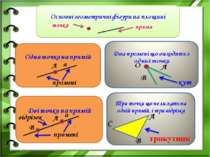
В А С Точки А, В і С – вершини трикутника Відрізки АВ, ВС і АС – сторони трикутника ΔАВС складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, що послідовно сполучають ці точки . Трикутник – це геометрична фігура, яка АВС, ВАС, ВСА – кути трикутника

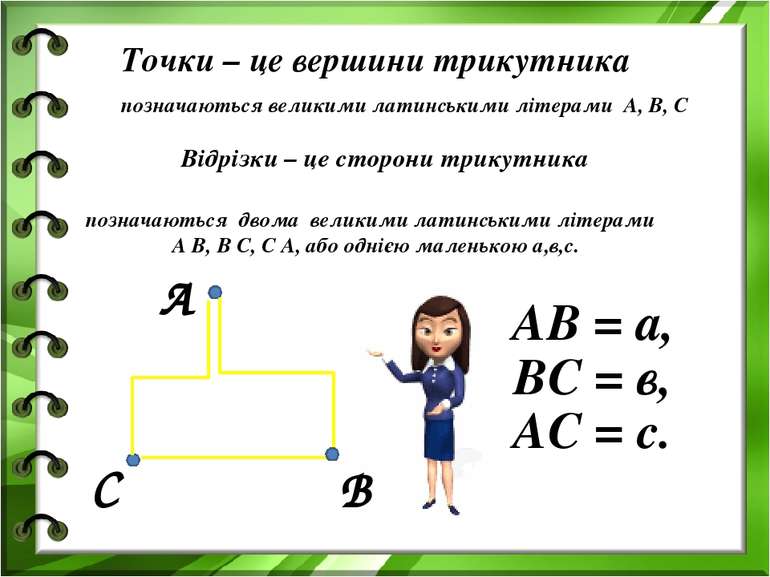
Точки – це вершини трикутника Відрізки – це сторони трикутника позначаються великими латинськими літерами А, В, С А В С позначаються двома великими латинськими літерами А В, В С, С А, або однією маленькою а,в,с. АВ = а, ВС = в, АС = с.

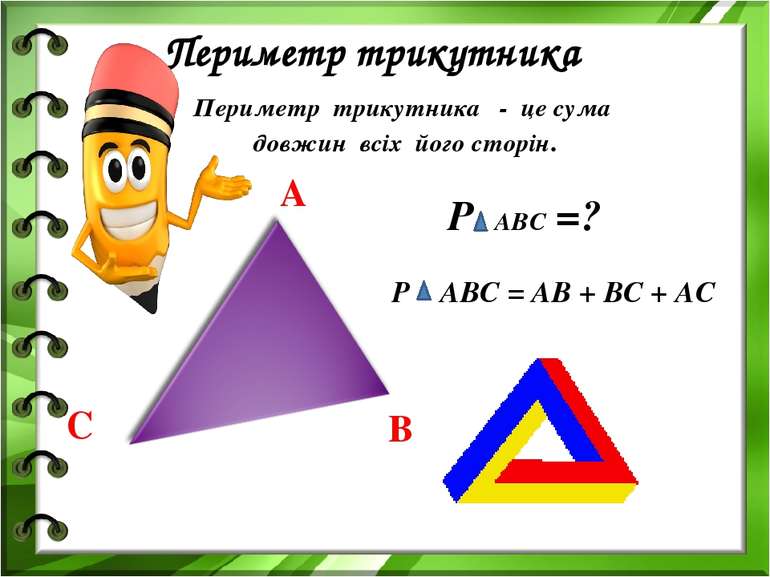
Периметр трикутника Периметр трикутника - це сума довжин всіх його сторін. P ABC =? P ABC = AB + BC + AC А В С

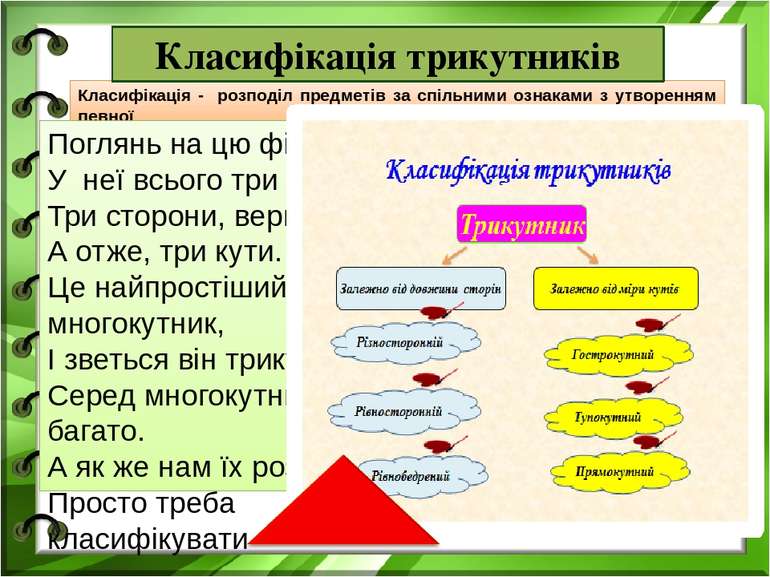
Класифікація - розподіл предметів за спільними ознаками з утворенням певної системи класів. Класифікація трикутників Поглянь на цю фігуру У неї всього три - Три сторони, вершини, А отже, три кути. Це найпростіший многокутник, І зветься він трикутник. Серед многокутників багато. А як же нам їх розпізнати? Просто треба класифікувати

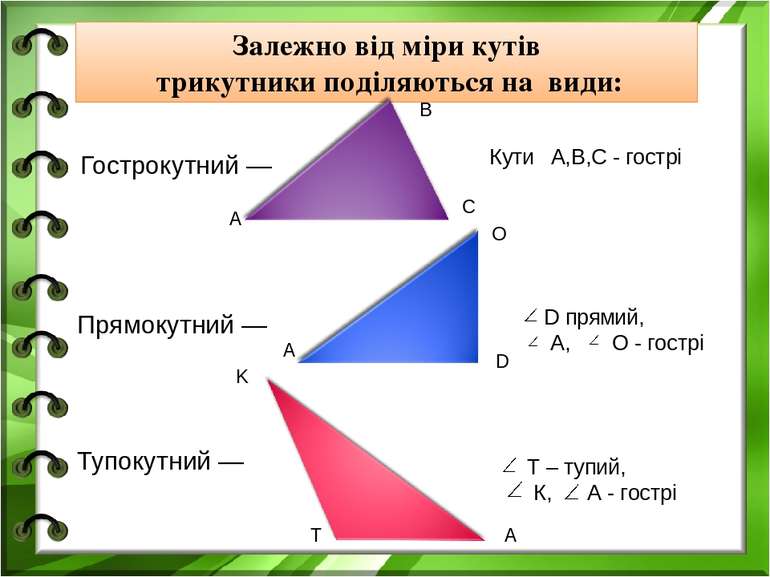
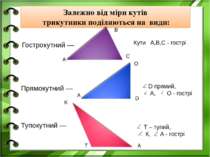
Залежно від міри кутів трикутники поділяються на види: Прямокутний — Тупокутний — А В С А О D K T A Кути A,B,C - гострі D прямий, A, O - гострі Т – тупий, К, А - гострі Гострокутний —

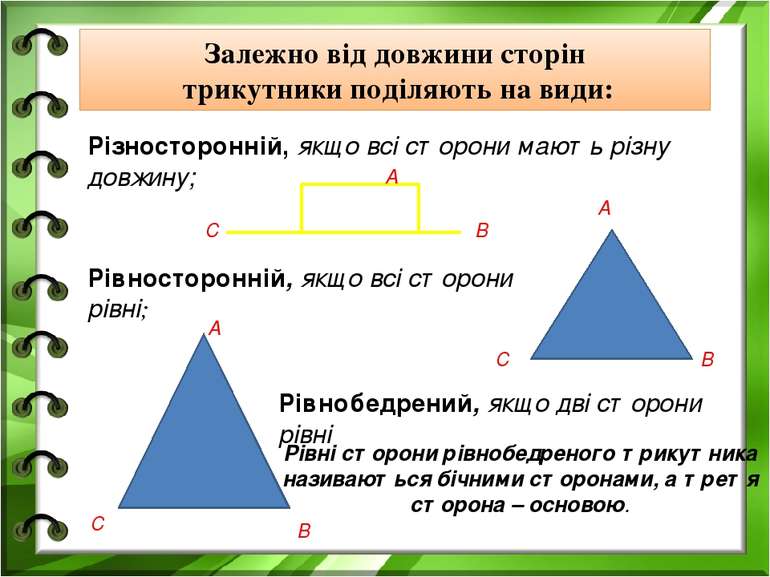
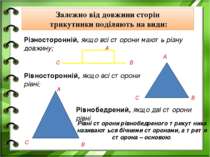
Залежно від довжини сторін трикутники поділяють на види: Різносторонній, якщо всі сторони мають різну довжину; Рівносторонній, якщо всі сторони рівні; Рівнобедрений, якщо дві сторони рівні Рівні сторони рівнобедреного трикутника називаються бічними сторонами, а третя сторона – основою. А В С А В С А В С

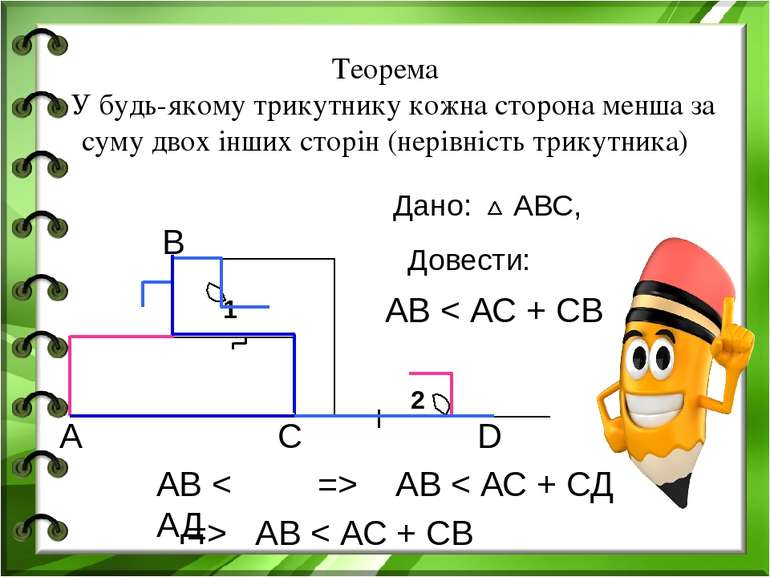
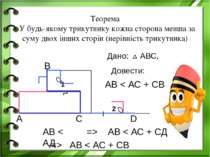
Теорема У будь-якому трикутнику кожна сторона менша за суму двох інших сторін (нерівність трикутника) А В С D АВ < АС + СВ Довести: 1 2 АВ < АД => АВ < АС + СД => АВ < АС + СВ Дано: АВС,

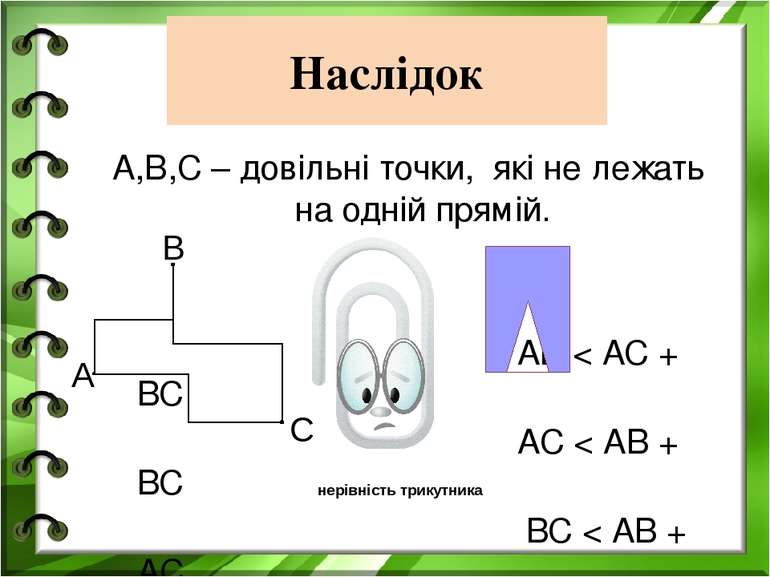
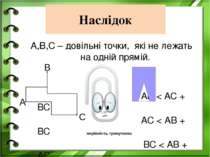
Наслідок А,В,С – довільні точки, які не лежать на одній прямій. АВ < АС + ВС АС < АВ + ВС ВС < АВ + АС А В С нерівність трикутника

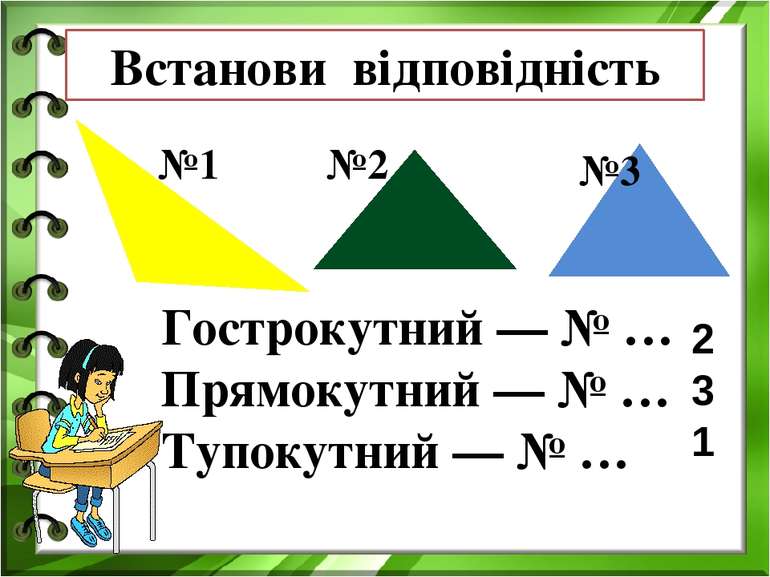
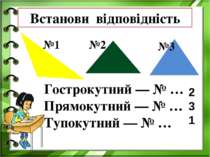
Гострокутний — № … Прямокутний — № … Тупокутний — № … №1 №2 №3 Встанови відповідність 2 3 1

№1 №2 №3 Рівнобедрений — №… Рівносторонній — №… Різносторонній — № … Встанови відповідність 2 1 3

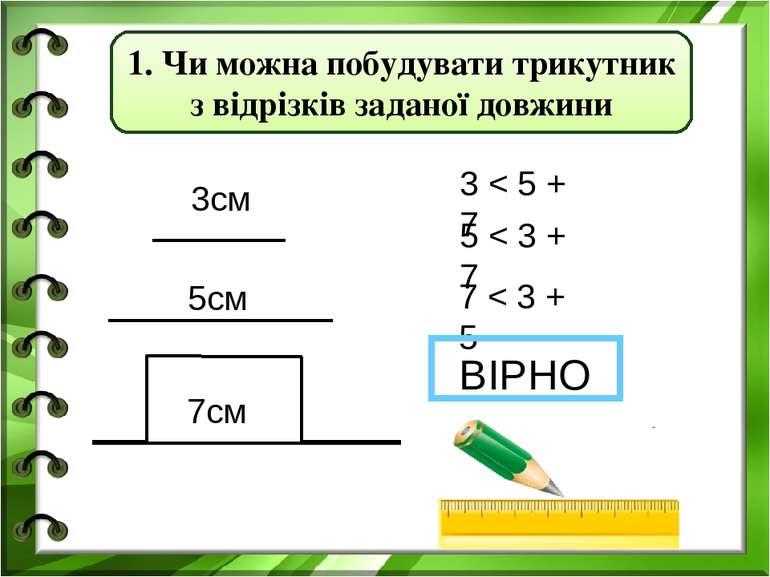
3см 5см 7см 3 < 5 + 7 5 < 3 + 7 7 < 3 + 5 ВІРНО 1. Чи можна побудувати трикутник з відрізків заданої довжини

2см 4см 6см 6 =2 + 4 НІ 2. Чи можна побудувати трикутник з відрізків заданої довжини

1см 3см 5см 5 < 1 + 3 НІ 3. Чи можна побудувати трикутник з відрізків заданої довжини

Задача 1. Знайдіть периметр трикутника ∆АВС АВ=5 см, АС=3см, ВС=6 см (Р= АВ+АС+ВС=5+3+6=14см) (Р= АВ+АС+ВС=5+5+5=15см); АВ=АС=ВС=5 см Задача 2. Василько з куска дроту, довжиною 24см зігнув фігуру - рівносторонній трикутник. Який периметр цього трикутника? Яка довжина сторони?

РЕФЛЕКСІЯ • Сьогодні я на уроці ….. • Я дізнався….. • Я поглибив…… • Мені нам уроці сподобалося….. • Мене дуже здивувало….. • Мене найбільше вразило…. • Я вирішив дізнатися більше про…. • Я вважаю дану тему….. • Дані знання допоможуть мені під час…

Домашнє завдання 1. Вивчити означення та властивості сторін трикутника. 2. Задача. Периметр трикутника ABC дорівнює 26 м, причому АВ = 10 м, а сторона ВС втричі менша, ніж сторона АС. Знайдіть невідомі сторони трикутника ABC. 3. Підготувати розповідь про трикутник у повсякденному житті. Щиро дякую за співпрацю на уроці! Бажаю успіхів у навчанні!