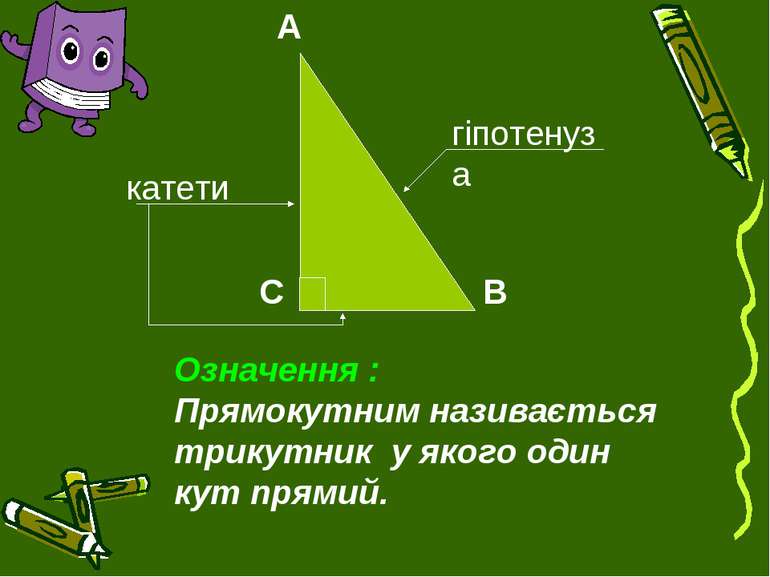
Презентація на тему:
РОЗВ’ЯЗУВАННЯПРЯМОКУТНИХТРИКУТНИКІВ

РОЗВ’ЯЗУВАННЯ ПРЯМОКУТНИХ ТРИКУТНИКІВ Підготувала: Голуб Наталія Андріївна Тальнівська загальноосвітня школа I-III ст.№2 Тальнівського району

Означення : Прямокутним називається трикутник у якого один кут прямий. катети гіпотенуза

Властивості прямокутного трикутника 1. Сума гострих кутів прямокутного трикутника дорівнює 90º. А+ В = 90º 2. Катет , який лежить проти кута 30º дорівнює половині гіпотенузи . Якщо А = 30º , то ВС = 0,5АВ

Теорема Піфагора У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів . АВ² =АС²+ВС²

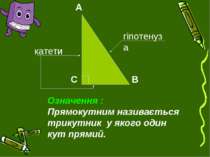
Означення Синусом гострого кута прямокутного трикутника називається відношення протилежного катета до гіпотенузи .

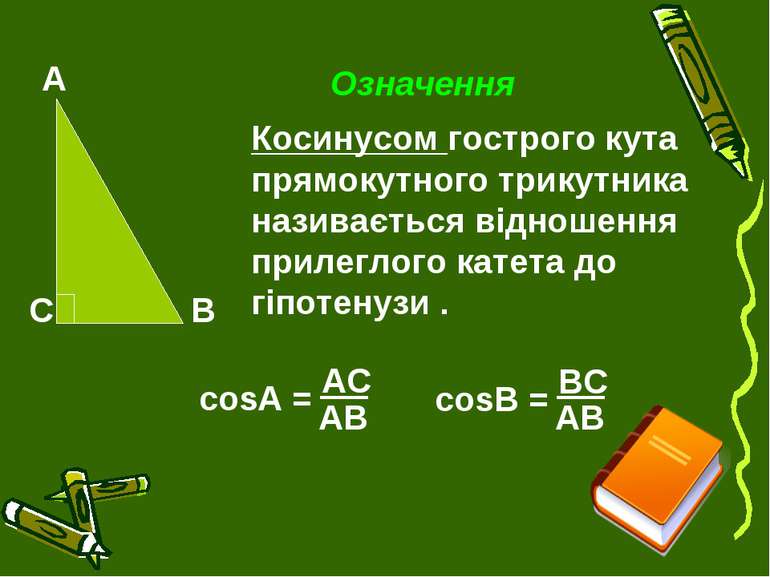
Означення Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи .

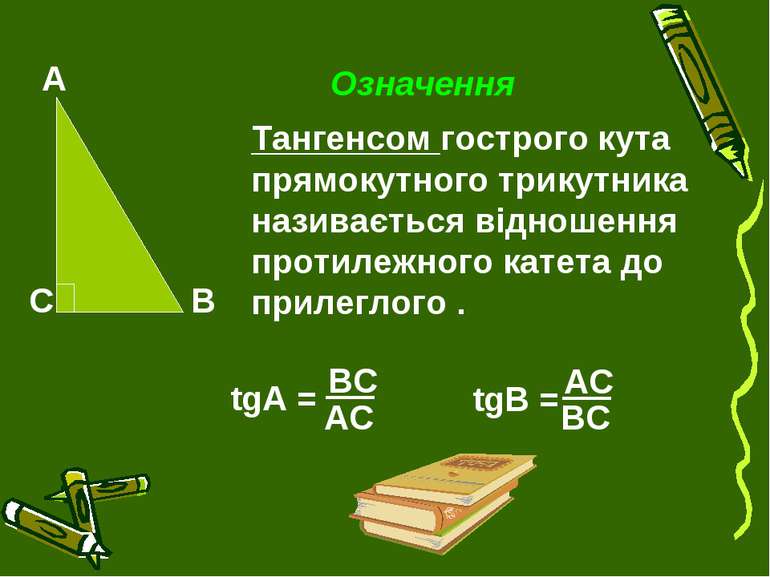
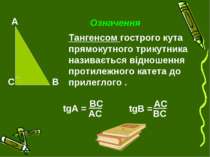
Означення Тангенсом гострого кута прямокутного трикутника називається відношення протилежного катета до прилеглого . tgА = tgB = АС ВС

Співвідношення між сторонами і кутами прямокутного трикутника Катет прямокутного трикутника дорівнює добутку: гіпотенузи на синус протилежного кута АС=АВsinB BC=ABsinA гіпотенузи на косинус прилеглого кута AC=ABcosA ВC=ABcosВ - другого катета на тангенс протилежного кута AC=BCtgB BC=ACtgA

Співвідношення між сторонами і кутами прямокутного трикутника Гіпотенуза прямокутного трикутника дорівнює частці від ділення : катета на синус протилежного кута АВ= АB= катета на косинус прилеглого кута AВ= АВ=

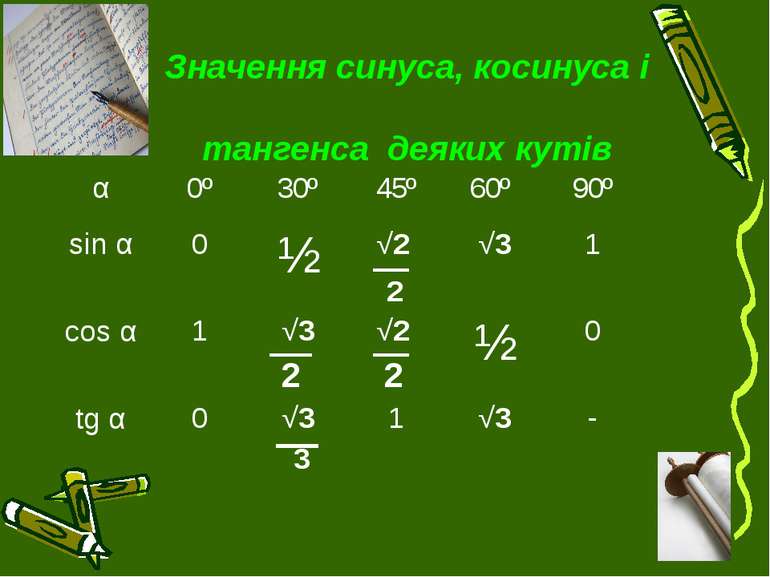
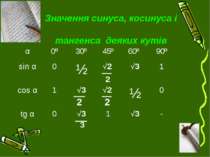
Значення синуса, косинуса і тангенса деяких кутів 2 2 2 α 0º 30º 45º 60º 90º sin α 0 ½ √2 √3 1 cos α 1 √3 √2 ½ 0 tg α 0 √3 3 1 √3 -

Перевір себе Який трикутник називається прямокутним? Сформулюйте теорему Піфагора. Сформулюйте властивості прямокутного трикутника. 4 Що називається синусом гострого кута прямокутного трикутника? 5 Як знайти катети за гіпотенузою і гострим кутом? 6 Як знайти гіпотенузу за катетами ?

Піфагор Самоський (580-500рр до н.е ) Давньогрецький філософ, вчений , математик. Зробив значний вклад в розвиток тогочасної науки. Відкрите ним правило знаходження величин сторін прямокутного трикут- ника, назване нині “теоремою Піфагора”, є головною і найкращою теоремою геометрії.

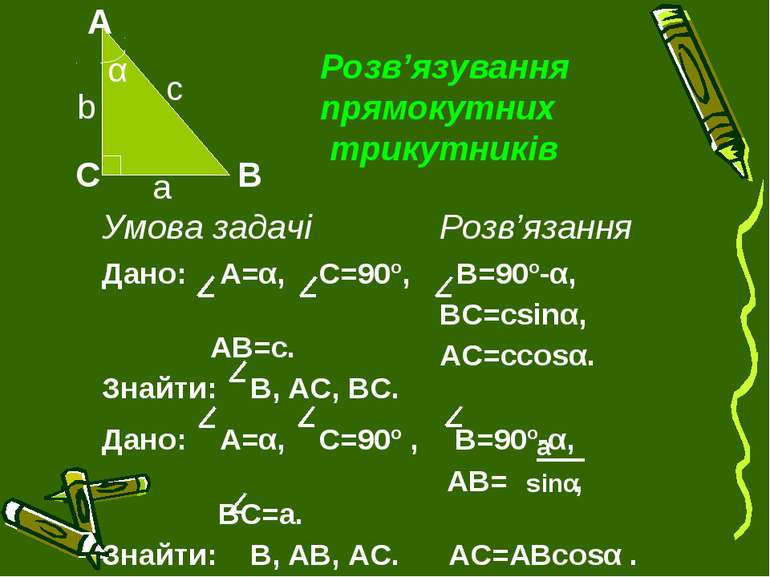
Розв’язування прямокутних трикутників а Умова задачі Розв’язання Дано: А=α, С=90º, АВ=с. Знайти: В, АС, ВС. В=90º-α, ВС=сsinα, АС=сcosα. Дано: А=α, С=90º , ВС=а. Знайти: В, АВ, АС. В=90º-α, АВ= , АС=АВcosα .

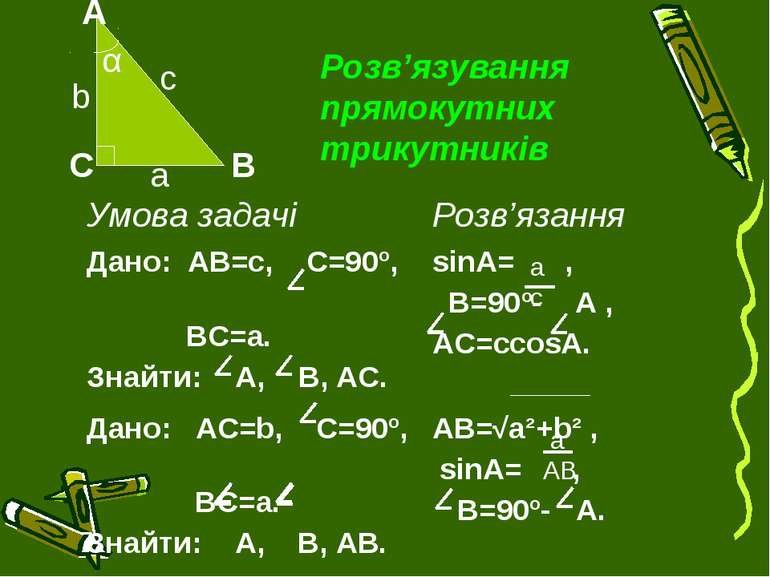
Розв’язування прямокутних трикутників а Умова задачі Розв’язання Дано: АВ=с, С=90º, ВС=а. Знайти: А, В, АС. sinА= , В=90º- А , АС=сcosА. Дано: АС=b, С=90º, ВС=а. Знайти: А, В, АВ. АВ=√а²+b² , sinА= , В=90º- А.

Розв’яжи самостійно Діагональ прямокутника дорівнює 85 см і утворює зі стороною кут 65º. Знайдіть сторони прямокутника. Задача 1 Задача 2 Катет і гіпотенуза прямокутного трикутника пропорційні числам 7 і 25. Знайдіть синус, косинус і тангенс гострих кутів трикутника.

Розв’язання задачі 1 ВВ З ACD ( D=90º). AD=ACsinC, CD=ACcosC. Дано: АС=85см, АСD=65º Знайти: AD, CD. Розв’язання. AD=85sin65º=85·0,906=77,01 CD=85cos65º=85·0,423=35,96 Відповідь: 77,01см, 35,96см.

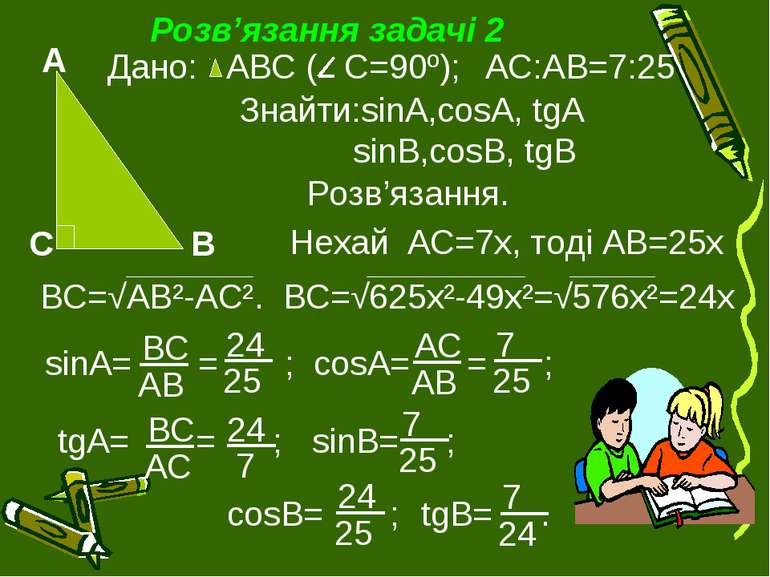
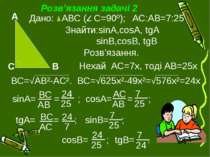
Розв’язання задачі 2 Дано: АВС ( С=90º); АС:АВ=7:25 Знайти:sinA,cosA, tgA sinB,cosB, tgB Розв’язання. Нехай АС=7х, тоді АВ=25х ВС=√АВ²-АС². ВС=√625х²-49х²=√576х²=24х sinA= = ; cosA= = ; tgA= = ; sinB= ; cosB= ; tgB= .

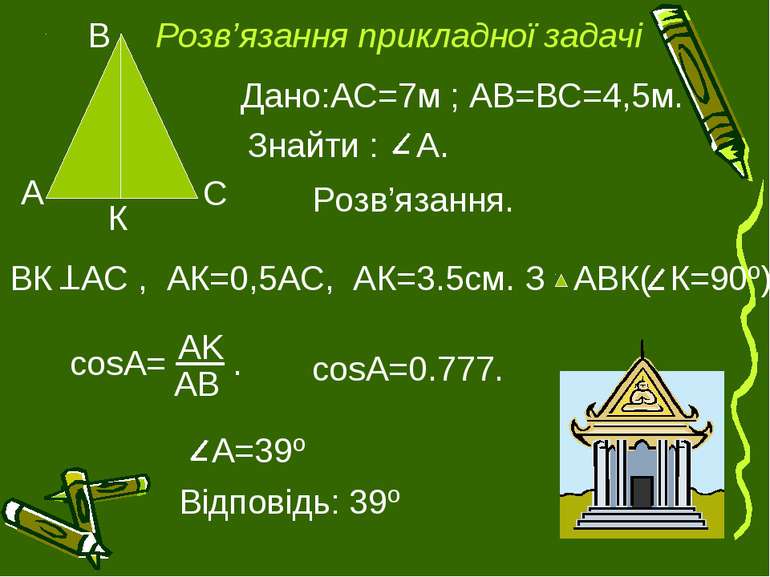
Прикладні задачі Задача 1 Ширина будинку 7 м, довжина крокви 4,5 м. Під яким кутом крокви нахилені до стелі ?

Розв’язання. Дано:АС=7м ; АВ=ВС=4,5м. Знайти : А. К ВК АС , АК=0,5АС, АК=3.5см. З АВК( К=90º) Τ Розв’язання прикладної задачі cosA= . cosA=0.777. А=39º Відповідь: 39º

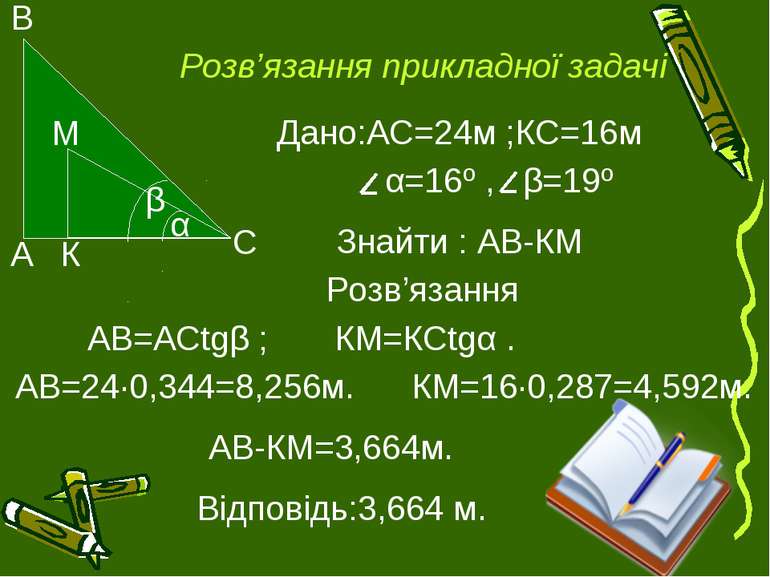
Задача 2 Вершину дерева, віддаленого від даного пункту на 16 м, видно під кутом 16º до горизонту , а вершину другого дерева віддаленого від цього самого пункту на 24 м, видно під кутом 19º. Яке дерево вище і на скільки?

Розв’язання прикладної задачі Дано:АС=24м ;КС=16м α=16º , β=19º Знайти : АВ-КМ Розв’язання АВ=АСtgβ ; КМ=КСtgα . АВ=24·0,344=8,256м. КМ=16·0,287=4,592м. АВ-КМ=3,664м. Відповідь:3,664 м.