Презентація на тему:
Розвязування задач на знаходження площі трикутника

Бутар Т.Б. вчителя математики Черкаської гімназії № 31 Черкаської міської ради

Теорема синусів

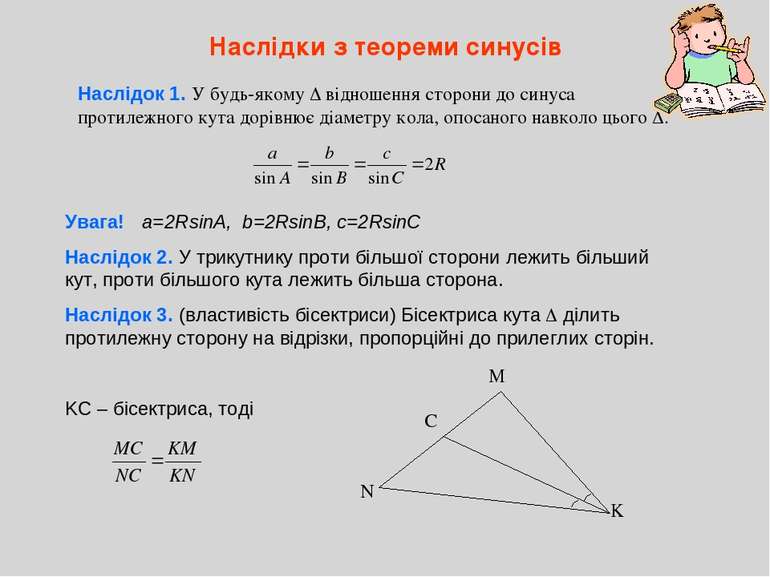
Наслідки з теореми синусів Наслідок 1. У будь-якому відношення сторони до синуса протилежного кута дорівнює діаметру кола, опосаного навколо цього . Увага! а=2RsinA, b=2RsinB, c=2RsinC Наслідок 2. У трикутнику проти більшої сторони лежить більший кут, проти більшого кута лежить більша сторона. Наслідок 3. (властивість бісектриси) Бісектриса кута ділить протилежну сторону на відрізки, пропорційні до прилеглих сторін. KC – бісектриса, тоді

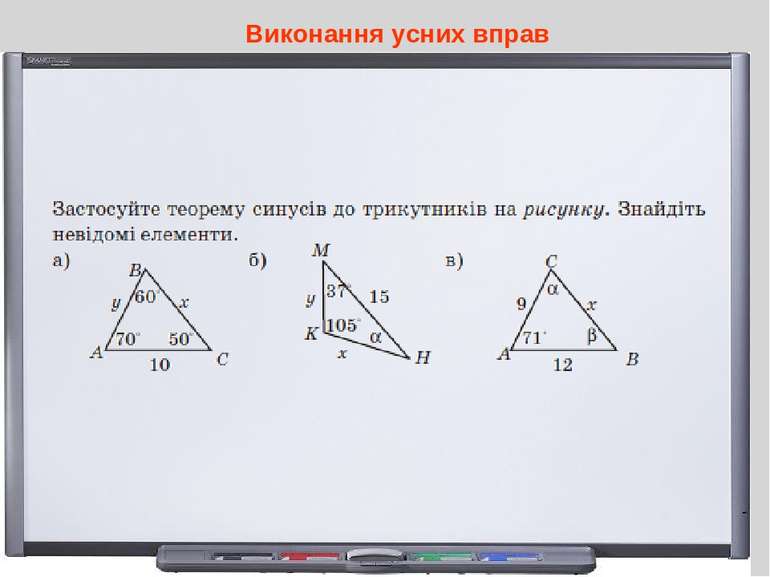
Які типи задач можна розв’язати за допомогою теореми синусів? За стороною і прилеглими до неї кутами знаходити інші сторони і кути трикутника. За двома сторонами і кутом, протилежним до однієї з них, знаходити інші сторони і кути трикутника. За стороною і протилежним кутом знаходити радіус кола, описаного навколо цього трикутника.

Виконання усних вправ

Приклад. У трикутнику ABC дано b = 9см, с = 11 см, B = 50°. Знайти С, A. Дано: АВС ( див рис.), АС = 9 см, АВ = 11 см, B = 50°. Знайти: A, C. Розв'язання За теоремою синусів Цьому значенню синуса відповідає два кути 69° і 111°. Тоді A = 180° - ( C + B), A = 180°- (50° + 69°) = 61° або A =180°-(50° + 111°)= 19°. Відповідь. 69°, 61° або 111°, 19°. Звідси Виконання вправ

Виконання вправ Приклад. У прямокутному трикутнику бісектриса гострого кута ділить протилежний катет на відрізки завдовжки 8 см і 10 см. Знайти гіпотенузу трикутника. Дано: АВС - прямокутний ( C= 90°) СК= 8 см, ВК= 10 см. Знайти: АВ. Розв 'язання За властивістю бісектриси СК:ВК = АС: АВ = 8 : 10 = 4 : 5 . Отже, АС становить 4 частини, АВ - 5 таких частин. Нехай одна частина дорівнює х см, тоді АС = 4х см, АВ = 5х см. СВ = 8 + 10 = 18 (см). За теоремою Піфагора АВ2 = АС2 + СВ2. Маємо: (4х)2 + 182 = (5х)2; 16х2 + 324 = 25х2; 9х2 = 324, х2 = 36, х = ±6, -6 — не задовольняє умову задачі. Отже, х = 6, тоді АВ = 5 · 6 = 30 (см). Відповідь. 30 см.

Використані джерела http://vmesteosa.blogspot.com/ Геометрія: підруч. для 9 кл. загальноосвіт. навч. закладів / А.Г. Мерзляк, В.Б. Полянський, М.С. Якір. – Х.: Гімназія, 2017. -240 с. : іл. Олійник Л.І., Геометричний тренажер. 9 клас.- Тернопіль: Підручники і посібники, 2011.-160с.