Презентація на тему:
Площі фігур

Площі фігур Дидактичний матеріал до уроку геометрії з досвіду роботи вчителя математики Снов“янської ЗОШ І – ІІ ст Чернігівського району Чернігівської області Колько Н.М.

Геометрія - це наука про властивості фігур Геометрія – слово грецьке, означає «землемірство»

З давніх часів обчислювання площ було одним з найважливіших застосувань геометрії. У Стародавньому Єгипті заплави річки Нілу землероби почали обробляти приблизно в п’ятому тисячолітті до н.е. Тоді і виникла потреба в обчисленні площ. На підставі документів, що дійшли до нас, вже у Х Υ – ХΥІ ст. до н.е. єгиптяни вміли вимірювати площі прямокутника, трикутника і трапеції за відомими тепер правилами. Обчислення площі або поверхні фігури називається « квадратурою», що в перекладі з латинської означає надання квадратної форми. У стародавніх єгиптян квадратура якоїсь фігури зводилася до побудови квадрата, що мав таку саму площу. Звідси зрозуміле походження слова «квадратура».

Поняття площі

Плоским трикутником називають скінченну частину площини, обмежену трикутником

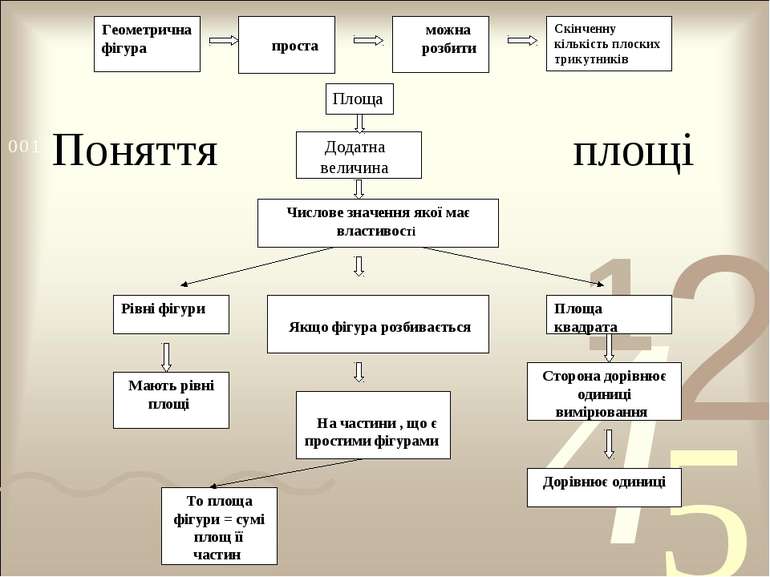
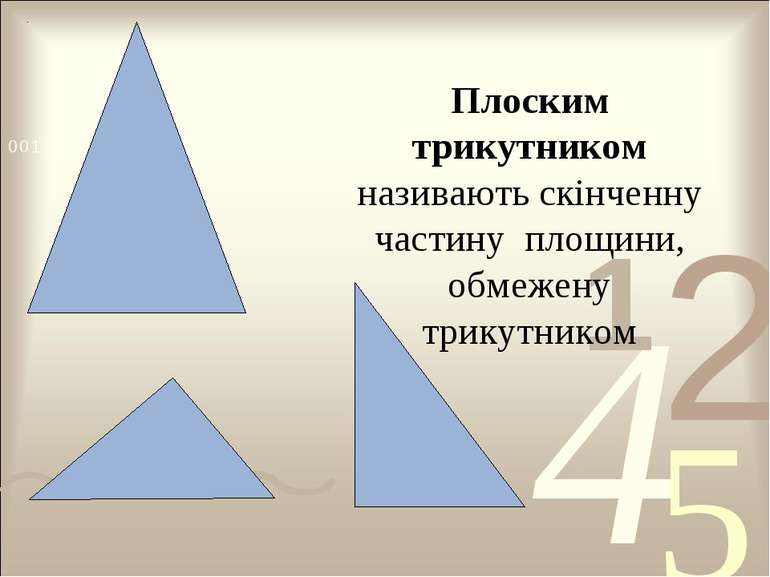
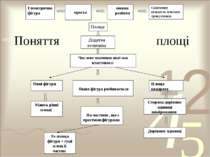
Геометричну фігуру називатимемо простою, якщо її можна розбити на скінченну кількість плоских трикутників.

Площа – це додатна величина, числове значення якої має такі властивості: рівні фігури мають рівні площі; якщо фігура розбивається на частини, що є простими фігурами, то площа цієї фігури дорівнює сумі площ її частин; площа квадрата зі стороною, що дорівнює одиниці вимірювання, дорівнює одиниці.

За одиницю вимірювання площ приймають площу квадрата, сторона якого дорівнює одиниці вимірювання відрізків.

1 мм 2– площа квадрата зі стороною 1 мм 1 см 2 – площа квадрата зі стороною 1 см 1 дм 2– площа квадрата зі стороною 1 дм 1 м 2 – площа квадрата зі стороною 1 м 1 ар - площа квадрата зі стороною 10 м, 1 гектар – площа квадрата зі стороною 100м

Квадрат

Прямокутник

Паралелограм

Чотирикутник

Ромб від грецького «ромбос» - бубон ( у стародавні часи цей ударний музичний інструмент мав форму ромба).

Трапеція

Трикутник

Трикутник

Герон Александрійський ( мабуть І ст. н.е.) – давньогрецький математик – енциклопедист, який працював в Александрії. Праці його мали головним чином прикладний характер. Він був видатним механіком, його навіть називали « Герон – механік». У творах « Пневматика» і «Механіка» описав автомат для відкривання дверей, автомат для продажу «священної води», пожежний насос тощо. Багато уваги Герон приділяв питанням геодезії і практичному застосуванню геометрії. У кращій з математичних праць «Метрика», він виклав практичні правила для обчислення площ та об’ємів геометричних фігур, які застосовували давньогрецькі, римські та середньовічні землеміри і техніки.

Формула Герона красива, симетрична, зручна, легко запам’ятовується, справжня формула – красуня! Цікава й історія її творення. Називають її ім'ям Герона Олександрійського (Старшого) не зовсім заслужено, бо вперше відкрив і обґрунтував її Архімед. А Герон тільки через чверть тисячоліття після того вмістив її у своїй праці «Метрика». Тому справедливіше було б називати її формулою Архімеда або принаймні Архімеда – Герона. Отже, про формулу Герона можна було б написати цілу поему. Формула Герона досить корисна, бо за її допомогою можна розв’язувати багато цікавих і важливих задач. І все таки користуватися нею бажано тільки тоді, коли вона справді доцільна.

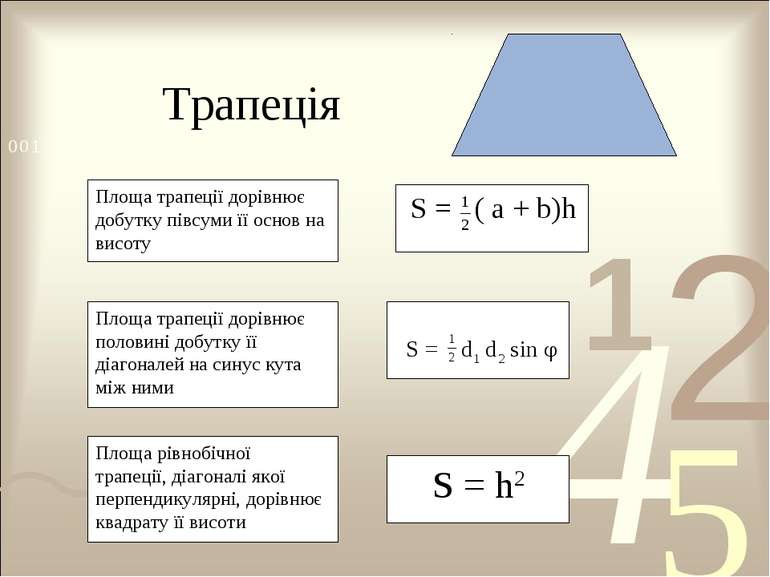
Задача Знайти площу трапеції, у якої паралельні сторони 20 см і 60 см, а непаралельні – 13 см і 37 см

І спосіб За формулою Герона S KCD = 240 (см 2) S KCD = KD· CN, KD = 60 – 20 = 40 (см), CN = 12 (см) За формулою площі трапеції S =( 60+20) : 2 · 12 = 480 (см2). Відповідь: S = 480 (см2).

ІІ спосіб З трикутника CKD за теоремою косинусів CD2 = CK2 + KD2 – 2 CK · KD cos < CKD знайдемо cos < CKD = cos α і sin α. тоді CN = CK sin α. CN =12 (см). За формулою S =( 60+20) : 2 · 12 = 480 (см2). Відповідь: S = 480 (см2).

ІІІ спосіб Нехай КN = х, тоді ND = 40 – х. Для ∆ CKN і ∆ CND застосуємо теорему Піфагора і знайдемо CN : CN 2 = 132 – х2, CN2 = 372 – (40 -х)2 . З рівняння 132 – х2 = 372 – (40 -х) 2 х = 5, CN =12 (см) . За формулою S =( 60+20) : 2 · 12 = 480 (см2). Відповідь: S = 480 (см2).

ІУ спосіб Продовжимо АВ і СD до перетину в т. О. ∆АОD ˜ ∆ВОС (за кутами ). Тоді OD =1,5 ∙ 37 = 55,5 (см), ОА =1,5 ∙13 = 19,5 (см). За формулою Герона знайдемо SAOD = 540 (см2). SABCD = SAOD. SABCD =480 (см2). Відповідь: S = 480 (см2).

Задача Один веселий кулінар зробив торт у вигляді правильного шестикутника АВСDFG . Після цього він перетворив його у круглий торт, з’ївши залишки. Поміркувавши, він вирішив, що попередня форма торта була кращою, і , знову з’ївши залишки, отримав нарешті правильний шестикутник LMNOPR . Яку частину початкового торта з’їв кулінар?

Вчитись можна тільки весело. Щоб перетравити знання, треба поглинати їх з апетитом! Анатоль Франс