Презентація на тему:
Нерівності трикутників

Нерівності трикутників Геометрія 7 клас

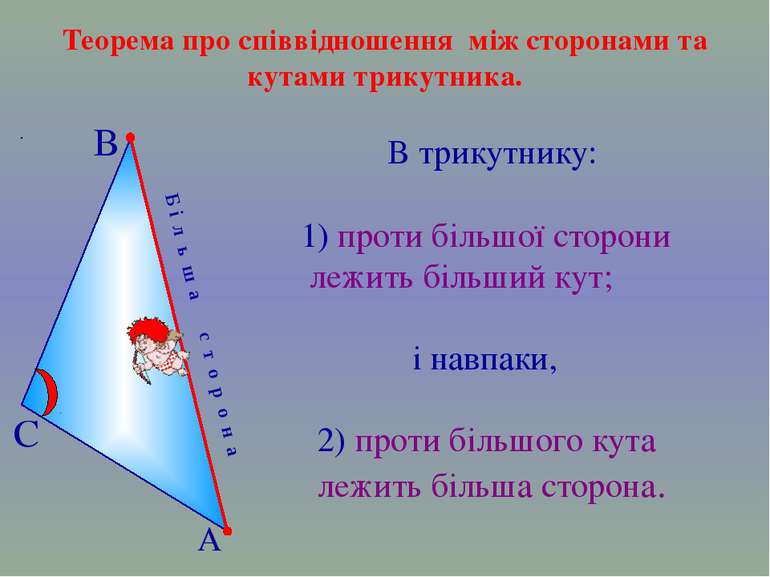
Б і л ь ш а с т о р о н а В трикутнику: 1) проти більшої сторони лежить більший кут; і навпаки, 2) проти більшого кута лежить більша сторона. А В С Теорема про співвідношення між сторонами та кутами трикутника.

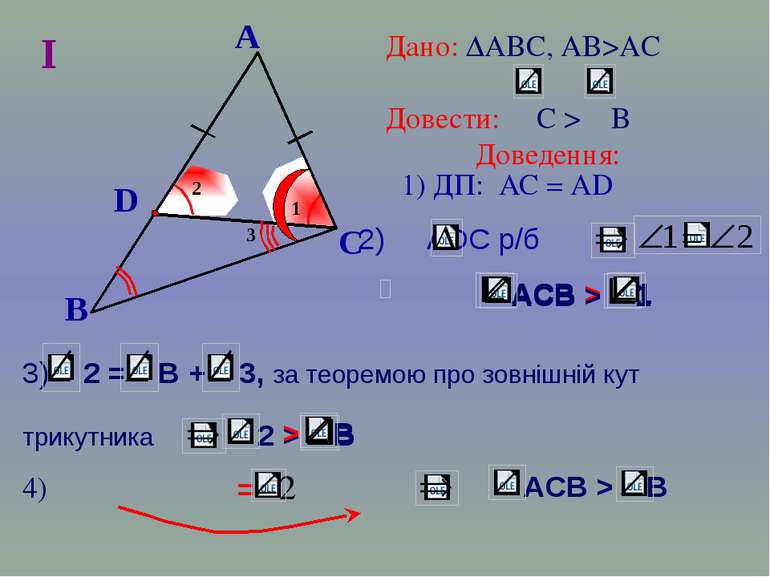
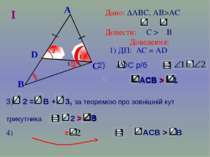
B A C Дано: ∆АВС, АВ>AC Довести: С > B Доведення: 1) ДП: АС = АD 4) = 2 I АCВ > 1 3 D 2) АDС р/б 3) 2 = В + 3, за теоремою про зовнішній кут трикутника 2 > B АCВ > 1 > B

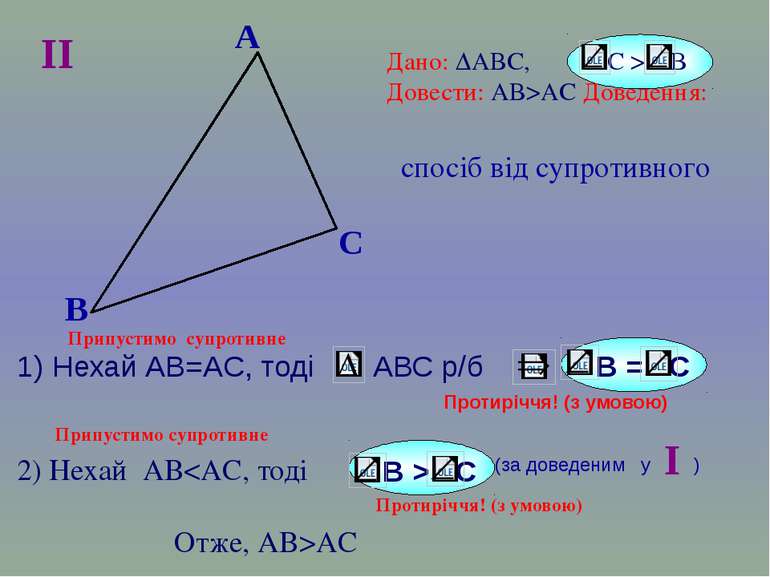
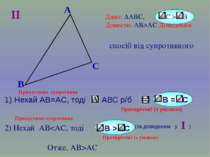
B A C Дано: ∆АВС, С > B Довести: АВ>AC Доведення: спосіб від супротивного II Протиріччя! (з умовою) 2) Нехай АВAC Припустимо супротивне Припустимо супротивне В = С 1) Нехай АВ=AC, тоді АВС р/б В > С I (за доведеним у )

Нерівності трикутників Кожна сторона трикутника менша від суми двох інших його сторін.

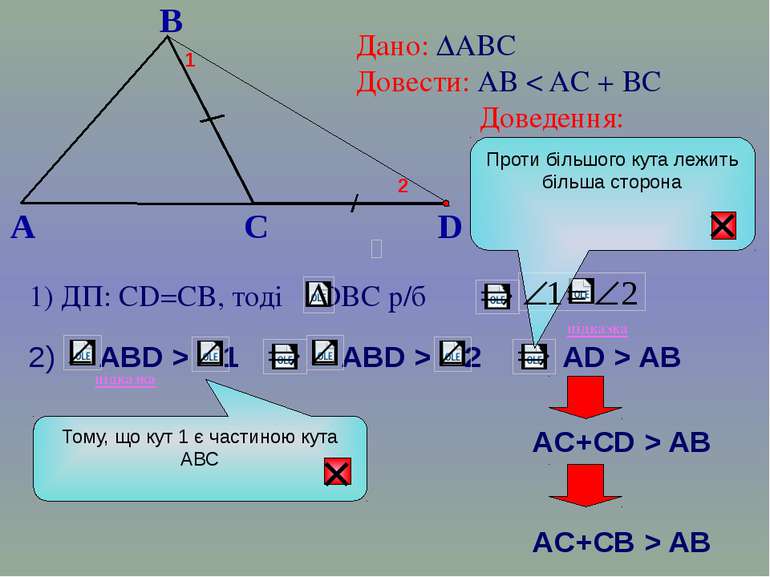
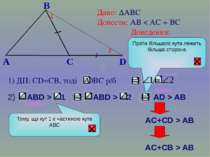
B A C Дано: ∆АВС Довести: АВ < AC + BC Доведення: 1) ДП: СD=CB, тоді DВС р/б підказка підказка D 1 2 2) АD > AB АC+CD > AB АC+CВ > AB Тому, що кут 1 є частиною кута АВС Проти більшого кута лежить більша сторона

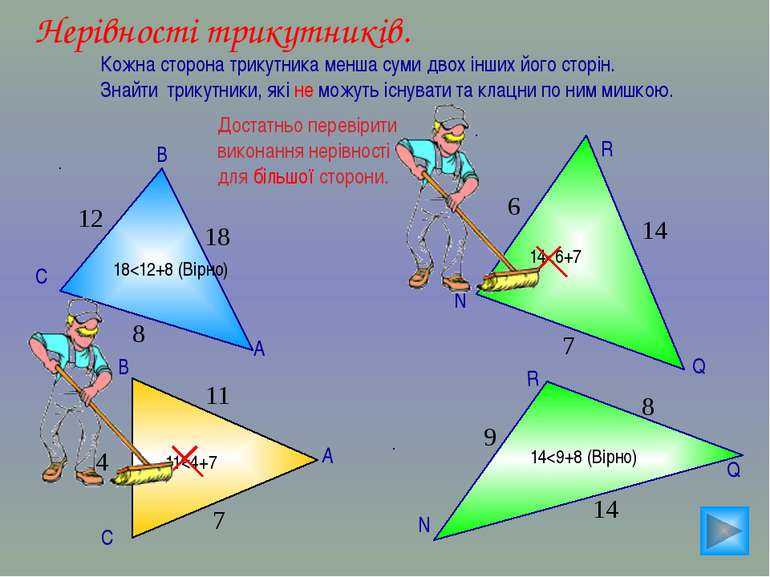
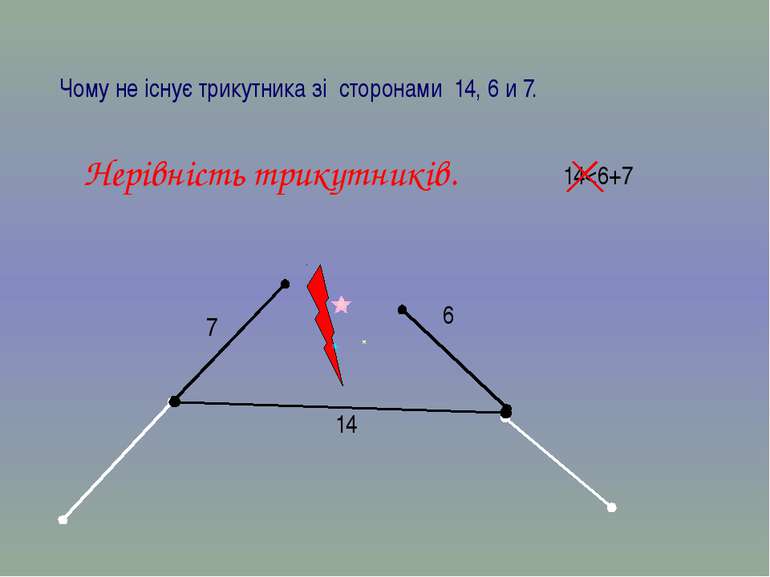
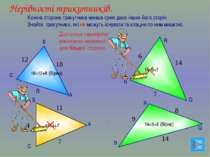
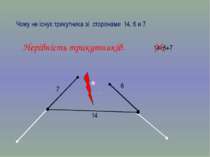
Нерівності трикутників. Кожна сторона трикутника менша суми двох інших його сторін. Знайти трикутники, які не можуть існувати та клацни по ним мишкою. Q R N 8 9 14 18

Чому не існує трикутника зі сторонами 14, 6 и 7. 14 6 7 14

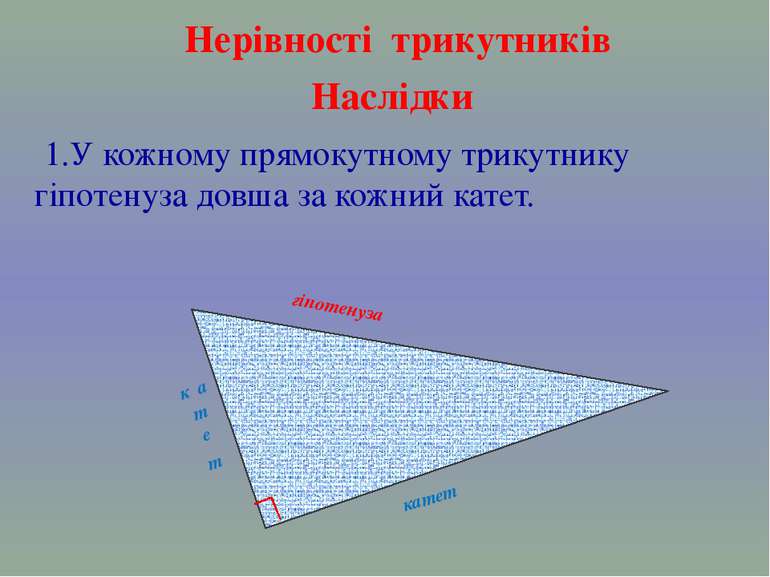
Нерівності трикутників Наслідки 1.У кожному прямокутному трикутнику гіпотенуза довша за кожний катет. к а т е т гіпотенуза катет

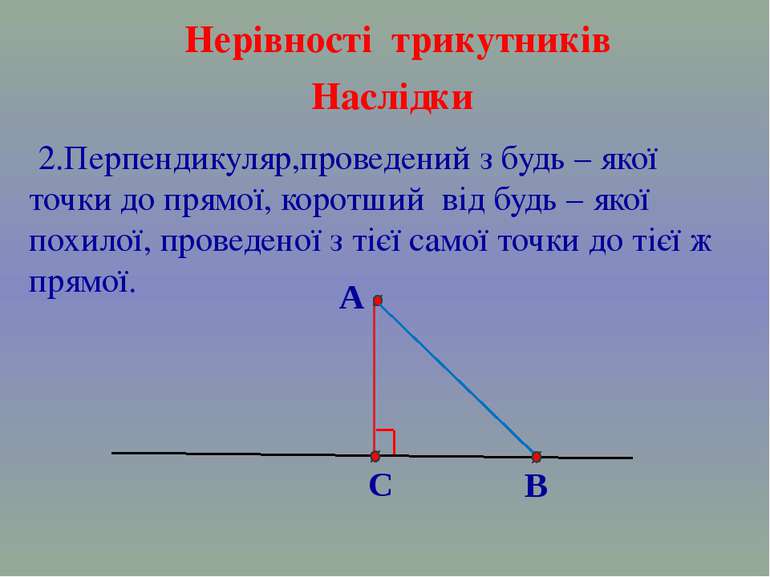
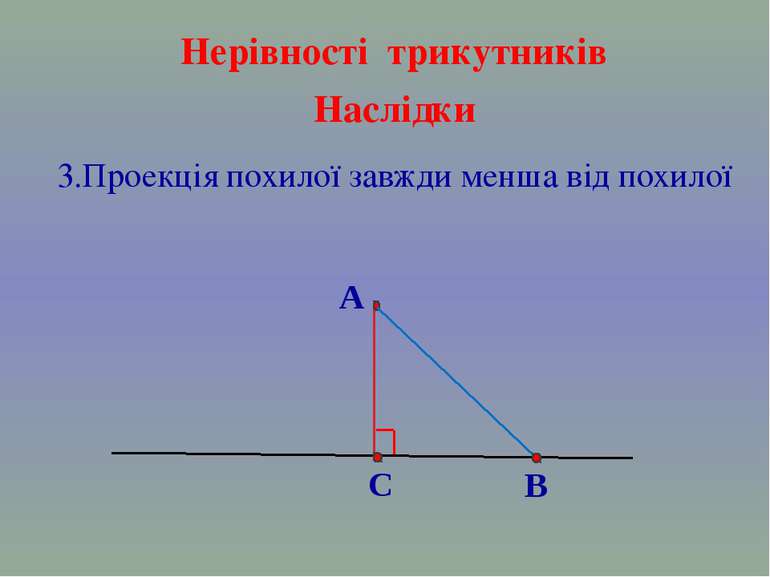
2.Перпендикуляр,проведений з будь – якої точки до прямої, коротший від будь – якої похилої, проведеної з тієї самої точки до тієї ж прямої. Нерівності трикутників Наслідки C А В

3.Проекція похилої завжди менша від похилої Нерівності трикутників Наслідки А C В