Презентація на тему:
Геометрія. Історія та основи

Дана презентація підготовлена в цілях здачі практичної роботи, так і в інших, як-от використання по призначенню. Я не проти. Справді.

Beta version

Означення Геометрія (грецьке слово, яке означає землемірство; geo – Земля, metreo – міряю) – розділ математики, що вивчає просторові відношення (наприклад, взаємне розташування) і форми (наприклад, геометричні тіла) та їх узагальнення.

З просторовими формами людина зустрічалася насамперед при вимірюванні ділянок землі. Традиційно вважається, що родоначальниками геометрії є стародавні греки, які перейняли у єгиптян ремесло землемірства і вимірювання об'ємів тіл, а згодом перетворили її на науку. Геометрія греків, звана сьогодні евклідовою, або елементарною, займалася вивченням простих форм: прямих, площин, відрізків, правильних багатокутників і многогранників, конічних перетинів, а також куль, циліндрів, призм, пірамід і конусів. Обчислювалися їх площі і об'єми. Перетворення в основному обмежувалися подібністю. В стародавній Греції, починаючи з 7 ст. до н.е. з часів Фалеса Мілетського починається новий етап розвитку геометрії. Вона набуває характерного для неї абстрактного напряму. Виникає доведення. Саме стародавня Греція дала світу строгу побудову геометрії як системи пропозицій (теорем), основні поняття, що послідовно виводяться з нечисленних визначень, та істин, приймаються без доказу (аксіом). Такий виклад геометрії в «Початках» Евкліда (близько 300 до н. е.) в перебіг майже 2 тисяч років служив зразком застосування аксіоматичного методу і основної побудови евклідової геометрії.

Якби спитати будь-якого з істориків математики, кого з старогрецьких математиків він вважає найвидатнішим, причому дозволяється називати не більше трьох імен, то, мабуть, у більшості випадків відповідь була б така: Евклід, Архімед, Аполлоній. Це справді три кити стародавньої математики, і ніяка, навіть найкоротша, довідка про стародавній світ і його науку неможлива без згадування цих трьох імен. Евклід – є фокусом, в якому сконцентрувалася уся сучасна математика. Архімед – геніальний механік і геометр, творець нескінченно малих величин (числення). Апполоній – творець теорії конічних перерізів. Середні віка небагато дали геометрії, і наступною великою подією в її історії стало відкриття Декартом в XVII столітті координатного методу («Міркування про метод», 1637 р.). Рене Декарт запропонував метод координат, який дозволив пов'язати геометрію з алгеброю і математичним аналізом, що породило аналітичну геометрію і диференціальну геометрію. Точкам зіставляються набори чисел, це дозволяє вивчати відносини між формами методами алгебри. Так з'явилася аналітична геометрія, що вивчає фігури і перетворення, які в координатах задаються рівняннями алгебри. Приблизно одночасно з цим Паскалем і Дезаргом почато дослідження властивостей плоских фігур, не змінних при проектуванні з однієї площини на іншу. Цей розділ отримав назву проектної геометрії. Метод координат лежить в основі диференціальної геометрії, де фігури і перетворення все ще задаються в координатах, але вже довільними достатньо гладкими функціями.

У 1826 році Н. І. Лобачевський побудував геометрію Лобачевського. Лобачевського геометрія – це геометрична теорія, заснована на тих же основних постулатах, що і звичайна евклідова геометрія, за винятком аксіоми про паралельність. Евклідова аксіома говорить: на площині через точку, яка не лежить на даній прямій, можна провести одну і тільки одну пряму, паралельну даній. У геометрії Лобачевського ця аксіома замінена наступною: на площині через точку, яка не лежить на даній прямій, можна провести більше однієї прямої, яка не перетинатиме дану пряму. Не дивлячись на зовнішню парадоксальність, геометрія Лобачевського виявилася логічно абсолютно рівноправною з евклідовою. Відкриття неевклідової геометрії Лобачевського внесло корінні зміни до уявлень про природу простору. В середині 19 ст. були розглянуті багатовимірні простори. Деякий загальний принцип побудови різних узагальнених понять простору (і відповідної ним геометрії) на основі теорії груп перетворень був даний Ф. Клейном (1872). Обширна область геометрії – ріманова геометрія – була закладена в другій половині 19 століття в роботах Б. Рімана. Узагальнення основного предмету геометрії – простори – привело до плідного застосування геометрії в різних областях не тільки математики, але й інших наук (фізики, механіки).

Елементарною геометрією називають геометрію, яка вивчає найпростіші геометричні властивості об’єктів тривимірного простору, тобто простору, в якому ми з вами живемо. Первинні поняття — це такі найпростіші поняття в математиці, які не можна визначити через поняття ще більш прості. Чітке уявлення про точки дають перетини ліній між собою і ліній з поверхнями. Точка не має жодного виміру. Уявлення про геометричне тіло дає нам будь-який предмет, якщо розглядати лише його форму і розміри. Геометричне тіло має три виміри. Поверхню можна уявити собі, як спільну частину двох суміжних (прилеглих) областей простору, або як нескінченно тонкий шар, який відокремлює дві суміжні частини простору один від одного. Поверхня не має товщини. Лінія представляється як спільна частина (границя) двох суміжних ділянок поверхні. В результаті перетину двох поверхонь ми одержуємо лінію. Лінія має лише один вимір — довжину. Точка відокремлює одну від другої суміжні частини лінії. Точки позначаються великими буквами латинського алфавіту. Наприклад, точка B.

Площина — окремий вид поверхні, будь-яка частина якої може бути суміщена (поєднана; сполучена) з вихідною площиною в будь-якому її місці як у прямому, так і в перевернутому вигляді (властивість прямого і перевернутого ковзання). Площини позначаються малими буквами грецького алфавіту. Наприклад, площина α чи γ, тощо. Якщо через дві точки площини провести пряму лінію, то і всі точки цієї прямої будуть знаходитися на площині. Пряма лінія є окремим видом лінії. Наочне уявлення про пряму лінію дає перетин двох площин. Прямі позначаються малими або двома великими буквами латинського алфавіту. Наприклад, пряма AB.

Властивості прямої: Через будь-які дві точки простору можна провести пряму і до того ж тільки одну. Якщо дві прямі накладені одна на одну так, що які-небудь дві точки однієї прямої збігаються з двома точками другої прямої, то ці прямі збігаються і в усіх інших точках. Дві прямі можуть перетинатися лише в одній точці. Пряма має властивість ковзання — будь-яка її ділянка може ковзати по обидві сторони прямої нескінченно. Таку саму властивість має ще тільки одна лінія — коло. Проте властивості, 1-3 для кола (повністю або частково) не виконуються: через будь-які дві точки простору можна провести нескінченне число кіл; два кола можуть мати дві спільні точки, але не збігатися в усіх інших точках, два кола можуть стикатися в одній точці або перетинатися в двох точках.

Нескінченна пряма — пряма, яка продовжується в обидві сторони нескінченно. Звичайно нескінченну пряму називають просто «пряма». Відрізок прямої — частина прямої, обмежена з двох сторін точками. Точками самоперетину ламаної лінії називаються такі точки, в яких перетинаються її ланки. Кінці ланок при цьому не враховуються. Промінь або півпряма — частина прямої, обмежена лише з однієї сторони, тобто промінь є частиною прямої, яка виходить із заданої точки і прямує до нескінченності в даному напрямку. Ламана лінія — лінія, утворена відрізками прямих, що не лежать на одній прямій і розміщені так, що кінець першого відрізка є початком другого, кінець другого — початком третього і т. д. Відрізки прямих, що утворюють ламану, називаються сторонами (ланками) ламаної. Точки стику відрізків називаються вершинами ламаної. Ламана лінія називається опуклою, якщо всі її ланки розміщені по одну сторону від кожного відрізка, що входить до її складу, і продовженого необмежено в обидва кінці. Ламана називається замкненою, якщо кінці її збігаються в одній точці.

Відрізок — частина прямої, що складається з усіх точок цієї прямої, котрі лежать між двома даними точками, які називаються кінцями відрізка. Відрізок позначається двома великими латинськими літерами, що відповідають кінцям відрізка.

Два відрізки вважаються рівними, якщо вони можуть бути суміщені своїми кінцями. Якщо на даному відрізку взяти дві точки, з яких хоча б одна не збігається з кінцем даного відрізка, то відрізок, обмежений цими точками, називається частиною даного відрізка. Якщо один відрізок дорівнює частині другого, то про ці відрізки кажуть, що перший є меншим, від другого, а другий — більшим від першого. Відрізок вважається орієнтованим, якщо домовилися про те, де його початок і кінець.

Додаванням (відніманням) відрізків називається графічна операція, за допомогою якої на деякій прямій можна побудувати відрізок, який є сумою даних відрізків — доданків (або відрізок — різниця відрізків зменшуваного і від’ємника). Додавання відрізків слід відрізняти від додавання довжин відрізків. Сумою двох або декількох відрізків називається відрізок, побудований на деякій прямій за даними відрізками без їх взаємного накладання, і без проміжків між ними. Сума відрізків має переставну і сполучну властивості. Різницею двох відрізків називається такий третій відрізок, який в сумі з меншим відрізком дорівнює більшому відрізку.

Помножити відрізок на ціле додатне число n — значить знайти суму n таких відрізків. Одержаний в результаті відрізок буде відрізком — добутком. Поділити відрізок на ціле додатне число n — значить знайти такий відрізок, після множення якого на число n одержимо даний відрізок. Помножити відрізок на додатний раціональний дріб m/n — значить помножити цей відрізок на число m і одержаний відрізок поділити на n частин. Можна також виконати спочатку ділення на n, а потім множення на m. Для швидкої побудови відрізків виду a • m/n за даним відрізком a існує спеціальний прилад — пропорціональний (подільний) циркуль. Цей прилад складається з двох рівних за довжиною ніжок з прорізами, які дають можливість змінювати довжину ніжок, коли ослаблено скріплюючий гвинт Відношення віддалі між вістрями верхніх ніжок до віддалі між вістрями нижніх ніжок дорівнює відношенню довжини верхніх ніжок до довжини нижніх ніжок. Тому, установивши за шкалою гвинт так, щоб довжини верхніх і нижніх ніжок знаходилися в даному відношенні і вимірявши нижніми ніжками даний відрізок, одержуємо шуканий відрізок як віддаль між кінцями верхніх ніжок. Для швидкої побудови відрізків виду a • m/n за даним відрізком a існує спеціальний прилад — пропорціональний (подільний) циркуль. Цей прилад складається з двох рівних за довжиною ніжок з прорізами, які дають можливість змінювати довжину ніжок, коли ослаблено скріплюючий гвинт

Відношення віддалі між вістрями верхніх ніжок до віддалі між вістрями нижніх ніжок дорівнює відношенню довжини верхніх ніжок до довжини нижніх ніжок. Тому, установивши за шкалою гвинт так, щоб довжини верхніх і нижніх ніжок знаходилися в даному відношенні і вимірявши нижніми ніжками даний відрізок, одержуємо шуканий відрізок як віддаль між кінцями верхніх ніжок. Особливо зручно користуватися пропорціональним циркулем, коли необхідно змінювати в одному і тому самому відношенні велику кількість відрізків.

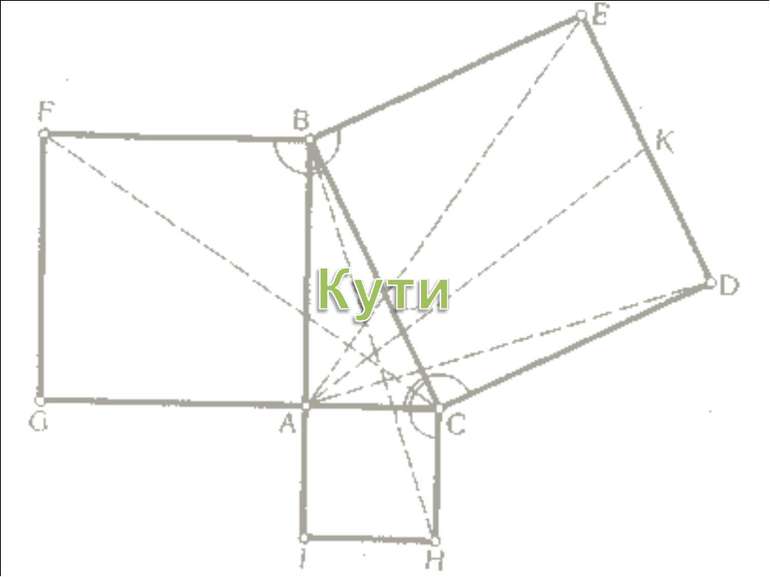
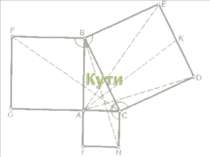
Плоский кут — фігура, утворена двома променями або відрізками, що виходять з однієї точки. Промені або відрізки, що утворюють кут, називаються сторонами кута, а точка, з якої вони виходять, вершиною кута. Кут позначається спеціальним значком і буквою, поставленою біля його вершини або всередині кута, а також трьома буквами, з яких середньою є та, що стоїть біля вершини кута. Наприклад, ∠A, ∠α, ∠POQ і т. д. Площина поділяється сторонами кута на внутрішню область кута і зовнішню. Два кути називаються рівними, якщо при накладанні вони збігаються. Розгорнутим кутом називається кут, одна сторона якого є продовженням іншої. Два кути, що мають спільну вершину і спільну сторону, називаються прилеглими, якщо їх внутрішні області не покривають одна одну. Якщо сторони кутів утворені відрізками, то при рівності кутів рівність сторін може не зберігатися.

Суміжними кутами називаються два прилеглих кути, у яких сторони, які не збігаються, утворюють пряму лінію. Щоб побудувати кут, суміжний даному, треба одну з сторін даного кута продовжити за його вершину. Якщо два суміжних кути рівні між собою, то кожний з них називається прямим кутом. Перпендикулярні прямі — такі дві прямі лінії, які при перетині утворюють прямі вертикальні або прямі суміжні кути. Вертикальні кути — такі два кути, у яких сторони одного є продовженням сторін другого. Вертикальні кути утворюються при перетині двох прямих ліній.

Якщо вершину і сторону одного кута сумістити з вершиною і стороною другого кута, а інші сторони цих кутів розмістити, по одну сторону від суміщеної, то: перший кут менший від другого, якщо несуміщена сторона його знаходиться всередині (у внутрішній області) другого кута; перший кут більший від другого, якщо несуміщена сторона його знаходиться у зовнішній області другого кута. Якщо вершину і сторону одного кута сумістити з вершиною і стороною другого кута так, щоб їх внутрішні області не накладалися, то утворений несуміщеними сторонами кут називається сумою даних кутів . Сума декількох кутів визначається аналогічно. Сума кутів має переставну і сполучну властивості. Різниця кутів, множення і ділення кута на число визначається аналогічно відповідним поняттям для відрізків. Бісектриса кута — промінь, що виходить з вершини кута і ділить кут на дві рівні частини (пополам). Бісектриси суміжних кутів взаємно перпендикулярні. Бісектриси вертикальних кутів становлять продовження одна одної.

Сидів і мучився над даною презентацією я – той, хто це написав. Тобто Кешишев Дімітр, от. Якщо Ви хочете прочитати про цього автора побільше, можете зайти на http://vkontakte.ru/id31693635

На момент 9 березня 2010 року, цей хлопець: Має 17 з хвостом років, бо родився 15 вересня 1992 року одного прохолодного ранку у вівторок; Учень 11-В класу Хмельницької СЗОШ №18; Слухає такі жанри музики, як Black metal, Death metal, Dark Ambient, Grindcore і трохи іншого (Thrash Metal, Noisecore, Deathcore, Crust punk, Sludge/Doom Metal, Drone Doom Metal); Патлатий; І щось інше. Говорю же – зайдіть у мої Вконтактики, і буде Вам добро.

Не забувайте, що дана презентація знаходиться в стадії бета-версії. Тобто, може бути доповнена інформацією та моєю уявою. А вона різною буває