Презентація на тему:
Визначення об'єму многогранників

Тема1. ОБ’ЄМ МНОГОГРАННИКІВ З історії розвитку поняття об’му геометричних тіл. Об’єм тіла. Основні властивості об'ємів. Об'єм прямокутного паралелепіпеда, призми. Об'єм похилого паралелепіпеда, похилої призми. Розв'язування задач. Об'єм піраміди. Об'єм зрізаної піраміди. Розв'язування задач. Многогранники в житті і практиці людини (Єгипетські піраміди, архітектурні споруди, побутові предмети).

З історії розвитку поняття об’єму геометричних тіл. Наприклад в Англії: 36,4 дм3 – бушель; 159 дм3 – барель; 12 дм3 – відро; 490 дм3 – діжка. Деякі з перелічених одиниць вимірювання використовуються і досі. У давнину деякі міри маси і об'єму часто збігалися з мірами вартості товару – грошовими одиницями. Зокрема, на Русі основна одиниця маси – гривна – була водночас грошовою одиницею. Гривна – це злиток срібла, маса якого наближено дорівнювала 1 фунту. У другій половині ХІІІ ст. гривну почали рубати навпіл і називати рублем, який із Х\/ став основною грошовою одиницею. Нині в Україні гривна – грошова одиниця. У творах Архімеда та “Началах” Евкліда були виведені формули для знаходження об'ємів многогранників і деяких тіл обертання (циліндра, кулі, конуса та їх частин). Розробив теорію площ і об'ємів К.М.Е.Жордан (1838 - 1922) – французький математик, один із засновників сучасної математики. У минулому одиницями вимірювання об'ємів біли міри посудини, що використовувалися для зберігання сипучих і рідких речовин. Евклід Приблизно 330 – 277 до н.е.

ПОНЯТТЯ ОБ’ЄМУ Для простих тіл об’єм – це додатна величина, числове значення якої має такі властивості: 1. Рівні тіла мають рівні об’єми. 2. Якщо тіло розбито на частини, які є простими тілами, то об’єм цього тіла дорівнює сумі об’ємів його частин. 3. Об’єм куба, ребро якого дорівнює одиниці довжини, дорівнює одиниці. Пригадай, які одиниці вимірювання об’ємів використовують в математиці?

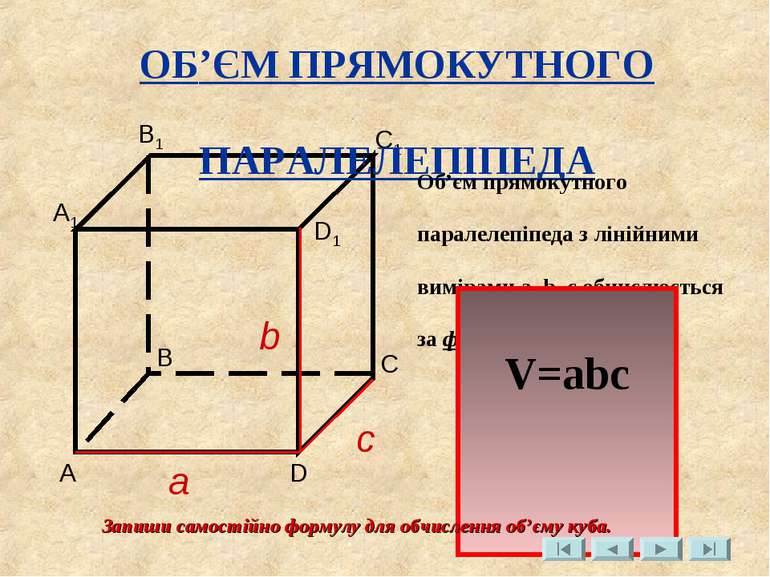
a b c A B С D A1 B1 D1 С1 ОБ’ЄМ ПРЯМОКУТНОГО ПАРАЛЕЛЕПІПЕДА Об’єм прямокутного паралелепіпеда з лінійними вимірами a, b, c обчислюється за формулою: V=abc Запиши самостійно формулу для обчислення об’єму куба.

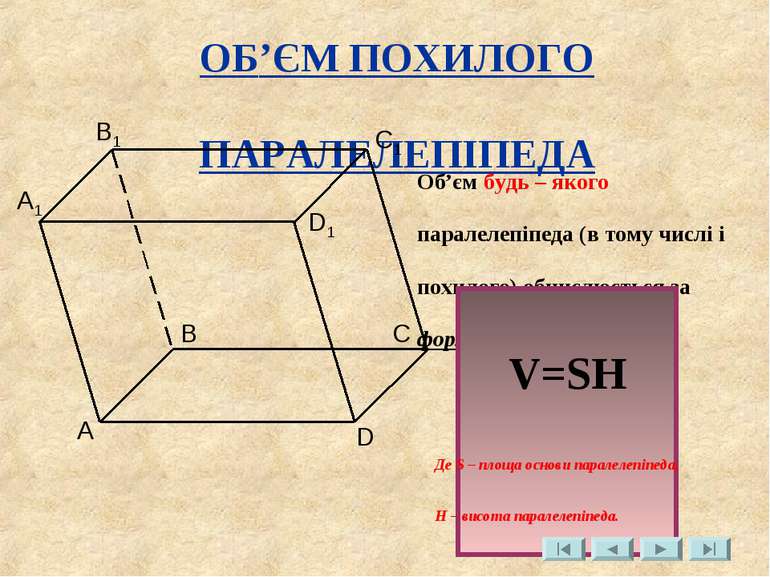
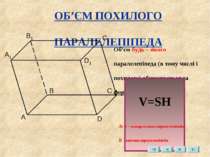
ОБ’ЄМ ПОХИЛОГО ПАРАЛЕЛЕПІПЕДА Об’єм будь – якого паралелепіпеда (в тому числі і похилого) обчислюється за формулою: V=SH Де S – площа основи паралелепіпеда, H – висота паралелепіпеда.

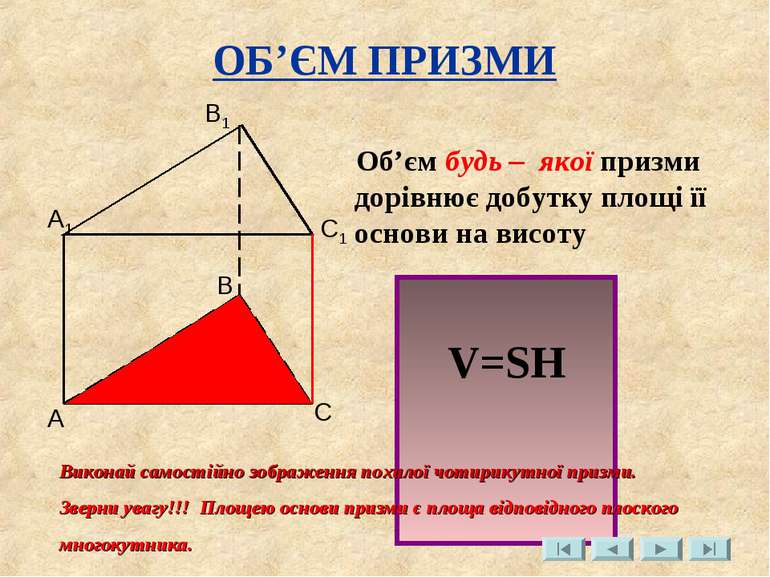
ОБ’ЄМ ПРИЗМИ Об’єм будь – якої призми дорівнює добутку площі її основи на висоту V=SH A B С A1 B1 С1 Виконай самостійно зображення похилої чотирикутної призми. Зверни увагу!!! Площею основи призми є площа відповідного плоского многокутника.

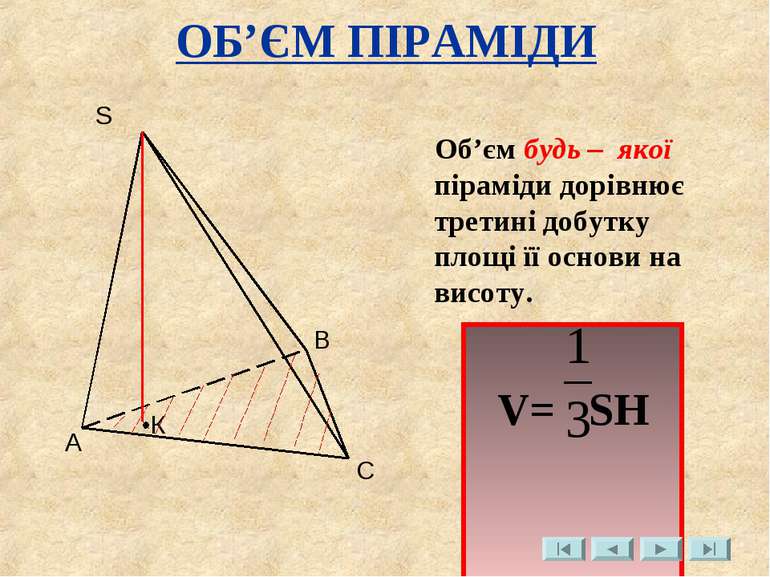
ОБ’ЄМ ПІРАМІДИ Об’єм будь – якої піраміди дорівнює третині добутку площі її основи на висоту. A B S С К

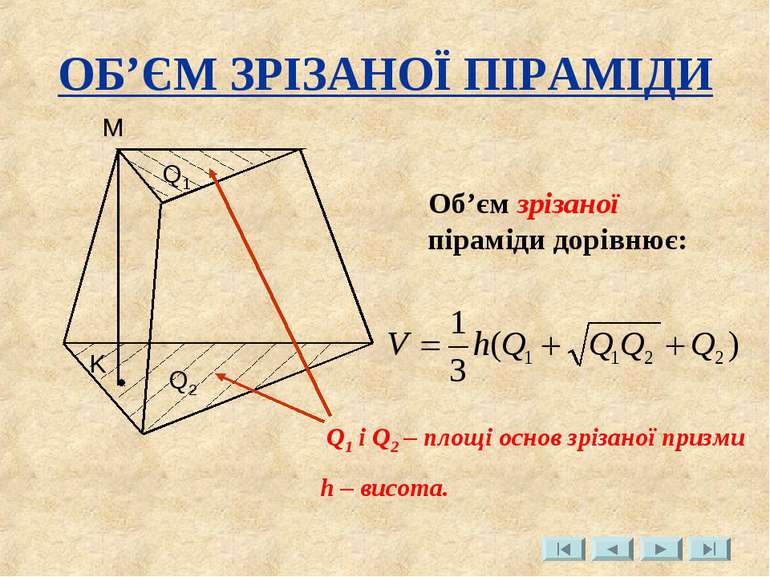
ОБ’ЄМ ЗРІЗАНОЇ ПІРАМІДИ Q1 Q2 Об’єм зрізаної піраміди дорівнює: M K Q1 і Q2 – площі основ зрізаної призми h – висота.

ЄГИПЕТСЬКІ ПІРАМІДИ Великі піраміди в Гізі Ступінчата піраміда Джосера Червона піраміда Снофру Велика піраміда Хеопса

Довідкова інформація Єги петські пірамі ди — найбільший архітектурний пам'ятник з семи чудес світу. Піраміди — це величезні камяні споруди пірамідальної, ступінчатої чи баштоподібної форми, збудовані як гробниці для фараонів Давнього Єгипту. При згадці єгипетських пірамід, як правило, мають на увазі розташовані в Гізі, неподалік від Каїру Великі Піраміди. Проте, вони не були єдиними пірамідами Єгипту. Перша піраміда — ступінчата піраміда Джосера, побудована приблизно в 2670 року до нашої ери, нагадує кілька поставлених один на одного щораз менших мастаб. Швидше за все, саме таким був задум архітектора цієї піраміди, Імхотепа. Імхотеп розробив спосіб кладки з тесаного каменю. Згодом, єгиптяни глибоко шанували зодчого першої піраміди, і навіть обожествили його. Він вважався сином бога Птаха, покровителя мистецтв і ремесел. Сама піраміда Джосера розташована в Саккарі, неподалік від древнього Мемфіса. Її висота становить 62 метри. Фараон Снофру, батько Хеопса, побудував першу піраміду з рівними стінами - Червону піраміду. Найбільшою є піраміда Хеопса. Спочатку її висота становила 147 метрів, проте, через те, що нині відсутнє облицювання піраміди, її висота натепер зменшилася на 7,5 метрів. Довжина сторони піраміди — 230 метрів. Піраміда була побудована XXVII столітті до н. е. Припускають, що будівництво тривало 23 роки. Піраміда складена з 2,3 мільйонів кам'яних блоків, які були підігнані один до одного з неперевершеною точністю. При цьому не використовувався цемент чи інші сполучні речовини. Кожен блок важить 2 тонни. Піраміда є практично монолітним спорудженням — за винятком поховальної камери і провідних до неї коридорів, в піраміді практично немає внутрішнього простору.

Розв'яжіть задачі: Початковий рівень Обчисліть об’м похилого прямокутного паралелепіпеда, якщо сторони його основи 4 см і 6 см, а висота рівна 10 см. Об’єм призми 300 см3, площа її основи дорівнює 30 см2. Обчисліть висоту призми. В основі піраміди лежить паралелограм, одна сторона якого рівна 8 см, а висота, проведена до цієї сторони, дорівнює 5 см. Обчисліть об’єм піраміди, якщо її висота дорівнює 6 см. Середній рівень Основа прямокутного паралелепіпеда – квадрат. Знайти об'єм цього паралелепіпеда, якщо його висота 4 см, а діагональ бічної грані утворює з площиною основи кут 45°. 2. В основі призми лежить ромб з діагоналями 2 см і 3 см, висота призми рівна 4 см. Обчисліть об'єм даної призми. 3. Основою піраміди є трапеція з основами 8 см і 12 см і висотою 4 см. Висота піраміди дорівнює 6 см. Знайти об'єм піраміди.

Розв'яжіть задачі: Достатній рівень Діагональ прямокутного паралелепіпеда дорівнює d і нахилена до площини основи під кутом . Кут між стороною і діагоналлю основи дорівнює Визначити об'єм паралелепіпеда. 2. В основі прямої призми лежить прямокутний трикутник із кутом і протилежним катетом b. Діагональ грані, що містить гіпотенузу цього трикутника, утворює з площиною основи кут . Визначити об'єм призми. 3. В основі піраміди лежить рівнобедрений трикутник з кутом 30° при основі і радіусом вписаного кола 5 см. Визначити об'єм піраміди, якщо всі її бічні грані утворюють з площиною основи кут 45°. Високий рівень Основою похилого паралелепіпеда є прямокутник зі сторонами 4 см і 8 см. Одне з бічних ребер паралелепіпеда дорівнює 3 см і утворює з сторонами основи кути по 45°. Визначити об'єм паралелепіпеда. 2. Визначити об'єм правильної трикутної зрізаної піраміди, якщо радіуси вписаних в основу кіл відповідно дорівнюють 3 і 5 см, а бічне ребро 4 см нахилене до площини основи під кутом 60°. Розв'яжіть задачі: