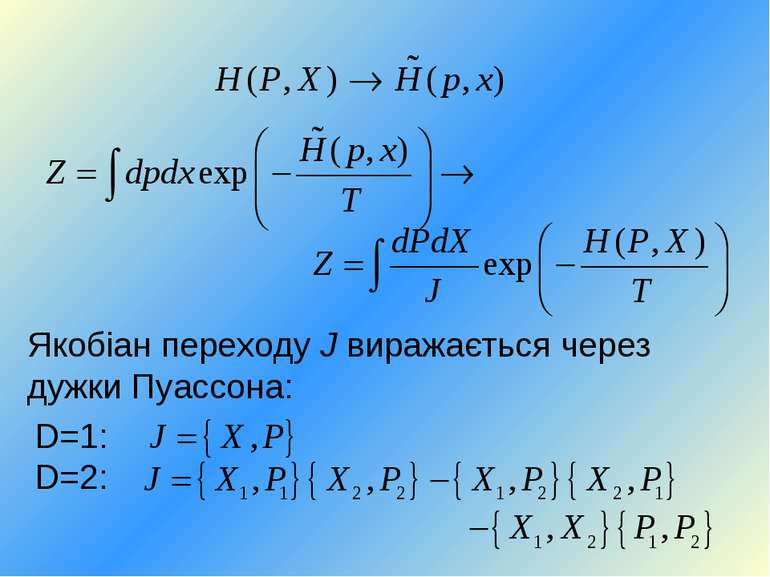Презентація на тему:
Статистична фізика у деформованих просторах з найменшою довжиною

Статистична фізика у деформованих просторах з мінімальною довжиною Тарас Фітьо кафедра теоретичної фізики, Львівський національний університет

Зміст Деформовані алгебри Постановка задачі Наслідки мінімальної довжини Приклад Висновки

Невизначеність координати: Деформований комутатор Кемпфа: Маджіоре: Деформовані алгебри Maggiore M., A generalized uncertainty principle in quantum gravity, Phys. Lett. B. 304, 65 (1993). Kempf A. Uncertainty relation in quantum mechanics with quantum group symmetry, J. Math. Phys. 35 4483 (1994).

Постановка задачі Статистичні властивості задаються Наближено – канонічно спряжені координати.

Chang L. N. et al, Effect of the minimal length uncertainty relation on the density of states and the cosmological constant problem, Phys. Rev. D. 65, 125028 (2002). Загальний вигляд деформованої алгебри Завжди можна вибрати канонічно спряжені змінні, такі що задовольняють деформованим дужкам Пуассона.

Якобіан переходу J виражається через дужки Пуассона: D=1: D=2:

Наслідки мінімальної довжини Мінімальна довжина приводить до або швидше для великих значень При великих кінетична енергія як В гамільтоніані Шредінгера: При високих температурах Вклад в теплоємність кінетичної енергії рівний нулю. Мінімальна довжина “з'їдає” поступальні ступені вільності.

Приклад: гармонічні осцилятори Статистична сума: Деформовані комутатори Кемпфа: Гамільтоніан 1 частинки:

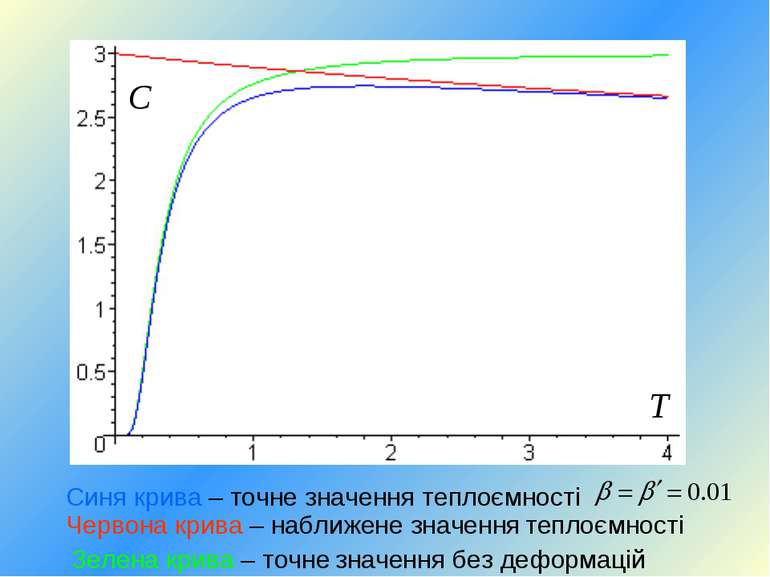
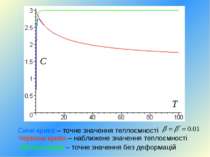
Синя крива – точне значення теплоємності Зелена крива – точне значення без деформацій Червона крива – наближене значення теплоємності

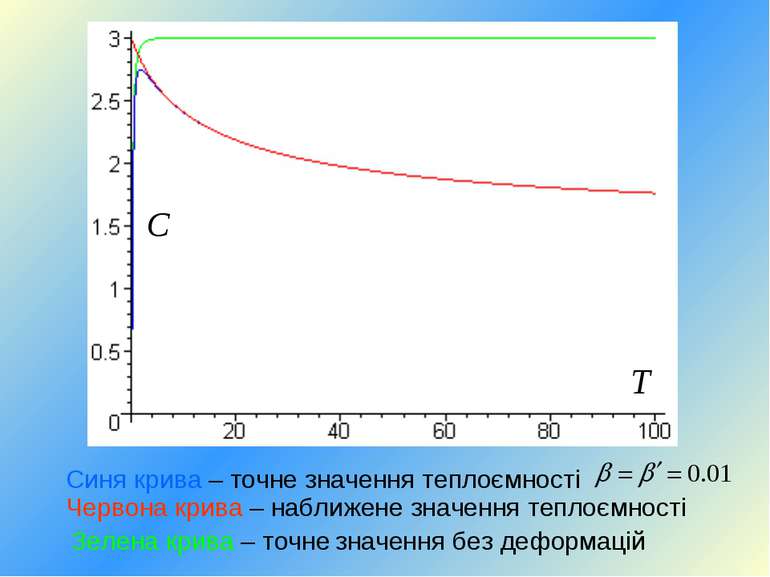
Синя крива – точне значення теплоємності Зелена крива – точне значення без деформацій Червона крива – наближене значення теплоємності

Висновки Отримано зручне наближення для статистичної суми, яке легко аналізувати. Показано, що мінімальна довжина зменшує теплоємність системи у границі високих температур.

Дякую за увагу. T. Fityo, Statistical physics in deformed space with minimal length, arXiv: 0712.0891 (2008).