Презентація на тему:
Вплив людини на стан Біосфери

Перетворення раціональних виразів (теоретичний мінімум) Вчитель: Бабій А.І.

1. Теоретичні поняття: вираз, раціональний вираз(цілий та дробовий). Формули скороченого множення. Числові вирази складаються з чисел за допомогою знаків дій і дужок. Якщо числовий вираз містить ще й літери (або тільки літери), які позначають числа або змінні, то воно називається алгебраїчним виразом. Алгебраїчне вираз, в якому є додавання, множення, ділення і піднесення до ступеня (натуральне число), називається раціональним алгебраїчним виразом.  Якщо раціональний алгебраїчний вираз не містить операції ділення на вираз зі змінними, то він називається цілим.   Якщо при складанні раціонального алгебраїчного виразу використовується операція ділення на вираз зі змінними, то такий вираз називається дробовим.

Формули скороченого множення

Правила розв'язування вправ, що містять перетворення раціональних виразів. Перетворення будь-якого раціонального виразу можна звести до дода вання, віднімання, множення та ділення раціональних дробів. Суму, різницю, добуток і частку раціональних дробів завжди можна подати у вигляді раціонального дробу. Будь-який раціональний вираз можна подати у вигляді раціонального дробу. Для цього: а) встановлюємо (визначаємо), які дії з раціональними дробами слід виконати, виходячи з умови завдання; б) виконуємо ці дії або у порядку спадання дії, або користуючись законами (властивостями) арифметичних дій (перестановка + і; сполучна + і; розпо дільна) та властивостями раціональних дробів (основною властивістю дробу)

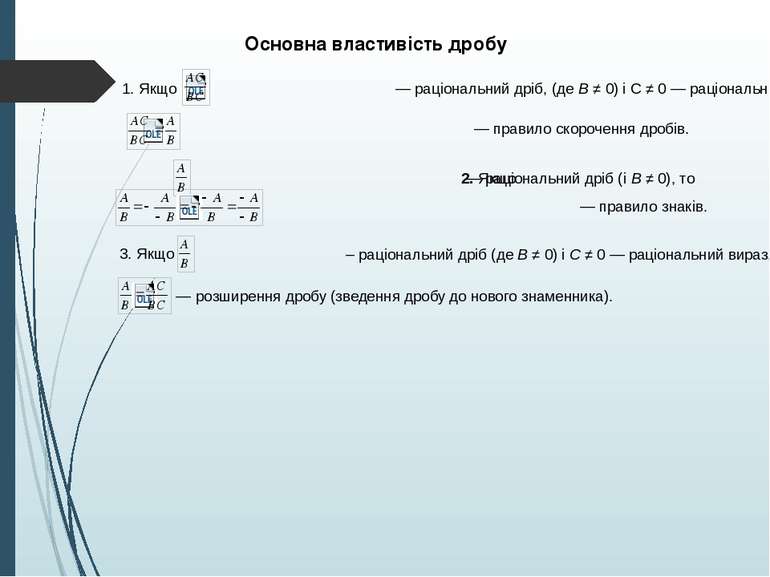
Основна властивість дробу 1. Якщо — раціональний дріб, (де В ≠ 0) і С ≠ 0 — раціональний вираз. — правило скорочення дробів. 2. Якщо — раціональний дріб (і В ≠ 0), то — правило знаків. 3. Якщо – раціональний дріб (де В ≠ 0) і С ≠ 0 — раціональний вираз, то — розширення дробу (зведення дробу до нового знаменника).

Додавання і віднімання дробів з рівними знаменниками Для будь-яких А, В, С, де С≠0 правильнірівності: Длябудь-яких А, В, С, де С≠ 0правильні рівності:

Для будь-яких А, В, С і D, де В ≠ 0 і D ≠ 0 правильні рівності: Причому BD — найменший спільний знаменник дробів і . Додавання і віднімання дробів з різними знаменниками

Множення, ділення, піднесення дробів до степеню 1. Для будь-яких А, В, С іDде В ≠ 0,D≠ 0, справджується рівність:   2. Для будь-яких А і В, В≠ 0,справджується рівність:   3. Для будь-яких А, В, С іDдеB≠ 0,C≠ 0,D≠ 0,справджується рівність:

Дякую за увагу!