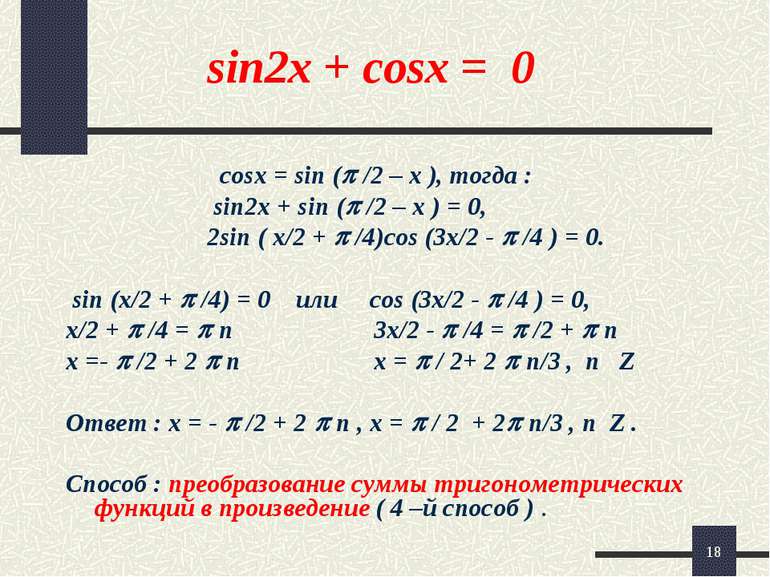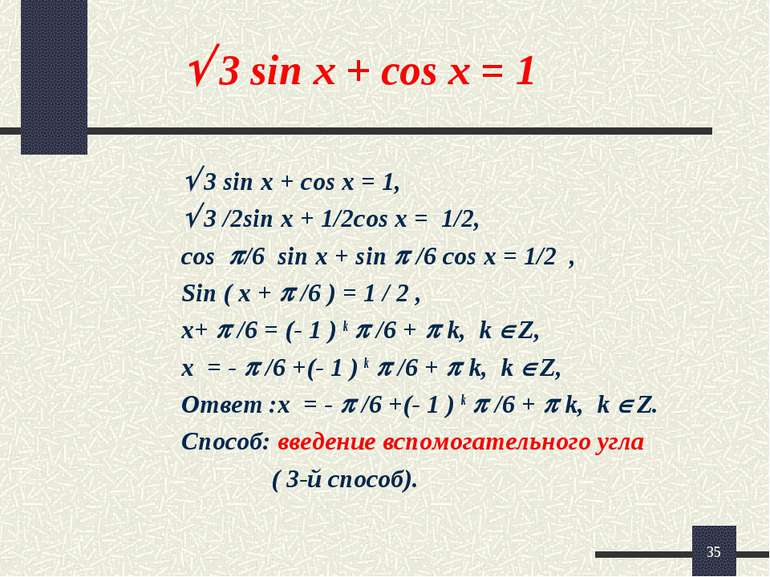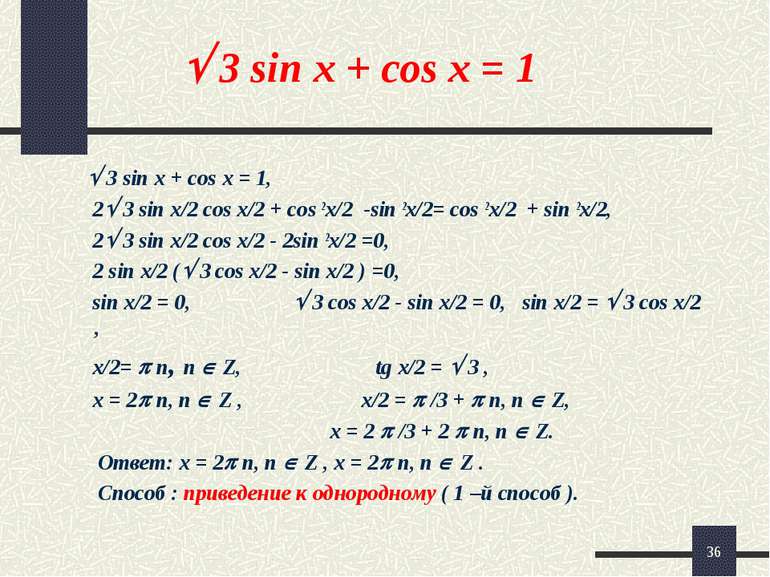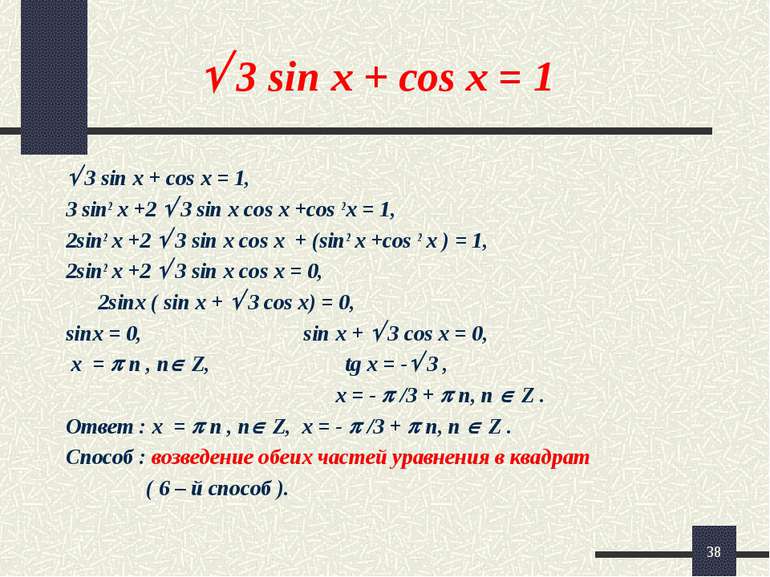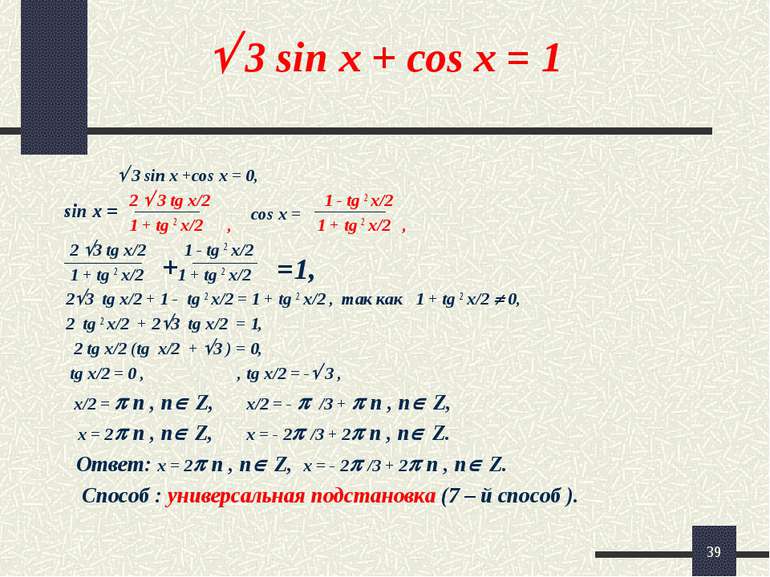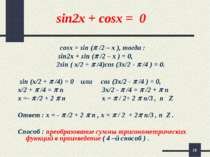Презентація на тему:
Вісім способів розв'язання одного тригонометричного рівняння

Алгебра и начала анализа 10 класс Восемь способов решения одного тригонометрического уравнения Учитель ОШ № 47 Писарева Елена Алексеевна

* Человеку, изучающему алгебру часто полезнее решить одну и ту же задачу тремя различными способами, чем решать три – четыре различные задачи. Решая одну задачу различными способами , можно путем сравнивания выяснить, какой из них короче и эффективнее. Так вырабатывается опыт. У. У. Сойер /английский математик и педагог XX века/

* Восемь способов решения одного тригонометрического уравнения. 1.Приведение уравнения к однородному. 2.Разложение левой части уравнения на множители. 3.Введение вспомогательного угла. 4.Преобразование разности (или суммы) тригонометрических функций в произведение. 5.Приведение к квадратному уравнению. 6.Возведение обеих частей уравнения в квадрат. 7.Универсальная подстановка. 8.Графическое решение.

* Задача. Решите уравнение различными способами: sin x – cos x = 1. ?

* Способ первый. Приведение уравнения к однородному. sin x – cos x = 1 Это однородное уравнение первой степени. Делим обе части этого уравнения на т.к., если что противоречит тождеству Получим: sin x = 2 sin x/2 cos x/2, cos x = cos 2 x/2 +sin 2 x/2, 1 = sin 2 x/2 + cos2 x/2. , .

* Способ второй. Разложение левой части уравнения на множители: sin x – cos x = 1 Далее так, как в первом способе.

* Способ третий. Введение вспомогательного угла. sin x – cos x =1 В левой части вынесем - корень квадратный из суммы квадратов коэффициентов при sin х и cos х. = sin /4 = cos /4 sin cos - cos sin = sin ( - )

* Внимание! Эквивалентны ли результаты , полученные в рассмотренных способах решений данного уравнения sin x – cos x = 1? Покажем однозначность ответов. 1 –й способ x = /2 + 2 n, n Z x: /2; 5 /2 ; 9 /2; -3 /2; -7 /2;… x = + 2 n, b Z x = ; 3 ; 5 ; - ; -3 ;… 2-й способ x = /4 + ( -1) /4 + k, k Z x: /2; ; 5 /2 ; 3 ; 9 /2; - ; - 3 /2; -3 ; -7 /2…

* Способ четвертый. Преобразование разности (или суммы) тригонометрических функций в произведение. sin x – cos x = 1 Запишем уравнение в виде: Применим формулу разности двух синусов. Далее так, как в третьем способе. 1 cos x = sin ( / 2 – x )

* Способ пятый. Приведение к квадратному уравнению относительно одной функции. sin x - cos x = 1 Возведем в квадрат: или

* Внимание! При решении уравнения обе части уравнения возводились в квадрат, что могло привести к появлению посторонних решений, поэтому необходима проверка. Сделаем проверку. Полученные решения эквивалентны объединению трёх решений Первое и второе решение совпадают с ранее полученными, поэтому не являются посторонними. Проверять не будем. Проверим: Левая часть: а правая часть уравнения равна 1, следовательно это решение является посторонним.

* Способ шестой.Возведение обеих частей уравнения в квадрат. sin x – cos x = 1 sin2x - 2sin x cos x + cos2 x = 1, sin2 x + cos2x = 1 1 – 2sin x cos x = 1, 2sin x cos x = 0, Ответ: x =п+2 n, n Z, x= /2 + 2 n, n Z. или cos x =0 x= /2 + n, n Z sin x = 0 x = n, n Z

* Способ седьмой. Универсальная подстановка (выражение sin x и cos x через tg x/2). sin x – cos x =1 Выражение всех функций через tg х (универсальная подстановка) по формулам: Sin x –cosx = 1 Умножим обе части уравнения на

* Внимание! Могли потерять корни.Необходима проверка! Область допустимых значений первоначального уравнения - всё множество R . При переходе к tg x/2 из рассмотрения выпали значения x, при которых tg x/2 не имеет смысла, т.е.x = +2 n, где n Z . Следует проверить , не является ли x = +2 n, где n Z решением данного уравнения. Левая часть sin(π + 2πk) – cos(π + 2πk) = sin π – cos π = 0 – (-1) = 1 и правая часть равна единице. Значит, x = + n ,где n Z является решением данного уравнения. Ответ: : x= п+2 n, n Z, x= /2 +2 n, n Z.

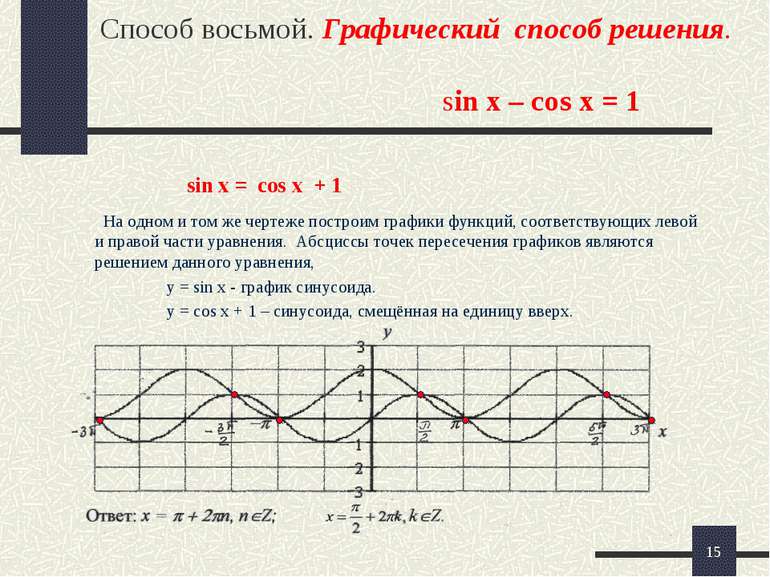
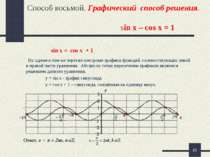
* Способ восьмой. Графический способ решения. sin x – cos x = 1 На одном и том же чертеже построим графики функций, соответствующих левой и правой части уравнения. Абсциссы точек пересечения графиков являются решением данного уравнения, у = sin х - график синусоида. у = соs х + 1 – синусоида, смещённая на единицу вверх. sin x = cos x + 1

* Проверь себя ! Решите самостоятельно, применяя разные способы решения одного и того же тригонометрического уравнения: 1. sin2x + cosx = 0 ; 2. 3 sin x – cos x = 0 3. sin6x + sin3x = 0; 4. sin2x +cos2x = 1; 5. 3sin x + cos x = 1.

* sin2x + cosx = 0 sin2x =2sinxcosx, тогда 2sinxcosx + cosx = 0, cosx( 2sinx + 1 ) = 0, cosx = 0 или 2sinx + 1 = 0, х = /2 + n; n Z; sinx = -1/2 x = ( -1)k+1 /6 + k, k Z. Ответ: x = /2 + n, ; x = (-1)k+1 /6 + k , где n Z , k Z . Способ: разложение левой части уравнения на множители ( 2-й способ ).

* sin2x + cosx = 0 cosx = sin ( /2 – x ), тогда : sin2x + sin ( /2 – x ) = 0, 2sin ( x/2 + /4)cos (3x/2 - /4 ) = 0. sin (x/2 + /4) = 0 или cos (3x/2 - /4 ) = 0, x/2 + /4 = n 3x/2 - /4 = /2 + n x =- /2 + 2 n x = / 2+ 2 n/3 , n Z Ответ : x = - /2 + 2 n , x = / 2 + 2 n/3 , n Z . Способ : преобразование суммы тригонометрических функций в произведение ( 4 –й способ ) .

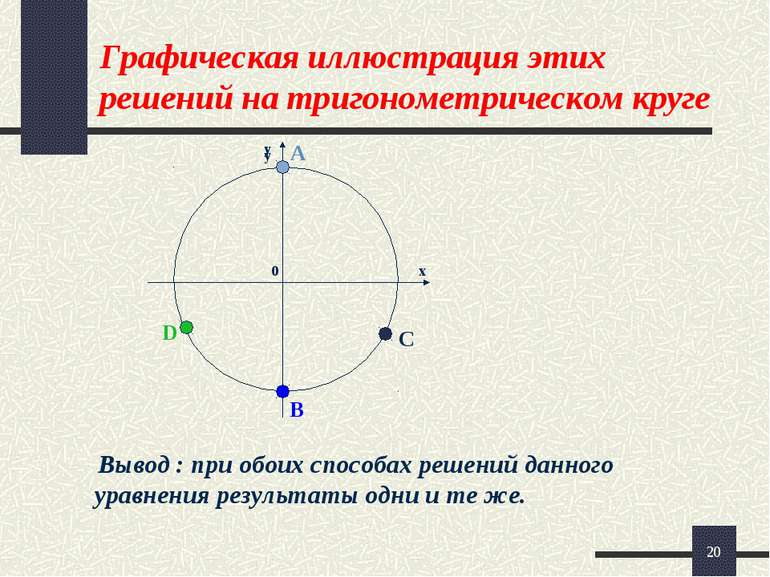
* Сравним результаты двух способов решения уравнения sin2x + cosx = 0 2 –й способ: x = /2 + n; n Z, n =0, x = /2 ( т. A ), n = 1, x = 3 /2 (т. В ), n =-1, x = - /2 ( т. В ), n = 2, x = /2 +2 (т.А) 2) x=(-1)k+1 /6 + k;k Z, k=0, x = - /6 ( т.C ), k =1, x = /6 + (т.D ), k =-1, x = /6 - (т .D), k =2,x = - /6+2 (т.C) 4-способ: 1) x = - /2 + n, n Z , n =0, x= - /2, (т .В ), n =1, x =- /2 + 2 , (т .В ), n=-1, x= - /2 –2 , (т. В ), n=2, x = - / 2+ 4 ,(т .В ). 2) x = / 2 + 2 n/3 , n Z . n =0, x= /2 ( т.А ), n=1, x = 7 /6 ( т. D ), n= -1, x = - /6 (т. А), n = 2, x = 11 / 6 (т.С ),…

* Графическая иллюстрация этих решений на тригонометрическом круге Вывод : при обоих способах решений данного уравнения результаты одни и те же. 0 х у у А В С D

* 3 sin x – cos x = 0 cos x 0 в силу основного тригонометрического тождества sin2x + cos2x = 1. Разделим обе части уравнения на cos x. 3 tg x = 1, tg x = 1/ 3 , x = /6 + n , n Z. Ответ: x = /6 + n, n Z. Cпособ :решение однородного уравнения ( 1-й способ ).

* 3 sin x – cos x = 0 3sin x – cos x = 0, разделим обе части уравнения на 2. 3/2sin x – ½cos x = 0, sin x cos /6 – cos x sin /6 = 0, sin (x - /6) = 0, x - /6 = n , n Z, x = /6 + n , n Z. Ответ : x = /6 + n, n Z. Способ: введение вспомогательного угла ( 3 –й способ ).

* 3 sin x – cos x = 0 3 sin x – cos x = 0, возведем обе части уравнения в квадрат. 3 sin2x – 2 3 sin x cos x + cos2x = 1, разделим обе части уравнения на cos2x 0. 3 tg2x – 2 3 tg x + 1 = 0 D = 0, tg x = 3/ 3; x = /6 + n, n Z. Ответ :x = /6 + n, n Z. Способ :возведение обеих частей уравнения в квадрат ( 6-й способ). уравнения в

* 3 sin x – cos x = 0 3 sin x – cos x = 0, 2 tg x/2 1 - tg 2 x/2 1 + tg 2 x/2 , 1 + tg 2 x/2 , 3 2 tg x/2 1 - tg 2 x/2 1 + tg 2 x/2 1 + tg 2 x/2 3 2 tg x/2 - 1 + tg 2 x/2 1 + tg 2 x/2 1 + tg 2 x/2 0, tg 2 x/2 + 2 3 tg x/2 - 1 = 0, tg x/2 = m, m 2 + 2 3 m – 1 =0, D = 0, m1 = - 3 - 2, m2 = - 3 + 2, 1) tg x = - 3 - 2, 2(- 3 - 2 ) - 2( 3 + 2 ) - 2( 3 + 2 ) - 1 1 +( - 3 - 2)2 8-4 3 4( 2+ 3 ) 2 , sin x = - 1/2, x = ( -1 ) k +1 /6 + k, k Z; 2) tg x = - 3 + 2, 2(- 3 + 2 ) - 2( 3 - 2 ) - 2( 3 - 2 ) 1 1 +( - 3 + 2)2 8-4 3 4( 2- 3 ) 2 , sin x = 1/2, x = ( -1 ) k /6 + k, k Z. Примечание:решения можно объединить: x = ( -1 ) k /6 + k, k Z. Ответ: x = ( -1 ) k /6 + k, k Z. Способ: универсальная подстановка ( 7 –й способ ). sin x = cos x= - = = 0, =0, sin x= sin x = = = = = = =

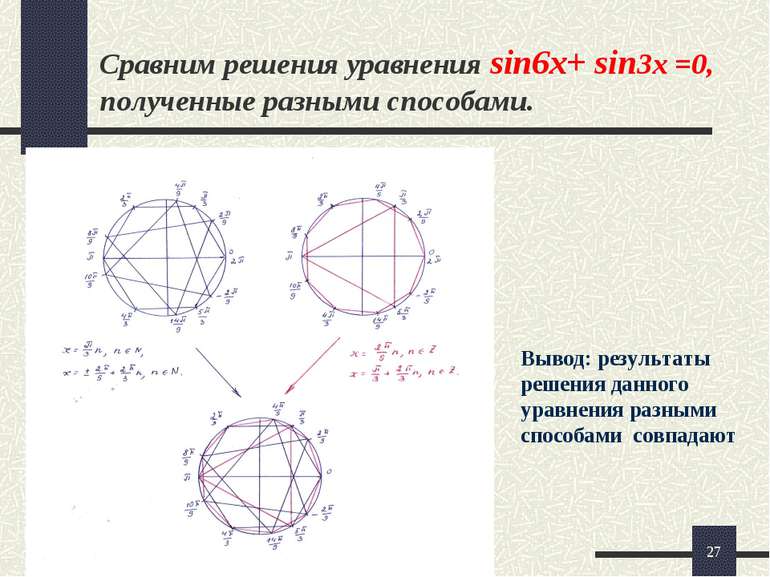
* sin 6x + sin 3x = 0 sin 6x + sin 3x = 0, 2 sin 3x cos 3x + sin 3x = 0, sin 3x ( 2 cos 3x + 1 ) = 0, sin 3x =0 , 2 cos 3x + 1 = 0, 3x = n, n Z, cos 3x = -½, x = n/3, n Z , x = 2 /9 + 2 n /3, n Z. Ответ: x = n/3, n Z; x = 2 /9 + 2 n /3, n Z. Способ:разложение левой части уравнения на множители ( 2 способ ).

* sin 6x + sin 3x = 0 sin 6x + sin 3x = 0, 2sin 9x/2 cos 3x/2 = 0 , sin 9x/2=0 , cos 3x /2 = 0, 9x/2 = n, n Z, 3x /2 = /2 + n, n Z, x = 2 n/9, n Z; x = /3 + 2 n/3, n Z . Ответ: x = 2 n/9, n Z; x = /3 + 2 n/3, n Z. Способ: преобразование тригонометрических функций в произведение ( 4-й способ ).

* Сравним решения уравнения sin6x+ sin3x =0, полученные разными способами. Вывод: результаты решения данного уравнения разными способами совпадают

* sin 2x + cos 2x = 1 sin 2x + cos 2x = 1 2 sin x cos x + cos 2 x – sin2 x = sin 2x + cos 2x, 2 sin x cos x – 2 sin 2 x = 0, 2 sin x ( cos x – sin x ) = 0, sin x = 0, cos x – sin x = 0, x = n, n Z, tg x = 1, x = /4 + n, n Z. Ответ: n, n Z, x = /4 + n, n Z. Способ: Приведение уравнения к однородному.( 1-й способ ).

* sin 2x + cos 2x = 1 sin 2x + cos 2x = 1, sin2x – (1 – cos 2x ) = 1, 2 sin x cos x – 2 cos 2x/2 = 0, Далее так, как первым способом ( кадр № 27 ). Способ: разложение левой части уравнения на множители ( 2 – й способ ).

* sin 2x + cos 2x = 1 sin 2x + cos 2x = 1, sin 2x + sin ( /2 – 2x ) = 1, 2sin /4 cos ( 2x - /4 ) = 1, sin /4 = 1/ 2 , 2 cos ( 2x - /4 )= 1 arksin (1 / 2 ) = /4 . cos ( 2x - /4 )= 1 / 2 , 2x - /4 = arkcos (1 / 2 ) + 2 n, n Z, 2x= /4 arkcos( 1 / 2 ) + 2 n, n Z, x= /8 /8 + n, n Z. Ответ: x= /8 /8 + n, n Z. Способ: преобразование суммы тригонометрических функций в произведение ( 4 –й способ ).

* sin 2x + cos 2x = 1 sin 2x + cos 2x = 1, разделим обе части уравнения на 2, 1/ 2 sin 2x + 1/ 2 cos 2x = 1/ 2 , cos /4 sin 2x + sin /4 cos 2x = 1/ 2, sin (2x + /4 ) = 1/ 2, 2x + /4 = (- 1)k /4 + k, k Z, 2x = - /4 + (- 1) k /4 + k, k Z, x = - /8 +(- 1)k /8 + k/2, k Z. Ответ: x = - /8 +(- 1)k /8 + k/2, k Z. Способ:Введение вспомогательного угла (3й – способ).

* sin 2x + cos 2x = 1 sin 2x + cos 2x = 1, Cos 2x = ( 1 - sin 2 2x ) sin 2x ( 1 - sin 2 2x ) = 1, ( 1 - sin 2 2x ) = 1 – sin 2x, возведем обе части уравнения в квадрат, тогда 1 - sin 2 2x = 1 – 2 sin 2x + sin 2 2x , 2 sin 2 2x - 2 sin 2x = 0, 2 sin 2x (sin 2x - 1 ) = 0, sin 2x = 0, sin 2x - 1 = 0, 2x = n, sin 2x = 1, x = n/2, n Z ; 2x = /2 + 2 n, n Z, x = /4 + n, n Z. Ответ: x = n/2, n Z ; x = /4 + n, n Z. Способ: приведение к квадратному уравнению относительно sin 2x ( 5 –й способ ).

* sin 2x + cos 2x = 1 sin 2x + cos 2x = 1, sin 2 2x + 2sin 2x cos 2x + cos 2x = 1, 2sin 2x cos 2x + 1 = 1, 2sin 2x cos 2x = 0, sin 2x = 0, cos 2x = 0 , 2x = n, n Z ; 2x = / 2 + 2 n , n Z, x = n/2, n Z ; x = / 4 + n , n Z. Ответ: / 2 + 2 n , n Z; x = / 4 + n , n Z. Способ : возведение обеих частей уравнения в квадрат ( 6 – й способ ).

* sin 2x + cos 2x = 1 sin2 x +cos 2x = 1, 2 tg x 1 - tg 2 x 1 + tg 2 x , 1 + tg 2 x , 2 tg x 1 - tg 2 x 1 + tg 2 x 1 + tg 2 x 2 tg x +1 - tg 2 x –1 - tg 2 x - 0, 1 + tg 2 x/2 0, 2tg 2 x - 2 tg x = 0, 2tg x ( tg x – 1 ) = 0, tg x =0, tg x – 1 = 0, sin 2x = 0, sin 2x = 1, x = n/2, n Z , 2x = /2 + 2 n, n Z, x = /4 + n, n Z. Ответ: x = n/2, n Z ; x = /4 + n, n Z. Способ: универсальная подстановка ( 7 –й способ ). sin 2x = cos2 x = + = 0

* 3 sin x + cos x = 1 3 sin x + cos x = 1, 3 /2sin x + 1/2cos x = 1/2, cos /6 sin x + sin /6 cos x = 1/2 , Sin ( x + /6 ) = 1 / 2 , x+ /6 = (- 1 ) k /6 + k, k Z, x = - /6 +(- 1 ) k /6 + k, k Z, Ответ :x = - /6 +(- 1 ) k /6 + k, k Z. Способ: введение вспомогательного угла ( 3-й способ).

* 3 sin x + cos x = 1 3 sin x + cos x = 1, 2 3 sin x/2 cos x/2 + cos 2x/2 -sin 2x/2= cos 2x/2 + sin 2x/2, 2 3 sin x/2 cos x/2 - 2sin 2x/2 =0, 2 sin x/2 ( 3 cos x/2 - sin x/2 ) =0, sin x/2 = 0, 3 cos x/2 - sin x/2 = 0, sin x/2 = 3 cos x/2 , x/2= n, n Z, tg x/2 = 3 , x = 2 n, n Z , x/2 = /3 + n, n Z, x = 2 /3 + 2 n, n Z. Ответ: x = 2 n, n Z , x = 2 n, n Z . Способ : приведение к однородному ( 1 –й способ ).

* 3 sin x + cos x = 1 3 sin x + cos x = 1, 2 3 sin x/2cos x/2 = 1 – cos x, 1 – cos x = 2 cos 2 x/2 2 3 sin x/2cos x/2 = 2 cos 2 x/2, 2 3 sin x/2cos x/2 - 2 cos 2 x/2 = 0, 2 cos x/2 ( 3 sin x/2 - cos x/2) = 0, Далее решать так как в первом способе. Способ: разложение левой части уравнения на множители ( 2 –й способ).

* 3 sin x + cos x = 1 3 sin x + cos x = 1, 3 sin2 x +2 3 sin x cos x +cos 2 x = 1, 2sin2 x +2 3 sin x cos x + (sin2 x +cos 2 x ) = 1, 2sin2 x +2 3 sin x cos x = 0, 2sinx ( sin x + 3 cos x) = 0, sinx = 0, sin x + 3 cos x = 0, x = n , n Z, tg x = - 3 , x = - /3 + n, n Z . Ответ : x = n , n Z, x = - /3 + n, n Z . Способ : возведение обеих частей уравнения в квадрат ( 6 – й способ ).

* 3 sin x + cos x = 1 3 sin x +cos x = 0, 2 3 tg x/2 1 - tg 2 x/2 1 + tg 2 x/2 , 1 + tg 2 x/2 , 2 3 tg x/2 1 - tg 2 x/2 1 + tg 2 x/2 1 + tg 2 x/2 2 3 tg x/2 + 1 - tg 2 x/2 = 1 + tg 2 x/2 , так как 1 + tg 2 x/2 0, 2 tg 2 x/2 + 2 3 tg x/2 = 1, 2 tg x/2 (tg x/2 + 3 ) = 0, tg x/2 = 0 , , tg x/2 = - 3 , x/2 = n , n Z, x/2 = - /3 + n , n Z, x = 2 n , n Z, x = - 2 /3 + 2 n , n Z. Ответ: x = 2 n , n Z, x = - 2 /3 + 2 n , n Z. Способ : универсальная подстановка (7 – й способ ). sin x = cos x = + =1,

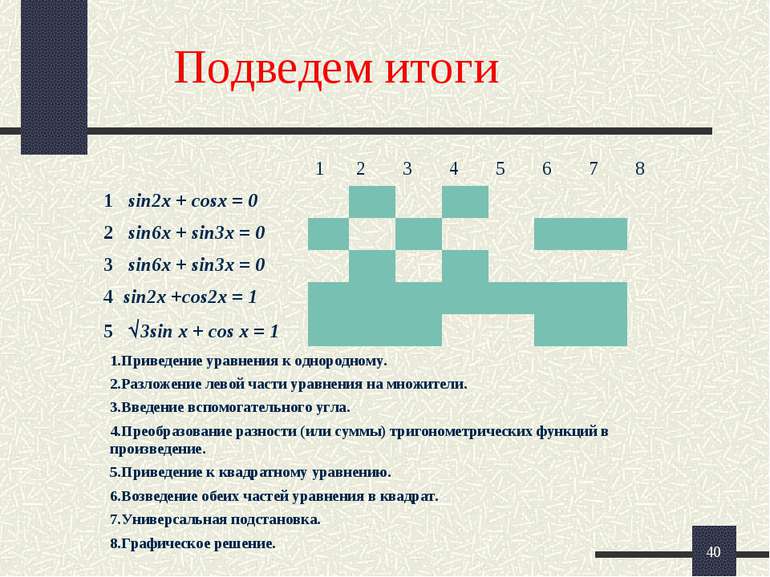
* Подведем итоги 1.Приведение уравнения к однородному. 2.Разложение левой части уравнения на множители. 3.Введение вспомогательного угла. 4.Преобразование разности (или суммы) тригонометрических функций в произведение. 5.Приведение к квадратному уравнению. 6.Возведение обеих частей уравнения в квадрат. 7.Универсальная подстановка. 8.Графическое решение. 1 2 3 4 5 6 7 8 1 sin2x + cosx = 0 2 sin6x + sin3x = 0 3 sin6x + sin3x = 0 4 sin2x +cos2x = 1 5 3sin x + cos x = 1

* Оцени себя сам Реши уравнения : Ответы: 6. 3 sin x + cos x = 2, 1. x = /4 + n, n Z; 7. 3 sin x – cos x = 2, 2. x = /3 + n, n Z; 8. sin x + cos x = 2, 3. x = /6 +(- 1)k /4 + k, Z; 9. cos 2x – cos 4x = 0, 4. x = /3 + 2 n, n Z; 10. sin x - 3 cos x = 0. 5.x = n /3, n Z; x = n, n Z. Ключ к ответам: Номер уравнения 6 7 8 9 10 Номер ответа 4 3 1 5 2

* Предлагаем уравнения для тренировки и самоконтроля Желаем успеха!