Презентація на тему:
Випадкова подія.Ймовірність випадкової події

Випадкова подія. Ймовірність випадкової події Алгебра, 9 клас

Місце теми в програмі

Орієнтовний розподіл годин Урок 1. Основні поняття теорії ймовірностей. Подія та її види. Урок 2. Ймовірність події. Урок 3. Розв'язування задач на обчислення ймовірності події.

Основні поняття теорії ймовірностей Стохастичний експеримент - експеримент, точний результат (наслідок) якого передбачити неможливо. Випробування - кожне конкретне (окреме) проведення стохастичного експерименту. Елементарна подія - кожний можливий наслідок стохастичного експерименту. Простір елементарних подій - множина всіх можливих наслідків стохастичного експерименту.

Основні поняття теорії ймовірностей Приклади. 1. Підкидання монети один раз і фіксація грані, якою монета впаде догори. Множина всіх можливих наслідків складається з двох наслідків: «монета падає догори гербом» і «монета падає догори цифрою». Це можна записати так : г, ц . 2. Підкидання грального кубика один раз і фіксація кількості очок на грані, що випала догори. 1, 2, 3, 4, 5, 6 . 3. Фіксація номера кульки, яка викочується з лототрону в таких іграх, як лото «Забава», «Укрлото», «Спортлото» тощо. Множина містить усі числа, які відповідають номерам кульок. Оскільки в лото «Забава» в лототроні 75 кульок, то 1, 2, 3, …, 75 .

Поняття випадкової події Випадковими подіями (або просто подіями) називають деякі з підмножин простору елементарних подій . Події позначають великими латинськими буквами А, В, С тощо. Оскільки кожна подія є деякою множиною, то її можна задати переліком її елементів – елементарних подій, або словесно – описанням характеристичної властивості її елементів. Кожну елементарну подію е, з яких складається подія А, називають елементарною подією, що сприяє події А. Усі інші елементарні події е вважаються такими, що не сприяють події А.

Поняття випадкової події Наприклад, в експерименті з підкиданням грального кубика, де = {1, 2, 3, 4, 5, 6}, події А 2, 4, 6 («випала парна кількість очок») сприяє три елементарних події: 2, 4 і 6, а 1, 3 і 5 не сприяють події А. Події В = «випало не більше, ніж 6 очок» сприяють всі шість елементарних подій: 1, 2, 3, 4, 5, 6. Події С = «випало більше, ніж 6 очок» не сприяє жодна елементарна подія з простору .

Поняття випадкової події Якщо в результаті випробування відбулася елементарна подія, що сприяє події А, то кажуть, що в результаті цього випробування подія А відбулася. Якщо в результаті випробування не відбулася жодна з елементарних подій, що сприяють події А, то кажуть, що в результаті цього випробування подія А не відбулася.

Вірогідна та неможлива події Подія В = «випало не більше, ніж 6 очок» в результаті кожного випробування обов’язково відбудеться. Таку подію називають вірогідною (або достовірною). Інакше, вірогідною є подія, яка відбувається в результаті кожного випробування, пов’язаного з даним стохастичним експериментом. Подія С = «випало більше, ніж 6 очок» ніколи не може відбутися в результаті проведення експерименту. Таку подію називають неможливою. Інакше, неможливою є подія, яка не може відбутися в результаті будь-якого випробування, пов’язаного з даним стохастичним експериментом.

Рівні події Якщо подія В відбувається завжди, коли відбувається подія А, то кажуть: подія В спричинюється подією А або подія А спричинює подію В. Це означає, що кожна елементарна подія е, що сприяє події А, сприяє також і події В. Якщо подія А спричинює подію В і подія В спричинює подію А, то події А і В називають рівними і записують А = В. Це означає, що кожна елементарна подія, що сприяє події А, сприяє також і події В, та навпаки, кожна елементарна подія, що сприяє події В, сприяє також і події А. Інакше, події А і В рівні тоді і тільки тоді, коли вони одночасно відбуваються або не відбуваються.

Виконаємо завдання Які з наведених експериментів будуть стохастичними, а які ні? Відповідь пояснити: охолодження води при нормальному тиску до 0оС і фіксація її стану; витягування однієї карти з повної колоди і фіксація зображення на ній; розкручування колеса “Поля чудес” і фіксація сектора, де зупиниться стрілка; викочування кульки з лототрону лото “Укрлото” і фіксація зображеного на ній номера; змочення зрізу картоплі розчином йоду і фіксація зміни кольору поверхні картоплі.

Виконаємо завдання Указати простір елементарних подій таких експериментів: дворазове підкидання монети і фіксація пари зображень, що випали; монета підкидається тричі і фіксується поява кількості гербів; підкидання один раз двох гральних кубиків і фіксація пари очок, що випали; виконання одного пострілу в мішень, на якій зображено концентричні кола, занумеровані числами від 1 до 10 (вважається, що промах неможливий); по мішені виконується два постріли і фіксується кількість влучень.

Виконаємо завдання Указати, скільки елементарних подій містить простір , що відповідає даному експерименту: з мішечка для гри в лото виймається одна бочечка з номером; навмання витягується одна кісточка доміно з повного набору; з нового відривного календаря на 2010 рік навмання виривається листок; картки з написаними на них буквами П, О, Д, І, Я перемішують і розкладають у ряд навмання та фіксують слово, що утворилося; з 10 карток, на яких записані цифри, навмання одна за одною виймають 3 картки і фіксують отримане число

Виконаємо завдання Указати загальну кількість елементарних подій даного експерименту і кількість елементарних подій, які сприяють даній події: навмання називають натуральне двоцифрове число; подія А – назване число ділиться на 5; навмання беруть і фіксують букву з розрізної абетки; подія С – взята буква називається одним голосним звуком; картки з цифрами 1, 2, 3, 4, 5 перемішують, розкладають у ряд і фіксують утворене число; подія А – утворилося парне число; подія В – утворилося число кратне 3; подія С – утворилося число кратне 9;

Виконаємо завдання Указати, скільки елементарних подій сприяє даній події: поява на верхній грані грального кубика не менше 5 очок; навмання взята буква із повного набору абетки – голосна; навмання витягнута карта з повної гральної колоди містить зображення людини; при дворазовому підкиданні монети хоча б один раз випадало зображення герба;

Виконаємо завдання Які з подій є а) вірогідними, б) неможливими: випадання на верхніх гранях двох гральних кубиків у сумі 13 очок; навмання вирваний листок із нового календаря містить число не більше за 31; влучення або промах при одному пострілі; виграш за одним білетом лотереї; витягування із коробки кольорової кулі, якщо в ній є 3 синіх і 5 червоних куль; витягування із коробки жовтої кулі, якщо в ній є 3 синіх і 5 червоних куль?

Виконаємо завдання Гральний кубик підкидають один раз і фіксують число очок, яке випало на верхній грані. Назвати елементарні події, що сприяють даним подіям: А – випало число очок менше за 3; В – випало парне число очок; С – випало непарне число очок; D – випало число очок кратне 3; E – випало число очок менше за 7; G – випало число очок кратне 7; K – випало число очок кратне 2; L – випало число очок не більше за 4. Які з названих подій є вірогідними? неможливими? Які з подій спричинюють одна іншу? Які події є рівними?

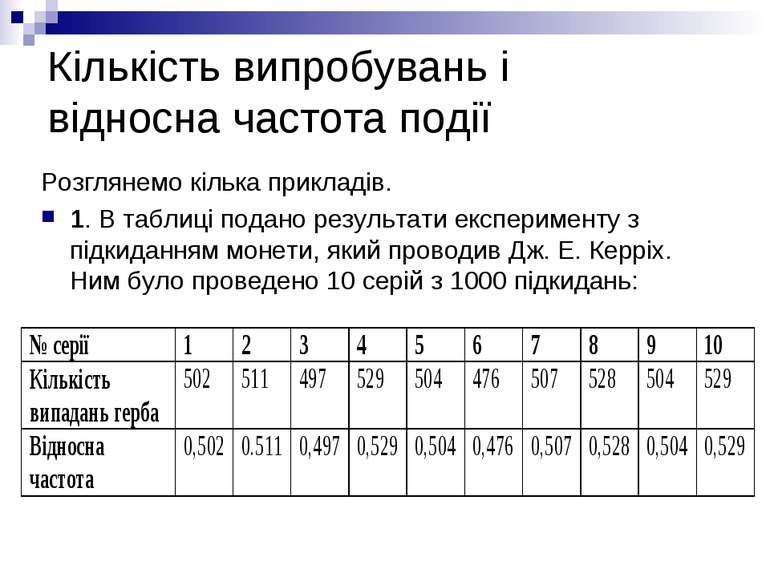
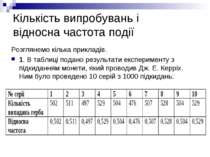
Кількість випробувань і відносна частота події Розглянемо кілька прикладів. 1. В таблиці подано результати експерименту з підкиданням монети, який проводив Дж. Е. Керріх. Ним було проведено 10 серій з 1000 підкидань:

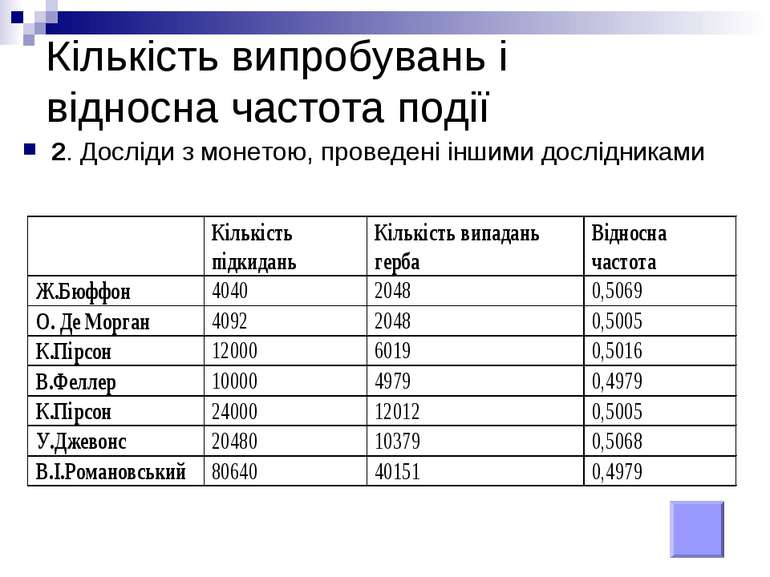
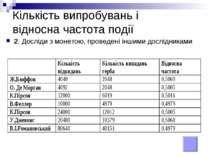
Кількість випробувань і відносна частота події 2. Досліди з монетою, проведені іншими дослідниками

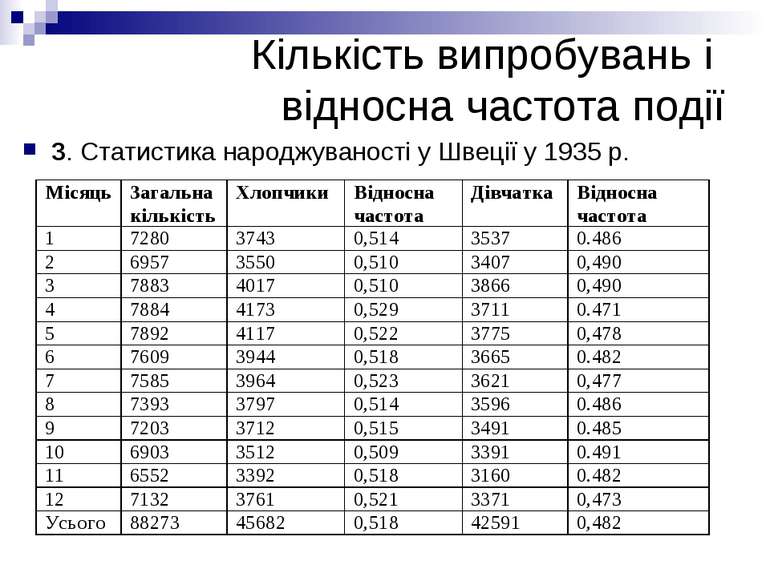
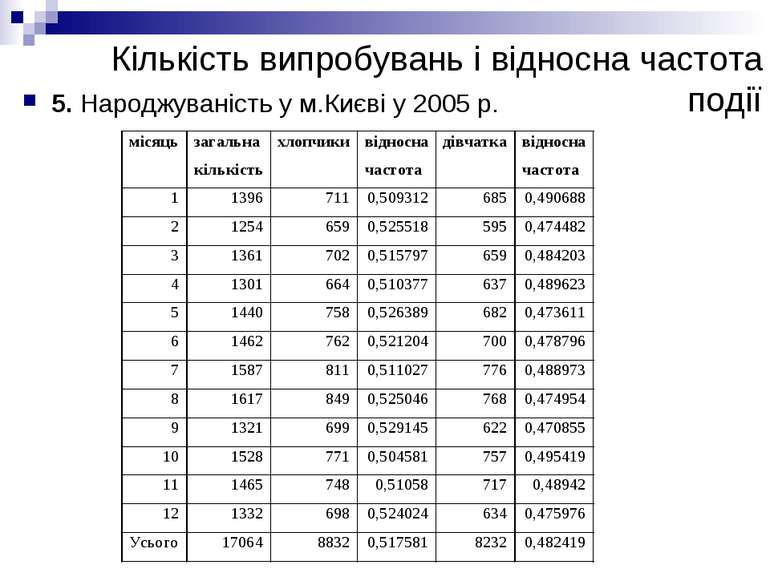
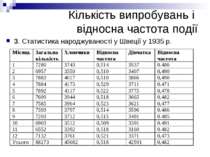
Кількість випробувань і відносна частота події 3. Статистика народжуваності у Швеції у 1935 р.

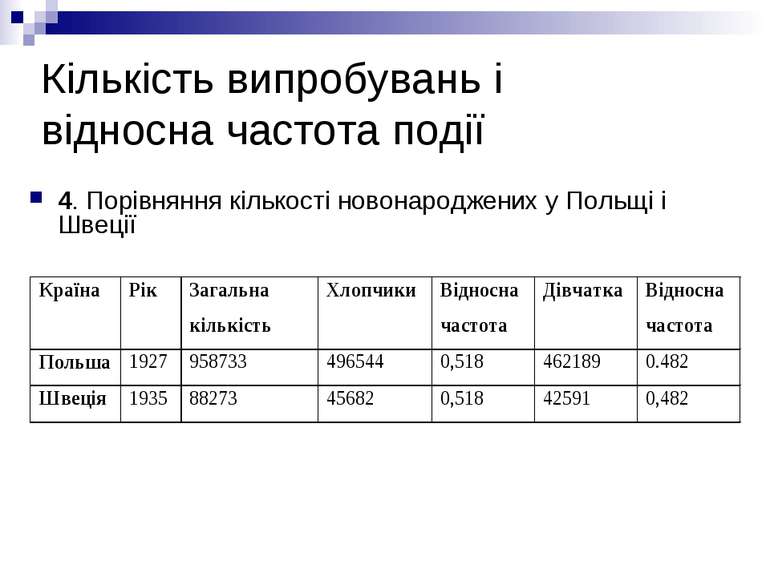
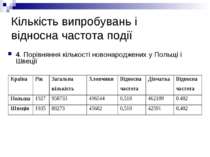
Кількість випробувань і відносна частота події 4. Порівняння кількості новонароджених у Польщі і Швеції

Кількість випробувань і відносна частота події 5. Народжуваність у м.Києві у 2005 р.

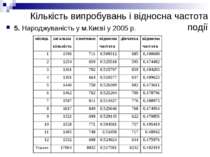
Поняття ймовірності події Приклади 1 і 2 показують, що хоча відносна частота випадання герба змінюється, вона мало відрізняються від числа 0,5. Приклади 3, 4 і 5 показують, що відносна частота народження хлопчиків мало відрізняється від числа 0,518. Можна навести ще чимало дослідів, у яких при достатньо великій кількості випробувань відносна частота кожної фіксованої події А майже не відрізняється від деякого числа Р(А), яке не залежить від кількості випробувань. Це число і називають ймовірністю події А.

Обчислення ймовірності події Якщо кожна з елементарних подій простору , пов’язаного з деяким експериментом, відбувається практично з однаковою частотою, то можна сказати, що такі елементарні події рівноможливі. де k – кількість елементарних подій, що сприяють події А, т – кількість усіх елементарних подій простору . Обчислення ймовірностей за таким правилом називають обчисленням ймовірності події за класичною схемою. За умови рівноможливості елементарних подій, що утворюють простір , ймовірність будь-якої події А обчислюється за формулою

Обчислення ймовірності події Наприклад: підкидаємо гральний кубик, = {1, 2, 3, 4, 5, 6}. Подія А 2, 4, 6 («випала парна кількість очок») Р(А) = 3/6 = 0,5 Подія D = 3, 6 («випала кількість очок кратна 3») Р(D) = 2/6 = 1/3 Подія В = «випало не більше, ніж 6 очок» Р(В) = 6/6 = 1 Подія С = «випало більше, ніж 6 очок» Р(В) = 0/6 = 0

Обчислення ймовірності події Якщо подія А – вірогідна, то Р(А) = 1 Якщо подія А – неможлива, то Р(А) = 0 Для ймовірності будь-якої події А має місце нерівність 0 Р(А) 1

Виконаємо завдання Чому дорівнює ймовірність кожної з вказаних подій: навмання називають натуральне двоцифрове число; подія А – назване число ділиться на 5; навмання беруть і фіксують букву з розрізної абетки; подія С – взята буква називається одним голосним звуком; картки з цифрами 1, 2, 3, 4, 5 перемішують, розкладають у ряд і фіксують утворене число; подія А – утворилося парне число; подія В – утворилося число кратне 3; подія С – утворилося число кратне 9;

Виконаємо завдання Чому дорівнює ймовірність кожної з вказаних подій: поява на верхній грані грального кубика не менше 5 очок; навмання взята буква із повного набору абетки – голосна; навмання витягнута карта з повної гральної колоди містить зображення людини; при дворазовому підкиданні монети хоча б один раз випадало зображення герба;

Виконаємо завдання У скарбничці є 200 монет, серед яких 25 монет 1992 року випуску. Яка ймовірність того, що навмання вибрана монета датована 1992 роком? На донорський пункт прийшли 12 осіб, серед яких 5 мають першу групу крові, 3 – другу і останні – третю. Яка ймовірність того, що перша людина, яка здала кров, має третю групу крові? Куб, усі грані якого пофарбовані, розпилено на 27 кубиків, які кинуто у торбу та перемішано. Визначити ймовірність того, що вийнятий навмання кубик має рівно дві пофарбовані грані.

Алгоритмічний припис обчислення ймовірності події за класичною схемою Опиши експеримент, про який йдеться в умові задачі та відповідний простір елементарних подій . Обґрунтуй рівноможливість елементарних подій і визнач, з яких елементарних подій складається подія А. Визнач кількість т елементарних подій простору Ω. Визнач кількість k елементарних подій, що сприяють події А. Обчисли ймовірність події А за формулою

Приклади задач Бевз Г.П., Бевз В.Г. Алгебра 9 Рівень А № 766. Пофарбований з усіх боків деревяний кубик розпиляли на 125 рівних кубиків і зсипали їх у торбину. Яка ймовірність того, що беручи з торбини кубик навмання, візьмете такий, у якого пофарбовано: а) три грані; б) тільки дві грані; в) тільки одна грань?

Приклади задач Бевз Г.П., Бевз В.Г. Алгебра 9 Рівень Б № 773. На 1000 білетів лотереї припадає 1 виграш 1000 грн, 10 виграшів по 200 грн, 50 – по 100 грн, 100 по 50 грн. Решта білетів невиграшні. Знайдіть імовірність виграшу на один білет, не меншого від 100 грн.

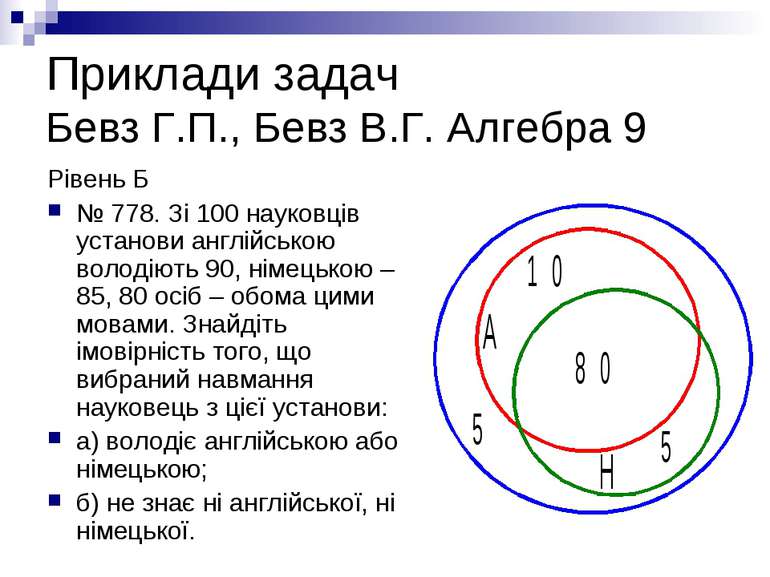
Приклади задач Бевз Г.П., Бевз В.Г. Алгебра 9 Рівень Б № 778. Зі 100 науковців установи англійською володіють 90, німецькою – 85, 80 осіб – обома цими мовами. Знайдіть імовірність того, що вибраний навмання науковець з цієї установи: а) володіє англійською або німецькою; б) не знає ні англійської, ні німецької.

Приклади задач Мерзляк А.Г., Полонський В.Б., Якір М.С. Алгебра 9 № 595о. Щоб скласти іспит з математики, потрібно вивчити 35 білетів. Учень вивчив бездоганно 30 білетів. Яка ймовірність того, що відповідаючи на один навмання витягнутий білет, він отримає оцінку 12 балів?

Приклади задач Мерзляк А.Г., Полонський В.Б., Якір М.С. Алгебра 9 № 607 . У коробці лежать 2 сині кульки і кілька червоних. Скільки червоних кульок у коробці, якщо ймовірність того, що взята навмання кулька: 1) виявиться синьою, дорівнює 2/5; 2) виявиться червоною, дорівнює 4/5?

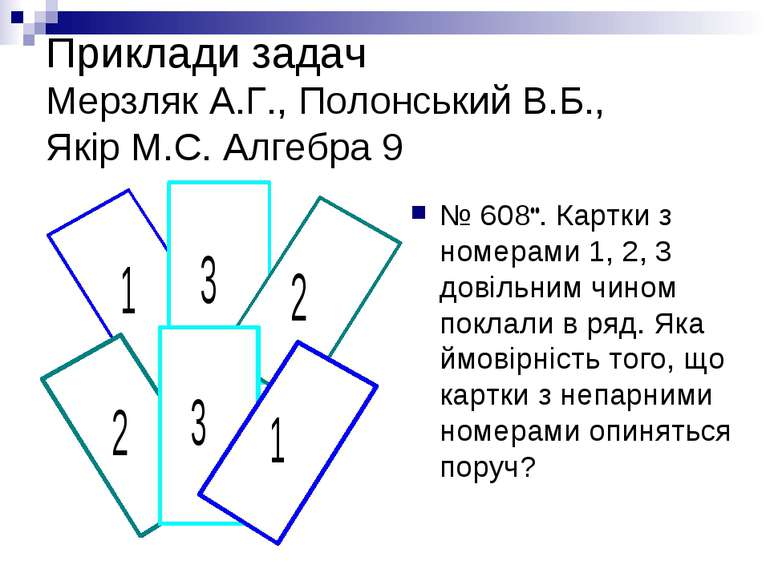
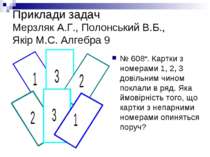
Приклади задач Мерзляк А.Г., Полонський В.Б., Якір М.С. Алгебра 9 № 608 . Картки з номерами 1, 2, 3 довільним чином поклали в ряд. Яка ймовірність того, що картки з непарними номерами опиняться поруч?

Приклади задач Мерзляк А.Г., Полонський В.Б., Якір М.С. Алгебра 9 № 614*. Яка ймовірність того, що при трьох кидках монети: 1) тричі випаде герб; 2) двічі випаде герб; 3) один раз випаде герб; 4) хоча б один раз випаде герб?

Приклади задач Кравчук В., Підручна М., Янченко Г. Алгебра 9 Рівень А № 578 У парку росте 360 дерев, з них 2/9 – хвойні. Знайдіть імовірність того, що навмання вказане дерево буде хвойним. Якою буде відповідь, якщо кількість усіх дерев дорівнюватиме 450? Зробіть висновок.

Приклади задач Кравчук В., Підручна М., Янченко Г. Алгебра 9 Рівень Б На трьох картках написано по одній букві: М, О, С. Картки перемішують і розкладають у ряд. Яка ймовірність того, що утвориться слово СОМ?

Приклади задач Кравчук В., Підручна М., Янченко Г. Алгебра 9 Рівень В № 592. Використовуючи цифри 1, 2, 3, 4, 5 не більше одного разу, навмання пишуть деяке трицифрове число. Знайдіть імовірність того, що це число виявиться парним.

Приклади задач Мальований Ю.І., Литвиненко Г. М., Возняк Г. М. Алгебра 9 № 392о. В урні міститься 10 однакових за розміром і різних за кольором кульок: 6 жовтих і 4 синіх. Кульки перемішали. Знайдіть ймовірність того, що навмання вийнята кулька виявиться синьою. № 393. В урні пронумеровано 100 жетонів (від 1 до 100). Яка ймовірність того, що номер навмання взятого з урни жетона не містить цифри 2?

Приклади задач Мальований Ю.І., Литвиненко Г. М., Возняк Г. М. Алгебра 9 № 397. Телефонна лінія, що сполучає населені пункти М і К, які знаходяться один від одного на відстані 4 км, обірвалася у невідомому місці. Яка ймовірність того, що обрив стався не далі, як за 750 м від пункту К?

Алгебра, 9 клас, поглиблене вивчення (12-річна школа)

Обчислення ймовірностей за допомогою правил комбінаторики 30.1о Навмання вибирають 4 букви зі слова “ЗАКОН”. Яка ймовірність того, що з вибраних букв можна скласти слово “КОЗА”? 30.7о У партії зі 100 лампочок є 7 бракованих. Яка ймовірність вибрати навмання з цієї партії 4 небраковані лампочки?

Обчислення ймовірностей за допомогою правил комбінаторики 30.11 У партії зі 100 деталей є 7 бракованих. Зцієї партії навмання вибирають 6 деталей. Яка ймовірність того, що серед вибраних 6 деталей 2 деталі виявляться бракованими? 30.13 Знайдіть ймовірність того, що дні народження 7 навмання вибраних людей припадають на різні дні тиждня.

Обчислення ймовірностей за допомогою правил комбінаторики 30.18 На екзамен з математики виносять 50 питань. Учень підготував тільки 40 питань. Білет складається з 6 питань, вибраних випадковим чином. Щоб скласти екзамен, достатньо відповісти на 4 питання білета. Яка ймовірність того, що учень складе екзамен?

Обчислення ймовірностей за допомогою правил комбінаторики 30.20 У ліфт 9-ти поверхового будинку на 1-му поверсі ввійшли 5 пасажирів. Кожний з них з однаковою ймовірністю може вийти на будь-якому поверсі, починаючи з 2-го. Знайдіть ймовірність події: Усі пасажири вийдуть на 9-му поверсі; Усі пасажири вийдуть на одному поверсі; Усі пасажири вийдуть на різних поверхах; Усі пасажири вийдуть до п'ятого поверху.