Презентація на тему:
https://svitppt.com.ua

Арифметична прогресія, її властивості. Формула n-го члена арифметичної прогресії. Перша умова, якої треба дотримуватися в математиці, – це бути точним, Друга – бути чітким, І наскільки можливо, простим. Сьогодні на уроці ми повинні…

Математичний кросворд Назва графіка квадратичної функції. Рівність, що містить одну або кілька змінних (невідомих). Алгебраїчний вираз, який містить в собі добуток двох або більше множників. Частина математики, яка вивчає просторові відношення і форми тіл. Результат дії віднімання. Старогрецький математик, якого прийнято називати «батьком геометрії». Результат додавання значень однорідних величин. Дійсні числа, які не є раціональними (наприклад число π). Хто відповідає на це запитання? 1   2   3   4   5   6   7   8   9  

Математичний кросворд Назва графіка квадратичної функції. Рівність, що містить одну або кілька змінних (невідомих). Алгебраїчний вираз, який містить в собі добуток двох або більше множників. Частина математики, яка вивчає просторові відношення і форми тіл. Результат дії віднімання. Старогрецький математик, якого прийнято називати «батьком геометрії». Результат додавання значень однорідних величин. Дійсні числа, які не є раціональними (наприклад число π). Хто відповідає на це запитання? 1   п а р а б о л а           2    р і  в  н  я  н  н  я            3   о  д  н  о  ч  л  е  н            4   г  е  о  м  е  т  р  і  я          5    р  і  з  н  и ц  я              6    е в к  л  і  д                7    с у  м  а                    8    і р  р  а  ц  і  о  н  а  л  ь  н  і  9    я                        

Активізація опорних знань  

Визначити способи задання послідовностей: а) ( bn ): 0,1; 7; 0,2; 8; 0,3; 9. (перелік членів послідовності) б) ( bn ): дільники числа 24 (опис знаходження членів послідовності) в) (табличний) г ) an = 5n; an = 2 n + 1. (формула) д ) an+1 = an ∙ 3, а1 = 4. (рекурентний) 3 4 5 9 16 25

Означення арифметичної прогресії Записати послідовність натуральних чисел, які при діленні на 2 дають в остачі 1. 3; 5; 7; 9; 11;… Така послідовність є прикладом арифметичної прогресії. Отже, арифметичною прогресією називають послідовність, кожний член якої, починаючи із другого, дорівнює попередньому члену, до якого додається одне й те ж число. Це число називається різницею арифметичної прогресії та позначають буквою d. Тоді арифметичну прогресію можна задати рекурентною формулою: аn+1 = an + d, звідки d = an+1 - an Приклади арифметичної прогресії: А) 1, 2, 3, 4, 5, … Б) – 10, - 8, - 6, - 4, … В) 0,3; 5,3; 10,3; 15,3; … Наведіть свій приклад арифметичної прогресії

Формула n – го члена арифметичної прогресії Нехай перший член арифметичної прогресії а1, і d – різниця. Тоді за означенням арифметичної прогресії : а2 = а1 + d; а3 = а2 + d = ( а1 + d ) + d = а1 + 2d; а4 = а3 + d = ( а1 + 2d ) + d = а1 + 3d; а5 = а4 + d = ( а1 + 3d ) + d = а1 + 4d і т. д. Помічаємо, що у цих формулах коефіцієнт при d на 1 менший від порядкового номера члена прогресії. Отже, можна записати: аn = а1 + ( n -1 ) d - а це і є формула п-го члена арифметичної прогресії, де аn – п-й член арифметичної прогресії, а1 – перший член арифметичної прогресії, n – порядковий номер, d – різниця. Наприклад: Знайти 5-й, 7-й та 10-й члени арифметичної прогресії, якщо перший член (а1) дорівнює 5, а різниця (d) дорівнює 4.

Наприклад: Знайти 5-й, 7-й та 10-й члени арифметичної прогресії, якщо перший член (а1) дорівнює 5, а різниця (d) дорівнює 4. Підказка: аn = а1 + ( n -1 ) d  

Властивості арифметичної прогресії:  

Робота в парах  

Девіз: „Один розум добре, а декілька - краще" Застосування формули n – го члена для … Клас об’єднується в групи. Над опрацюванням питань групи працюють 5-7 хв. 1 група: Застосування формули n – го члена для знаходження довільного її члена. 2 група: Застосування формули n – го члена для знаходження її першого члена. 3 група: Застосування формули n – го члена для знаходження різниці арифметичної прогресії. 4 група: Застосування формули n – го члена для знаходження порядкового номера її члена. Виконане завдання оцінюється в 4 бали.

1 група: Застосування формули n – го члена для знаходження довільного її члена Завдання: Знайти вісімнадцятий член арифметичної прогресії: 1; 1,3; 1,6;…

2 група: Застосування формули n – го члена для знаходження її першого члена Завдання: Знайти перший член арифметичної прогресії, якщо її різниця дорівнює 0,5, а дев’ятий член 3.

3 група: Застосування формули n – го члена для знаходження різниці арифметичної прогресії Завдання: Знайти різницю арифметичної прогресії ( аn ), у якій а1 = 28, а15 = - 21.

4 група: Застосування формули n – го члена для знаходження порядкового номера її члена  

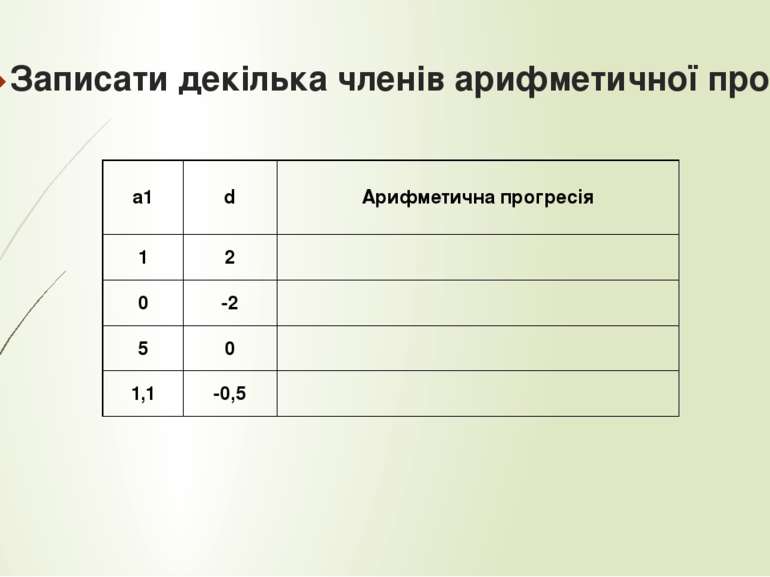
Записати декілька членів арифметичної прогресії а1 d Арифметична прогресія 1 2   0 -2   5 0   1,1 -0,5  

Робота з підручником № 687 ( а ) (ст. 174) № 692 № 716 (ст. 178) № 687 ( а ) (ст. 174) Розв’язання: а2 = (- 5 – 18) : 2 = - 11,5 № 692 Розв’язання: а2 = (- 5 – 11) : 2 = - 8

Сторінками історії математики Перший підручник “ Арифметика” Магницкого (кінець 18 ст.). Задача: “ Хтось продавав коня. Просив за нього 25 рублів. Купець, що побажав купити, обурився, що дорого. “Добре, - відповів продавець. Бери коня даром, а заплати тільки за цвяхи на його підковах. А цвяхів у всякій підкові 6 штук. І будеш ти мені платити за них у такий спосіб: за перший цвях 10 копійок, за другий цвях 20 копійок, за третій – 30 копійок і т.д.” Купець же, думаючи, що заплатить набагато менше, чим 25 рублів, погодився. Чи проторгувався купець, і якщо так, то на скільки?”  

Використання арифметичної прогресії поза уроками математики

« Сім чудес світу» Єгипетські піраміди. Піраміда складена з ретельно оброблених і щільно підігнаних вапнякових блоків вагою від 7 до 30 тонн. Причому кожен наступний є легшим за попередній на 0,0001 тонн. Скільки блоків треба було для спорудження цієї піраміди?  

Домашнє завдання: Опрацювати § 22, 23 Розв’язати № 690, № 710, № 718

Сьогодні на уроці я… Навчився (навчилася)… Зміг (змогла)… Мені не вдалося… Вдома потрібно… Дякую за увагу!