Презентація на тему:
Формули скорочення множення. Розкладання многочленів на множники

УРОК АЛГЕБРИ В 7 КЛАСІ Тема: Формули скорочення множення. Розкладання многочленів на множники. Котолуп Л.М., учитель математики МЗШ №11

ГРА «ЩАСЛИВИЙ ВИПАДОК” Гра “Щасливий випадок” проводиться на підсумкових уроках – систематизації та корекції знань. Більшість учнів переконані, що коли тему вивчили, то повторювати та систематизувати свої знання немає потреби; все одно нового нічого не дізнаються. Урок у формі гри істотно змінює ставлення учнів до математики. Гра відкриває можливість одночасно традиційно повторити вивчений матеріал та ознайомити з новими цікавими фактами чи то історичними, чи то сучасного характеру. Захоплюючись командною грою, учні прагнуть до перемоги, яка можлива лише за плідної розумової праці.

Мета: систематизувати та узагальнити знання, уміння і навички учнів з тем: “Формули скороченого множення”; “Розкладання многочленів на множники способом винесення спільного множника за дужки”; “Розкладання многочленів на множники способом групування” поглибити знання учнів з історії математики; розвити логічне мислення учнів; розвити математичну мову; виховувати інтерес до навчання, до математики; виховувати самооцінку.

Очікувані результати У процесі уроку учні зможуть: повторити основний теоретичний матеріал з теми; удосконалити свої вміння та навики з розкладання многочленів на множники; поглибити свої знання історичним матеріалом; розвити техніку обчислення.

ОБЛАДНАННЯ: картки з вправами; “замороки з бочки” картки з завданням.

ЕПІГРАФ У математиків існує своя мова – це формула. С. В. Ковалевська.

ПЛАН ПРОВЕДЕННЯ УРОКУ Організаційна частина. Організаційна частина. Основна частина. Проведення гри. Підбиття підсумків уроку та пояснення домашнього завдання.

1. Організаційна частина Повідомлення теми та завдання уроку. І сурова, й солов'їна Математики країна. Праця тут іде завзята Вмій лиш спритно рахувати. Повідомляється тема і завдання уроку.

2. Організаційна частина Клас поділяється на дві команди. Команди вибирають капітанів. Учитель в ролі ведучого. Він ставить запитання та веде підрахунок балів. Команди змагаються під девізом (назву команди і девіз вибирають самі). Гра складається з 6 частин: 1 гейм “Хто більше” 2 гейм “Замороки з бочки” 3 гейм “Ти мені – я тобі” 4 гейм “Сюрпризи із конверта” 5 гейм “Математичні софізми” 6 гейм “Гонка за лідером”

3. Основна частина. Проведення гри. 1 гейм “ХТО БІЛЬШЕ” Правильна відповідь оцінюється в один бал.

ЗАПИТАННЯ ДЛЯ ПЕРШОЇ КОМАНДИ: Що означає розкласти “многочлен на множники”? Як можна розкласти на множники многочлен: ах+ау? Чому дорівнює квадрат суми двох виразів? Якому тричлену тотожно дорівнює вираз: (а+х)2? Піднесіть до квадрата двочлен 1-х. Чи може бути від'ємним числом квадрат різниці двох чисел? Які способи розкладання на множники многочленів ви знаєте? Н які множники розкладається вираз: а2-2ас+с2? Чому дорівнює куб суми двох виразів? Розкладання многочленів на множники – це перетворення, обернене до………

ЗАПИТАННЯ ДЛЯ ДРУГОЇ КОМАНДИ: Які вирази називають многочленами? Назвіть найважливіші способи розкладання многочленів на множники. Чому дорівнює квадрат різниці двох чисел? Піднесіть до квадрата: а-2. З якого закону дій впливає спосіб розкладання многочлена на множники винесенням спільного множника за дужки? Чи може бути від'ємним числом різниця квадратів двох чисел? Чому дорівнює різниця квадратів двох чисел? Якому тричлену дорівнює: (а+у)2? На які множники розкладається вираз: а2+2ас+с2? Чому дорівнює куб різниці двох виразів?

Підведення підсумків першого гейму. (Команда супротивників також веде підрахунок балів).

2 гейм “ЗАМОРОКИ З БОЧКИ” Команди по черзі витягують листок з питанням з бочки і дають відповідь. За правильну відповідь нараховується два бали.

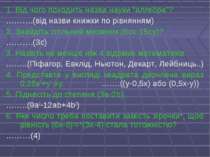
1. Від чого походить назва науки “алгебра”? ……….(від назви книжки по рівнянням) 2. Знайдіть спільний множник (6сх-15су)? ……….(3с) 3. Назвіть не менше ніж 4 відомих математиків. ……..(Піфагор, Евклід, Ньютон, Декарт, Лейбниць..) 4. Представте у вигляді квадрата двочлена вираз 0,25х2+у2-ху. …….((у-0,5х) або (0,5х-у)) 5. Піднесіть до степеня (3а-2b). ……..(9а2-12аb+4b2) 6. Яке число треба поставити замість зірочки*, щоб рівність (6х-8)2=*(3х-4)2 стала тотожністю? ………(4)

Підведення підсумків другого гейму.

3 гейм “ТИ МЕНІ – Я ТОБІ” Проспівати рядок пісні, в якому зустрічаються числа. За один рядок пісні – два бали.

4 гейм “СЮРПРИЗ ІЗ КОНВЕРТА” Кожній команді дається конверт із завданням та листи контролю. Капітани виходять розв’язувати вправи до дошки, інші учні розв’язують на місцях, а відповіді заносять до листа контролю. За правильну відповідь – один бал.

ЗАВДАННЯ ДЛЯ ПЕРШОЇ КОМАНДИ: Розкладіть на множники вирази: 5a+5b+ab+b2; …….(a+b)(5+b) х-3ху-21у+7; …….(х+7)(1-3у) Винесіть спільний множник за дужки: 12а3-18а2; …….(6a2(2а+3)) 60а2b2+36a3b6-48a3b2; …(12a3b2(5аb3+3b4-4) Розв'яжіть рівняння: х2-25=0; …….(х=5 чи х=-5) а2-6а+9=0; …….(а=3)

ЗАВДАННЯ ДЛЯ ДРУГОЇ КОМАНДИ: Розкладіть на множники вирази: a2+ax+xy+ay; …….((a+х)(а+у)) 5а-10-2с+ас; …….((а-2)(5+с)) Винесіть спільний множник за дужки: 15у3+20у4; …….(5у3(3+4у)) 10р4с6-15р2с2-20р3с4; …(5р2с2(2р2с4-3-4рс2) Розв'яжіть рівняння: 36-у2=0; …….(у=6 чи у=-6) х2+4х+4=0; …….(х=-2)

Підведення підсумків четвертого гейму.

5 гейм “МАТЕМАТИЧНІ СОФІЗМИ” Софізмом називають навмисно хибне твердження, яке має видимість правильності. Який би не був софізм, він обов’язково має одну або декілька замаскованих помилок. І.П.Павлов казав, що «правильно зрозуміла помилка – це шлях до відкриття».

Чим корисні софізми для вивчаючих математику? Що вони можуть дати? Розбір софізмів перш за все розвиває логічне мислення, прививає навички правильного мислення. Знайти помилку в софізмі – це значить освідомити її, а освідомлення помилки запобігає від повторення її в других математичних викладках. Математичні софізм привчають уважно і насторожено просуватися уперед, слідкувати за точністю формуліровок, правильністю записів і креслень, за законністю виконаних операцію Розбір софізмів допомогою засвоєнню вивченого матеріалу, розвиває вдумливість, критичне відношення до того що вивчається.

Розберемо знаменитий софізм 2 х 2 = 5. 1) Знайдемо помилку в наступних висловлюваннях. Маємо числову рівність (вірну) 4:4=5:5. Винесемо за дужки в кожній частині його спільний множник. Маємо: 4(1:1)=5(1:1). Числа в дужках рівні, тому 4=5, або 2х2=5. 2) 2х2=5, 4=5. Позначимо: 4=а, 5=b, (a+b):2=d. Маємо: а=2d-b; 2d-a=b. Перемножимо дві останні рівності по частинам. 2da-a2=2db-b2. Обидві частини отриманої рівності помножимо на -1 і додамо до результатів d2. Будемо мати: a2-2ad+d2=b2-2bd+d2, (a-d)2=(b-d)2, звідки Iа-dI=Ib-dI, маємо a=b і 2х2=5. Де допущена помилка?

6 гейм “ГОНКА ЗА ЛІДЕРОМ” Командам дається по три завдання. За кожну правильну відповідь нараховується один бал.

ЗАПИТАННЯ ДЛЯ ПЕРШОЇ КОМАНДИ: Малюнок. а2 ab ab b2

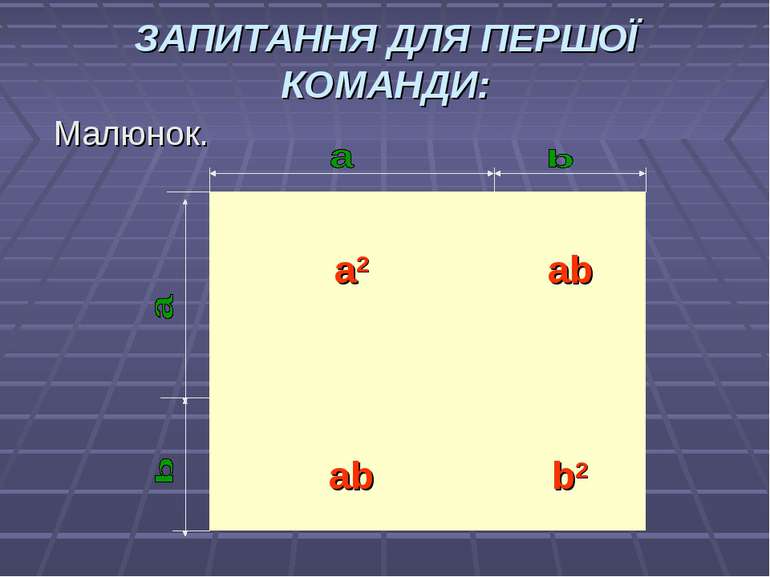
1.За допомогою малюнка стародавні греки доводили геометрично яку формулу? Поясніть. …………..(квадрат суми двох чисел). 2.Чи можна у формулу різниці квадратів замість змінних підставити будь-які числа, одночлени чи многочлени? 3. Доведіть, що 1617+1616 ділиться на 17.

ЗАПИТАННЯ ДЛЯ ДРУГОЇ КОМАНДИ: Малюнок a2 – b2 (a+b)(a-b)

1.Цей малюнок є ілюстрацією якої формули? Поясніть. ……………….……..(різниці квадратів). 2.При яких значеннях а і b рівність (a-b)2=(a+b)2 правильна? 3. Доведіть, що 512+510 ділиться на 13.

Підбиття підсумків гри.

Підбиття підсумків уроку та пояснення домашнього завдання. 1. Самооцінка учнів. 1). Чи знав відповідь на поставленні запитання? Так. Ні. Не зовсім. 2) Чи приніс команді бали? Так. Ні. Не зовсім. 3) Чи зміг висунути свою пропозицію? Так. Ні. Не зовсім. 4) Чи досяг мети на уроці? Так. Ні. Не зовсім. 5) Чи дізнався для себе щось нове? Так. Ні. Не зовсім. 2. Повторити п. 15-18, підготуватися до контрольної роботи. Сторінка 147 – розв'язати варіант 1 самостійної роботи за підручником.

Дякуємо за увагу!