Презентація на тему:
”Розробка наукових засад створення систем підтримки прийняття рішень ординального типу”

Тема НДР ”Розробка наукових засад створення систем підтримки прийняття рішень ординального типу” шифр: "Ранги“ (2009-2011) Науковий керівник: зав. лабораторії, к.т.н., с.н.с. В.В.Циганок Виконавці: с.н.с., к.т.н., доцент П.Т.Качанов с.н.с., к.т.н. С.В.Каденко м.н.с. О.В.Андрійчук пров.інж.Г.А.Гоменюк Об’єкт дослідження – системи підтримки прийняття рішень (СППР), у базах знань яких використовуються ординальні експертні оцінки Мета роботи – підвищення ступеня адекватності експертних рішень за рахунок розширення можливостей наявних та нових СППР шляхом розробки принципів побудови СППР нового класу Головна задача дослідження – розробка методів, які є основою для створення СППР ординального типу

Приклади застосування експертних СППР у світі Енергетика Application of Analytic Hierarchy Process To Determining A Priori Distribution of Error-Free Running Time For High-Reliability Components Bochkov, Alexander V. (Застосування методу аналізу ієрархій для визначення апріорного розподілу часу безперебійної роботи високонадійних компонентів газового обладнання) – Proceedings of ISAHP 2009 – http://isahp.org . Analysis and Evaluation of Technological and Operational Alternatives for Heavy Oil Gathering Systems in the Fields of Castilla and Chichimene, Colombia, Castillo, Mario (Аналіз та оцінка технологічних та операційних альтернатив для систем видобутку важкої нафти у Колумбії) – Proceedings of ISAHP 2009 – http://isahp.org . Full Cost Account for Integrated Energy Resources Planning Using the Analytic Hierarchy Process Decio Cicone Junior, Pascoal Henrique da Costa Rigolin, Miguel Edgar Morales Udaeta, Jose Aquiles Baesso Grimoni (Повне урахування витрат на інтегрований розподіл енергоресурсів за допомогою методу аналізу ієрархій) – Proceedings of ISAHP 2011 – http://isahp.org

Приклади застосування експертних СППР у світі Промисловість Using AHP and ANP to Evaluate the Relation Between Reverse Logistics and Corporate Performance in Brazilian Automotive Industry Marins, Fernando Augusto Silva (Застосування методів аналізу ієрархій та мереж при оцінці зворотної логістики та корпоративної продуктивності у автомобільній промисловості Бразилії) Proceedings of ISAHP 2009 – http://isahp.org Using ELECTRE and MACBETH MCDA methods in an industrial performance improvement context, Vincent Civille, Lamia Berrah, Gilles Mauris, pp. 162-169 (Застосування методів ELECTRE та MACBETH у контексті підвищення продуктивності промисловості (Франція)) / Extended abstracts of OR52, pp. 162-169, 2010. Prioritization of New Product Development Activities for Electronics Manufacturing – Eduardo Gomes Salgado, Valerio A. P. Solomon, Carlos Henrique Pereira Mello (Визначення пріоритетності заходів з розробки нової продукції у виробництві електроніки) - Proceedings of ISAHP 2011 – http://isahp.org

Приклади застосування експертних СППР у світі Комерційна (ділова) сфера A Fuzzy MCDM Approach for Evaluating Corporate Image and Reputation in the Airline Market Liou, J.H. (Нечіткий підхід до мультикритеріцальної підтримки прийняття рішень для оцінки іміджу та репутації корпорації на ринку авіаперевезень) - Proceedings of ISAHP 2009 - http://isahp.org The Analytic Hierarchy Process in the Supplier Selection Problem Genovese, Andrea (Застосування Методу Аналізу Ієрархій при вирішенні задачі вибору поставщиків) - Proceedings of ISAHP 2009 - http://isahp.org Analytic Network Process as Qualitative Simulating Tool: Researching of Financial Crisis Andreichicova, Olga (Метод аналізу мереж як інструмент якісного моделювання: дослідження фінансової кризи) - Proceedings of ISAHP 2009 – http://isahp.org Applications of Multi-criteria Decision Analysis in the Selection of Foreign Markets to Export – Angela Reyes, Diana Lesmes, Mario Castillo (Застосування багатокритеріального аналізу варіантів рішень для вибору зарубіжних ринків експорту) - Proceedings of ISAHP 2011 - http://isahp.org

Приклади застосування експертних СППР у світі Банківська галузь Banking Crime Analysis and the Effectiveness of Banking Supervision: Combining Game Theory and the Analytical Network Process Approach Abdullah, Piter (Аналіз злочинів у банківській сфері за допомогою комбінованого підходу, що поєднує теорію ігор та метод аналізу мереж (Індонезія)) – Proceedings of ISAHP 2009 – http://isahp.org Analysis of the Efficiency of Banks in Montenegro Using the AHP Dragasevic, Zdenka (Аналіз ефективності діяльності банків у Чорногорії за допомогою методу аналізу ієрархій) – Proceedings of ISAHP 2009 – http://isahp.org Appreciation of Rupiah: Benefits, Costs, Opportunities and Risks Analysis - Abdullah Piter (Оцінка рупії: аналіз вигід, втрат, можливостей та ризиків (Індія) ) - Proceedings of ISAHP 2011 – http://isahp.org

Приклади застосування експертних СППР у світі Транспортна сфера Applying AHP to the Prioritization of Maritime Booking Confirmation Becker, Joao Luiz (Застосування методу аналізу ієрархій для визначення пріоритетів підчас виділення засобів для морського транспортування вантажів) Proceedings of ISAHP 2009 – http://isahp.org Multi-Actor, Multi-Criteria Analysis (MAMCA) for transport project appraisal, Cathy Macharis, (Мультиагентний багатокритеріальний аналіз при оцінці проектів у транспортній галузі) / Extended abstracts of OR52, pp. 98-105, 2010. Public Parking Locating with Multi Criteria Decision Making Methods (MCDM) (Case Study: Old Market District of Urmia City) (Вибір розміщення громадської стоянки автотранспорту із застосуванням методів багатокритеріальної підтримки прийняття рішень. На прикладі району Старого Ринку в місті Урміа (Пакістан)) / Land Use Policy – http://ees.elsevier.com/lup/

Приклади застосування експертних СППР у світі Сталий розвиток Multicriteria analysis of policy options scenarios to reduce the aviation climate impact – an application of the PROMETHEE based D-Sight software, Annalia Bernardini, Quantin Hayez, Cathy Macharis, Yves De Smet, (Багатокритеріальний аналіз можливих сценаріїв для зменшення впливів авіаційної галузі на зміну клімату – застосування програми D-Sight на базі методу PROMETHEE) Extended abstracts of OR52, pp. 148-157, 2010. Using ANP for the Selection of Green Supply Chain Management Strategies Chen, Chiau-Ching (Вибір стратегій для екологічно сталого управління каналом поставок підприємств електронної промисловості) Proceedings of ISAHP 2009 – http://isahp.org A Comparative Analysis Based on Analytic Network Process for Selection of a Mini Wind Station Plant - Graziella Aghilone, Fabio De Felice, Antonella Petrillo (Порівняльний аналіз варіантів вітряних електростанцій на основі методу аналізу мереж) - Proceedings of ISAHP 2011 – http://isahp.org

Приклади застосування експертних СППР у світі Автоматизація та інформатизація Design of a Methodology for Identifying and Selecting the Best Alternative in Acquiring the Information System for a Company Castillo, Mario (Створення методології для вибору найкращої альтернативи підчас придбання інформаційної системи для компанії) - Proceedings of ISAHP 2009 – http://isahp.org Application of a multi-criteria decision model for the selction of the best sales force automatization technology alternative for a Colombian enterprise, I. Cortina, N. Granados, M. Castillo, (Застосування багатокритеріальної моделі прийняття рішень для вибору найкращого способу автоматизації сфери продажу для колумбійського підприємства) / Extended abstracts of OR52, pp. 169-177, 2010. Alpha-cut Fuzzy Analytic Network Process Based Approach to Evaluate Simulation Software Packages – Zeki Aya, Ahmet Deniz Yucekaya (Підхід до оцінки симуляційних пакетів програмного забезпечення на основі альфа-зрізіу у нечіткому методі аналізу мереж) - Proceedings of ISAHP 2011 – http://isahp.org

Приклади застосування експертних СППР у світі Управління The use of MCDA in strategy and change management, William Mayon-White, Ayleen Wisudha, (Застосування багатокритеріальної підтримки прийняття рішень для розробки стратегій та управління змінами) / Extended abstracts of OR52, pp. 105-108, 2010. Prioritizing the Nine Challenges of Malaysian Vision 2020 – Rafikul Islam (Розстановка пріоритетів серед дев’яти основних проблем перспективного розвитку Малайзії до 2020 року) - Proceedings of ISAHP 2011 – http://isahp.org Кадрові рішення Investigation into the Application of Multiple Criteria Decision Making for an Online Candidate Short Listing System Peiris, PathiranagePadmaliManesha (Дослідження застосування мультикритеріальної підтримки прийняття рішень у системі відбору кандидатів у мережі) Proceedings of ISAHP 2009 – http://isahp.org A Contemporary Method of Employees Assessment, Wiktor Adamus - (Сучасний метод оцінки персоналу) – Proceedings of ISAHP 2011 – http://isahp.org

Тема НДР ”Розробка наукових засад створення систем підтримки прийняття рішень ординального типу” шифр: "Ранги“ (2009-2011) 1 етап.  Розробка методів оцінки компетентності джерел інформації (01.2009-06.2009) 2 етап.  Розробка методів визначення порогових значень коефіцієнтів узгодженості (коефіцієнта рангової кореляції та коефіцієнта конкордації) і умов достатності цих коефіцієнтів (07.2009‑12.2009) 3 етап. Розробка методів врахування компетентності джерел інформації при визначенні групового ранжирування. (01.2010-06.2010) 4 етап. Розробка методів визначення групового ранжирування із зворотнім зв'язком з експертами. Дослідження явища реверсу рангів. (07.2010- 12.2010) 5 етап. Розробка методів визначення ваг часткових ранжирувань по множині сумарних ранжирувань. (01.2011-06.2011) 6 етап. Розробка структурної схеми і алгоритму функціонування системи підтримки прийняття рішень на основі використання ординальних оцінок. (07.2011-12.2011)

1 етап. Розробка методів оцінки компетентності джерел інформації (01.2009-06.2009) Очікувані результати: Методи та алгоритми їхньої реалізації.

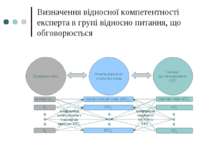
Визначення відносної компетентності експерта в групі відносно питання, що обговорюється Експертна група експерт (Е)1 Е2 Еk Питання, що обговорюється (ОП) ключове слово (КС)1 КС2 КСn Область діяльності експертної групи базове ключове слово (БКС)1 БКС2 БКСm коефіцієнти подібності КС ОП із БКС коефіцієнти компетентності експертів відносно БКС

Наукові основи методу При визначенні коефіцієнтів з отриманих експертним шляхом рангів пропонується застосовувати закон Бенфорда: pr= logn-1(1 + 1/r) Для визначення відносного коефіцієнта компетентності члена групи в ОП пропонується використовувати функцію виду коефіцієнти компетентності експертів відносно кожного БКС визначаються по трьох компонентах: самооцінка, взаємооцінка та об'єктивна складова Самооцінка: для визначення відносної повноти знань стосовно кожного БКС експертові пропонується проранжирувати БКС у порядку зниження повноти своїх знань відносно БКС Взаємооцінка: кожний експерт ранжирує БКС колег, методом Борда знаходиться результуючі ранжирування Об'єктивний компонент визначається в декілька етапів. Спочатку формується множина критеріїв, що відображають компетентність експерта щодо категорії, яку визначає БКС, і допускають документальні підтвердження його досягнень. Потім цим критеріям привласнюються відповідні ваги, що відображають відносну значимість критеріїв. Далі експерти оцінюються за критеріями, на основі чого розраховуються результуючі оцінки їхньої компетентності.

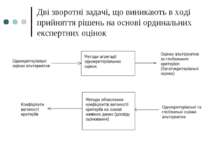
Визначення відносної компетентності кандидатів у члени експертних комісій, на основі досвіду роботи попередньої комісії Дано: Експертна комісія/група, створена для вирішення конкретного класу задач, тобто множина експертів E1, E2, …, Em. Множина показників (незалежних за перевагами критеріїв), що відображають різні складові показника компетентності членів комісії: C1, C2, …, Cn. G – загальний (глобальний) показник компетентності експерта. Строге ранжирування експертів за рівнем компетентності G: g1, …, gm. Множина ординальних оцінок експертів за окремими складовими показника компетентності, тобто за критеріями її оцінки: {rij}, де rij – ранг (ординальна оцінка компетентності) i-го експерта за j-м критерієм. Множина кандидатів у члени комісії Em+1, Em+2, …, Em+p. Треба знайти: Коефіцієнти вагомості локальних критеріїв оцінки компетентності експертів {wj}, j=1..n; wj>0; ∑wj=1, які б дозволяли зберегти глобальне ранжирування альтернатив при зваженому сумуванні їхніх однокритеріальних ординальних оцінок. Ранжирування кандидатів за загальним (глобальним) показником компетентності G: gm+1, …, gm+p.

Визначення відносної компетентності кандидатів у члени експертних комісій, на основі досвіду роботи попередньої комісії Ідея розв’язання За апріорним припущенням, глобальне ранжирування експертів (наявних та нових) будується як ранжирування зважених сум їхніх однокритеріальних рангів, тому задача зводиться до пошуку області розв’язків системи нерівностей наступного виду: де (вважаємо, що експертів у ранжируванні пересортовано у порядку спадання їхніх глобальних рангів). Після того як буде знайдено область допустимих значень коефіцієнтів вагомості критеріїв, тобто її крайні точки та центр можна шляхом анкетування, чи об’єктивного дослідження побудувати ранжирування кандидатів у члени комісії за локальними складовими глобального показника компетентності: де rm+i,j – ранг (ординальна оцінка компетентності) i-го кандидата за j-м критерієм. Потім, підставивши у формулу зваженої суми щойно обчислені ваги локальних критеріїв оцінки компетентності експертів можна побудувати ранжирування кандидатів у члени комісії за глобальним критерієм. Це буде ранжирування зважених сум їхніх ординальних оцінок за локальними складовими показника компетентності:

2 етап. Розробка методів визначення порогових значень коефіцієнтів узгодженості (коефіцієнта рангової кореляції та коефіцієнта конкордації) і умов достатності цих коефіцієнтів (07.2009‑12.2009) Очікувані результати: Методи та алгоритми їхньої реалізації.

Розроблено метод обчислення коефіцієнта конкордації з урахуванням компетентності експертів Сутність підходу полягає у виборі найбільшого спільного дільника для значень коефіцієнтів компетентності експертів, що виконали ранжирування. Коефіцієнти приводяться до чисел з натурального ряду, після цього розглядаються ранжирування кожного експерта, як множина однакових ранжирувань рівно-компетентних експертів. Коефіцієнт конкордації w множини індивідуальних ранжирувань n альтернатив, виконаних m рівно-компетентними експертами, визначається виразом: w=12 S / m2(n3-n), де S - сума квадратів відхилень сум рангів альтернатив від їхнього (сум рангів альтернатив) середнього значення. З урахуванням вищезгаданого підходу одержуємо коефіцієнт конкордації з урахуванням компетентності експертів:

Визначення граничних (порогових) значень коефіцієнта конкордації Скористаємося підходом до визначення граничних значень коефіцієнта узгодженості множини кардинальних оцінок. Згідно з ним визначаються два граничних значення. Перше, назване порогом виявлення To, визначає умови наявності корисної інформації в множині експертних оцінок. Перевищення другого граничного значення, названого порогом застосування Tu, означає достатню з погляду особи, що приймає рішення, точність результуючого групового ранжирування. В якості порогів виявлення й застосування використовуються коефіцієнти узгодженості спеціальним чином побудованих множин ординальних експертних оцінок. Виведено формулу обчислення порогу виявлення: Tо=w0=24/m2(n3-n). Цей поріг обчислено, як коефіцієнт конкордації m повністю неузгоджених ранжирувань n об'єктів , в яких довільно виконано одну перестановку сусідніх об'єктів, і таким чином, обумовлено наявність корисної інформації. Зроблено висновок, що для того, щоб результуюче ранжирування збігалося з тим, що обчислено по повністю узгодженій множині ранжирувань, відстань l між кожним ранжируванням при формуванні множини та вихідним ранжируванням ri повинна задовольняти умові Виходячи з цього висновку, порогом застосування Tu множини m індивідуальних ранжирувань n об'єктів будемо вважати значення коефіцієнта конкордації множини m ранжирувань, що відрізняються від множини повністю узгоджених ранжирувань не більше ніж на m / 2 (значення Tu не залежить від конкретного виду ранжирування, а визначається тільки величинами заданої відстані l та кількості ранжирувань/експертів m).

Визначення граничних значень коефіцієнта рангової кореляції Відомо, що для визначення коефіцієнта рангової кореляції двох строгих ранжирувань доцільно представити індивідуальні ранжирування у вигляді матриць, визначених у такий спосіб: 1, якщо ah перевершує au; dhu= -1, якщо au перевершує ah. При цьому коефіцієнт рангової кореляції визначається виразом: n n = ( dhui dhu j) / n (n-1), h=1 u=1 де dhui, dhu j - елементи матриць, що задають індивідуальні ранжирування ri та rj відповідно. Неважко бачити, що для пари (ri0 ,rj0 ) повністю неузгоджених індивідуальних ранжирувань всі добутки dhuidhuj рівні -1, тому для цієї пари =-1. Очевидно, що мінімальна відмінність пари (ri ,rj ) від пари (ri0 ,rj0 ) повністю неузгоджених індивідуальних ранжирувань буде мати місце, якщо в одному з ранжирувань ri0 або rj0 поміняти місцями дві альтернативи. При цьому два добутки dhuidhuj поміняють знак, внаслідок чого, як випливає з попереднього виразу, T0= = [4/n(n-1)]-1. В якості порогу застосування Tu приймемо коефіцієнт рангової кореляції пари ранжирувань (riu ,rju ), що відрізняється від повністю узгодженої пари ранжирувань (ri1 ,rj1 ) рангами u пар альтернатив (при u≤]m/2[, де кількість ранжирувань m=2, і тому u≤1, результуюче ранжирування, обраховане методом Борда, не буде відрізнятись від ранжирування, отриманого від повністю узгодженої пари ранжирувань (ri1 ,rj1 )). Зі способу побудови матриць, що задають індивідуальні ранжирування випливає, що якщо індивідуальне ранжирування відрізняється від повністю узгодженого рангами u пар альтернатив, то 2u добутків dhuidhuj поміняють знак, внаслідок чого, як випливає з формули обрахування : Tu= 1-4u/n(n-1) = 1-[4/n(n-1)].

3 етап. Розробка методів врахування компетентності джерел інформації при визначенні групового ранжирування (01.2010-06.2010) Очікувані результати: Методи та алгоритми їхньої реалізації

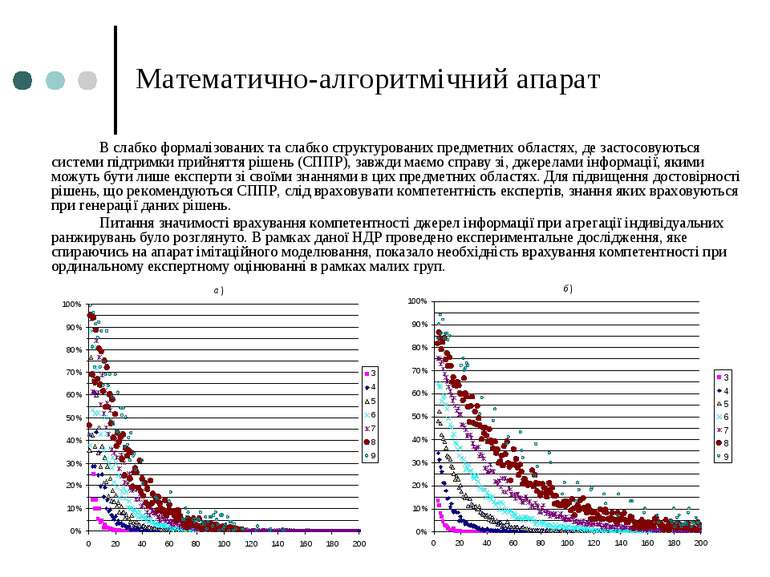
Математично-алгоритмічний апарат В слабко формалізованих та слабко структурованих предметних областях, де застосовуються системи підтримки прийняття рішень (СППР), завжди маємо справу зі, джерелами інформації, якими можуть бути лише експерти зі своїми знаннями в цих предметних областях. Для підвищення достовірності рішень, що рекомендуються СППР, слід враховувати компетентність експертів, знання яких враховуються при генерації даних рішень. Питання значимості врахування компетентності джерел інформації при агрегації індивідуальних ранжирувань було розглянуто. В рамках даної НДР проведено експериментальне дослідження, яке спираючись на апарат імітаційного моделювання, показало необхідність врахування компетентності при ординальному експертному оцінюванні в рамках малих груп.

Сутність підходу Пропонується в методах визначення узагальнених ранжирувань для малих експертних груп застосовувати підхід заснований на визначенні множин, еквівалентних заданій множині ранжирувань, даних рівно-компетентними експертами. Сутність підходу Задача формулюється в такий спосіб. Дано: множину експертів; множину нормованих коефіцієнтів відносної компетентності експертів; множину індивідуальних ранжирувань альтернатив . Потрібно визначити групове ранжирування . Коефіцієнти компетентності попередньо приведемо до значень з натурального ряду: . Виберемо найбільший спільний дільник для коефіцієнтів компетентності . Тоді для кожного можна представити у вигляді , де – ціле число. Число можна розглядати як кількість експертів з рівною компетентністю , у сукупності еквівалентних експертові з компетентністю . Тому множину індивідуальних ранжирувань альтернатив можна замінити множиною ранжирувань, у якій замість одного ранжирування записано його копій. При цьому задача визначення групового ранжирування з m експертами різної компетентності зводиться до задачі визначення групового ранжирування з рівно-компетентними експертами, кожний з яких має коефіцієнт компетентності . В подальшому, використовуємо відомі методи агрегації ранжирувань рівно-компетентних експертів, наприклад, Кондорсе або Борда.

4 етап.  Розробка методів визначення групового ранжирування із зворотнім зв’язком з експертами. Дослідження явища реверсу рангів (07.2010-12.2010). Очікувані результати: Методи та алгоритми їхньої реалізації

Формальна постановка задачі про достатність рівня узгодженості множини ранжирувань та хід її рішення Дано: – множина із m індивідуальних експертних ранжирувань n об'єктів, тобто , де , – ранг j-го об'єкта в i-ому ранжируванні. Визначити:  чи достатній рівень узгодженості множини ранжирувань R(m) для побудови на її основі агрегованого ранжирування. Хід рішення:  1) Індивідуальні ранжирування r , i = (1,m) представляються у вигляді матриць відношень

хід рішення (продовження) 2) Підсумкова матриця відношення : містить множину елементарних групових рішень . Тобто, , якщо більшість із і , якщо більшість із . 3) Підсумкова матриця аналізується на предмет її несуперечливості:

Результати вирішення задачі Таким чином, у ході рішення ми доходимо висновку, що за умови t=0 досягається достатній рівень узгодженості множини ранжирувань R(m) , і на основі цієї множини можна будувати агреговане ранжирування. Для агрегації індивідуальних ранжирувань можна скористатися відомими методами. У випадку невиконання умови (при t>0) пропонується організувати зворотний зв'язок з експертами з метою приведення t до нуля. Показано, що при парних значеннях m може виникати ситуація, коли принцип більшості при формуванні елементів підсумкової матриці не виконується через паритет думок, тоді пропонується домагатися виконання цього принципу так само, за допомогою зворотного зв'язку з експертами.

Метод організації зворотного зв’язку з експертами для підвищення узгодженості їхніх суджень при груповому ординальному оцінюванні Передумови та застереження: Перед усім зазначимо, що підсумкове відношення будується у вигляді матриці домінування і, якщо ця матриця не є транзитивною, агрегація індивідуальних ранжирувань вважається неприпустимою, і потрібно звертатися до експертів із пропозицією змінити свої ранжирування альтернатив таким чином, щоб підсумкове відношення стало транзитивним. Додатковою умовою при організації зворотного зв'язку з експертами й агрегації індивідуальних ординальних експертних оцінок може бути, але це не є обов'язковим, одержання строгого підсумкового ранжирування. Така вимога може виникнути зі специфіки конкретної розв'язуваної задачі або ж, як наслідок, з постулату, що задані індивідуальні ранжирування теж є строгими. Крім того, важливо вказати, що застосування зворотного зв'язку не повинне чинити будь-який тиск на раніше висловлену думку експерта, і виконання цієї умови гарантується постійною наявністю для експерта вибору приймати пропозиції щодо зміни свого ранжирування, чи ні.

Постановка задачі та ідея рішення Постановка задачі Дано: Множина n альтернатив для експертного оцінювання; множина строгих ранжирувань цих альтернатив, виконаних m експертами; підсумкове відношення, у загальному випадку, не транзитивне, задане у вигляді матриці, побудованої шляхом агрегації індивідуальних ранжирувань за методом Кондорсе. Необхідно організувати зворотний зв'язок з експертами з метою перетворення підсумкового відношення в транзитивне, тобто, потрібно послідовно визначати, до кого саме із групи експертів потрібно звернутися, і які саме альтернативи запропонувати переставити в їхніх індивідуальних ранжируваннях. Критерієм якості зворотного зв'язку повинна бути мінімізація кількості звертань до експертів у процесі діалогу. Ідея методу рішення Оскільки кількість звертань до експертів із пропозиціями про зміну їхніх попередніх оцінок залежить від самих відповідей експертів (тобто від того, погоджується експерт на пропозицію, чи ні), то мінімізувати їхню кількість в класичному вигляді не вдається. У зв'язку із цим, пропонується, крім загальної кількості питань, що задаються, групі експертів у процесі діалогу, ураховувати також і ймовірність позитивних відповідей на задані питання. Адже специфіка зворотного зв'язку така, що негативні відповіді експертів у процесі діалогу (тобто їхні відмови змінити раніше висловлену думку) ведуть до наступного пошуку інших варіантів перетворення підсумкового відношення в транзитивне, і, тим самим, до нових пропозицій до експертів із приводу зміни їхніх вихідних ранжирувань.

Особливості застосування Генетичного алгоритму Однієї з особливостей ГА є його універсальність. Фактично, для реалізації будь-якої конкретної задачі пошуку екстремуму необхідно задати специфічну функцію корисності й здійснити кодування варіантів рішень із області можливих рішень. Функція корисності , де - відповідає індивідуальному ранжируванню, де n – кількість альтернатив у ранжируванні, h – менший із двох рангів альтернатив, що беруть участь у перестановці, d – відстань між альтернативами, що переставляються (абсолютне значення різниці рангів альтернатив, що переставляються: ). Кодування варіантів рішень Варіант рішення (у термінах притаманних еволюційним методам “особина”) в запропонованому варіанті алгоритму являє собою набір строгих ранжирувань експертів, результатом агрегації яких по методу Кондорсе є строге ранжирування, і до яких пропонується звести вихідний набір експертних ранжирувань. Для кожної такої особини є можливість однозначно обчислити функцію корисності. Пропонується, кожному можливому варіанту ранжирування n альтернатив поставити у взаємо-однозначну відповідність число з натурального ряду. Кількість чисел у такій множині буде дорівнює числу перестановок n елементів: Pn = n!. Операції “схрещування” та “мутації” Ці операції ГА мають свої особливості при реалізації даного варіанту методу. Випадковий вибір з отриманої множини ранжирувань, що належать шляхам перетворення одної з 2-х особин в іншу, дає ранжирування експерта, яке входить до складу множини ранжирувань, що утворюють результат операції «кросинговера» (особину, породжену схрещуванням). Для кожного ранжирування із множини (особини, обраної для мутації) пропонується здійснити з імовірністю, заданою, як вхідний параметр ГА (ймовірністю мутації) випадково обраних елементарних перестановок. Таким чином, при такому перетворенні з обраної для мутації множини ранжирувань потенційно може бути отримана множина, що складається з будь-яких із всіх можливих ранжирувань. Причому, ймовірність одержання в результаті мутації особини, «ближчої» за кількістю перестановок у ранжируваннях до вихідної особини, завжди більша ніж ймовірність одержання більш віддаленої особини.

Дослідження явища реверсу рангів Реверс рангів полягає у порушенні підсумкового ранжирування заданої множини альтернатив у випадку, коли до множини включається деяка нова альтернатива, або з неї виключається одна з наявних альтернатив. Приклад реверсу рангів: після додавання альтернативи A4 маємо: Індивідуальні ранжирування альтернатив 1-3 залишались ті ж самі, але в агрегованому ранжируванні альтернативи 2 і 3 одного рангу, а в попередньому вони були різних рангів. Тобто при додаванні 4-ї альтернативи виник реверс рангів між двома існуючими. Показано, що дане негативне явище зумовлене зміною множини співвідношень, що враховуються при аналізі множини альтернатив, має місце, і є цілком закономірним для ординальної шкали.

5 етап.  Розробка методів визначення ваг часткових ранжирувань по множині сумарних ранжирувань (01.2011-06.2011) Очікувані результати: Методи та алгоритми їхньої реалізації

Загальна постановка задачі Дано: Множина альтернатив . Множина незалежних по перевагах , сумісних між собою критеріїв оцінки альтернатив . (сумісними слід вважати такі два підкритерії глобального критерію, що збільшення оцінки альтернативи за одним критерієм не виключає збільшення оцінки альтернативи за іншим критерієм з пари. Якщо усі безпосередні підкритерії заданого критерію попарно сумісні, то множина підкритеріїв є сумісною). Ранжирування альтернатив за кожним з критеріїв ; rij – оцінка (ранг) i-ї альтернативи за j-м критерієм Строге підсумкове ранжирування (ранжирування альтернатив за глобальним критерієм G) Треба знайти нормовані коефіцієнти відносної вагомості критеріїв оцінки альтернатив ; які підчас агрегації (зваженого сумування) однокритеріальних ранжирувань альтернатив дозволяють зберегти задане підсумкове ранжирування альтернатив.

Запропоновані методи вирішення задачі Ітераційний метод настроювання вагових коефіцієнтів, ґрунтується на апараті ітераційного настроювання параметрів нейронних мереж, і дозволяє знайти розв’язок, що задовольняє умові задачі, або з’ясувати, що область її розв’язків порожня. Метод пошуку центру області допустимих значень вагових коефіцієнтів із зворотним зв’язком з експертом, зводиться до пошуку області розв’язків системи нерівностей, сформованої на основі обмежень, що випливають із заданих ранжирувань, і дозволяє визначати не єдиний довільний розв’язок, а всю область розв’язків, якщо вона не порожня. У випадку, коли області розв’язків не існує – пропонується, використовуючи зворотний зв’язок, звернутися до особи, яка будувала глобальне ранжирування, та запропонувати їй переставити альтернативи у ньому таким чином, щоб область існувала.

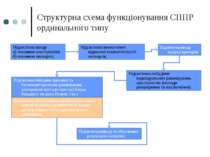
6 етап.  Розробка структурної схеми і алгоритму функціонування СППР на основі використання ординальних оцінок (07.2011-12.2011) Очікувані результати: Структурна схема та алгоритм функціонування СППР ординального типу

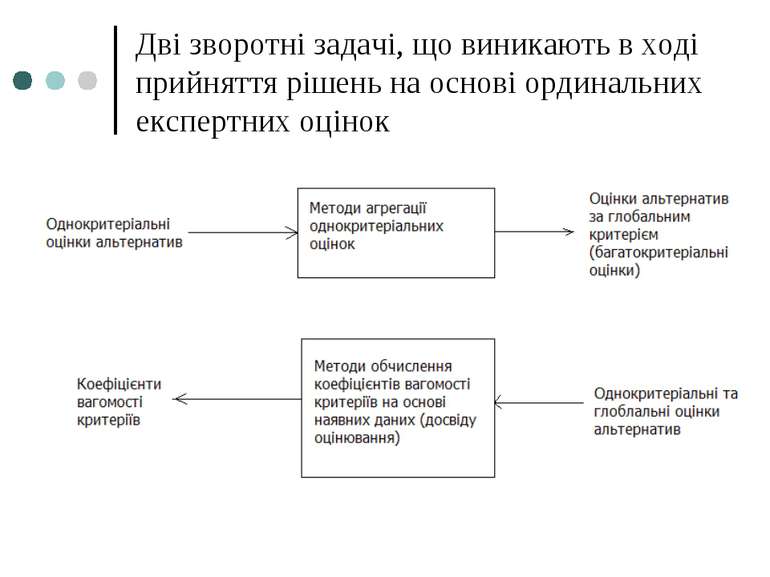
Дві зворотні задачі, що виникають в ході прийняття рішень на основі ординальних експертних оцінок

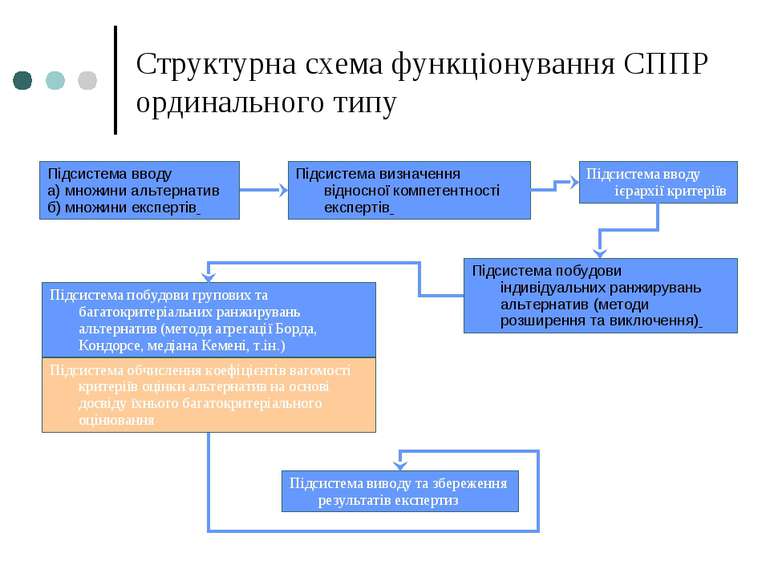
Структурна схема функціонування СППР ординального типу Підсистема вводу а) множини альтернатив б) множини експертів Підсистема визначення відносної компетентності експертів Підсистема побудови групових та багатокритеріальних ранжирувань альтернатив (методи агрегації Борда, Кондорсе, медіана Кемені, т.ін.) Підсистема побудови індивідуальних ранжирувань альтернатив (методи розширення та виключення) Підсистема вводу ієрархії критеріїв Підсистема виводу та збереження результатів експертиз Підсистема обчислення коефіцієнтів вагомості критеріїв оцінки альтернатив на основі досвіду їхнього багатокритеріального оцінювання

Висновки Розроблено методи, що є основою створення СППР ординального типу: методи оцінки компетентності джерел інформації, що базуються на ординальному експертному оцінюванню метод обчислення коефіцієнта конкордації з урахуванням компетентності експертів методи визначення граничних значень коефіцієнтів узгодженості (коефіцієнта конкордації та коефіцієнта рангової кореляції) методи врахування компетентності джерел інформації при визначенні групового ранжирування методи визначення групового ранжирування із зворотнім зв'язком з експертом, досліджено явище реверсу рангів методи, що дозволяють використовувати ординальні оцінки як джерело даних для визначення ваг (впливів) критеріїв, що входять до заданої ієрархії або мережі (визначення на основі досвіду ранжирування альтернатив за цими критеріями) запропоновано концепцію побудови СППР ординального типу та алгоритм її функціонування

Публікації Kadenko, Sergey Experience-Based Decision Support Methods using Ordinal Expert Estimates. Proceedings of the 10th International Symposium on the Analytic Hierarchy/Network Process. Multi-criteria Decision Making. Pittsburgh, PA, USA. 29/07 – 1/08/2009 // ISSN 1556-8296. Каденко С.В. Метод визначення коефіцієнтів відносної вагомості критеріїв на основі ординальних оцінок альтернатив, із зворотнім зв’язком // Системи підтримки прийняття рішень. Теорія і практика. // Збірник доповідей науково-практичної конференції з міжнародною участю // НАН України, Інститут проблем математичних машин і систем. – 2009. – с.39-42. Циганок В.В. Про одну стратегію організації зворотного зв’язку з експертами при груповому ординальному оцінюванні // Системи підтримки прийняття рішень. Теорія і практика // Збірник доповідей науково-практичної конференції з міжнародною участю. – Київ: НАН України, Інститут проблем математичних машин і систем. – 2010. – с.26-29. Tsyganok,Vitaliy A method for providing sufficient strict individual rankings’ consistency level while group decision-making with feedback // OR-52 Keynotes and Extended Abstracts, Operational Research Society Ltd., Royal Holloway University of London, UK 7 9/9/2010 // ISBN 0 903440 47 4, pp. 142-147. Kadenko, Sergey & Tsyganok, Vitaliy Decision-making Support System for Multi-criteria Personnel Evaluation // Special Session on Decision Making for Sustainability: Summer School 2010, Italy 4pages. Каденко С.В., Циганок В.В. Про один підхід до прийняття кадрових рішень. Реєстрація, зберігання і обробка даних. – 2009. – т.11. – №3.– с.66-74. Цыганок В.В., Каденко С.В. О достаточности степени согласованности групповых ординальных оценок. Проблемы управления и информатики. – 2010. – №4.– с.107-112. Kadenko,Sergey Personnel-related decision-making using ordinal expert estimates // OR-52 Keynotes and Extended Abstracts, Operational Research Society Ltd., Royal Holloway University of London, UK 7 9/9/2010 // ISBN 09034 40 474, pp. 177-183. Tsyganok V.V., Kadenko S.V. On Sufficiency of the Consistency Level of Group Ordinal Estimates. Journal of Automation and Information Sciences. – 2010. – v.42, №8.– pp.42 47. Циганок В.В., Андрійчук О.В. Врахування компетентності експертів при визначенні групового ранжирування. Реєстрація, зберігання і обробка даних. – 2011. – т.13. – №1.– с.94-105. Циганок В.В. Агрегація групових експертних оцінок, отриманих у різних шкалах / В.В.Циганок // Реєстрація, зберігання і обробка даних. – 2011. – т.13. – №4.– (у друці) Tsyganok V.V. Providing sufficient strict individual rankings’ consistency level while group decision-making with feedback. Journal of Modelling in Management, – in print – 2011. Каденко С.В. Метод повышения согласованности индивидуальных экспертных ранжирований при их агрегации // С.В.Каденко, В.В.Цыганок / Проблемы управления и информатики. – 2012. – (в печати) Tsyganok V.V. Significance of Expert Competence Consideration while Group Decision-Making using AHP // V.V.Tsyganok, S.V.Kadenko, O.V.Andriichuk / International Journal of Production Research. – 2012. – in print

Публікації Каденко С. В. Удосконалення методу визначення коефіцієнтів відносної вагомості критеріїв на основі ординальних оцінок / С. В. Каденко // Реєстрація зберігання і обробка даних – 2008 - Том 10, № 1 – с. 137-149. Тоценко В. Г. Об одном подходе к рейтингованию высших учебных заведений / В. Г. Тоценко, С. В. Каденко, Т. Г. Сигал // Проблемы управления и информатики – № 1 – 2008 – С. 87-95. Циганок В.В. Дослідження феномену реверсу рангів при застосуванні методів парних порівнянь. Реєстрація, зберігання і обробка даних. – 2008. – т.10, №3.– с.96-101.. Tsyganok V.V. Investigation of the aggregation effectiveness of expert estimates obtained by the pairwise comparison method. Mathematical and Computer Modelling. – August 2010. – v.52, №3-4. – pp.538-544. Цыганок В.В. Имитационное моделирование экспертных оценок для тестирования методов обработки информации в системах поддержки принятия решений // В.В.Цыганок, С.В.Каденко, О.В.Андрейчук / Проблемы управления и информатики. – 2011. – №6. – с.84-94. Циганок В.В. Концепція створення систем підтримки прийняття рішень, що адаптивні до рівня компетентності експертів. Реєстрація, зберігання і обробка даних. – 2011. – т.13. – №2.– с.106-114. Циганок В.В. Вибір шкали оцінювання експертом у процесі виконання ним парних порівнянь в системах підтримки прийняття рішень / В.В.Циганок // Реєстрація, зберігання і обробка даних. – 2011. – т.13. – №3.– с.92-105. Tsyganok V.V., Kadenko S.V., Andriychuk O.V. Significance of Expert Competence Consideration while Group Decision Making using AHP. // Proceedings of the 11th International Symposium on the Analytic Hierarchy/Network Process. Sorrento, Naples, Italy. June 15 – 18, 2011 / ISSN 1556-8296 // ISBN 978-88-906147-0-5. – Access mode: http://204.202.238.22/isahp2011/dati/pdf/154_078_Tsyganok.pdf Tsyganok Vitaliy, Kadenko Sergey “SOLON” DSS Family and their Implementation for Project Selection in Weakly Structured Domains // Proceedings of the 11th International Symposium on the Analytic Hierarchy/Network Process. Sorrento, Naples, Italy. June 15 – 18, 2011 / ISSN 1556-8296 Kadenko S.V. Deriving Criterion Weights From Expert Judgements: Simple and Fuzzy Rankings vs Saaty’s Prefernce Scale // Proceedings of the 11th International Symposium on the Analytic Hierarchy/Network Process. Sorrento, Naples, Italy. June 15 – 18, 2011 / ISSN 1556-8296 // ISBN 978-88-906147-0-5. – Access mode: http://204.202.238.22/isahp2011/dati/pdf/ 82_0142_Kadenko.pdf Каденко С.В. Обчислення відносних ваг критеріїв оцінки альтернатив на основі чітких та нечітких ранжирувань // Системи підтримки прийняття рішень. Теорія і практика // Збірник доповідей науково-практичної конференції з міжнародною участю. – Київ: НАН України, Інститут проблем математичних машин і систем. – 2011. – с.67-70. Tsyganok V.V. Simulation of Expert Judgements for Testing the Methods of Information Processing in Decision-Making Support Systems // V.V.Tsyganok., S.V.Kadenko, O.V.Andriichuk / Journal of Automation and Information Sciences. – 2011. – v.43, issue 12. – p.21 32.

За результатами НДР Опубліковано: 17 статей (із них 3 у друці), 9 тез на конференціях Захищено: 1 кандидатська дисертація Отримано: 2 позитивні рецензії Заступника директора з наукової роботи Навчально-наукового комплексу «Інститут прикладного системного аналізу» при НТУУ „КПІ” НАН України та МОН України д.т.н., професора Н.Д.Панкратової Завідувача відділу Інституту космічних досліджень НАНУ та НКАУ д.т.н., професора Л.І.Самойленко

Дякую за увагу!