Презентація на тему:
Моделі и моделювання

Моделі и моделювання Тема 1. Моделі та їх типи © К.Ю. Поляков, 2007

Моделі в нашому житті

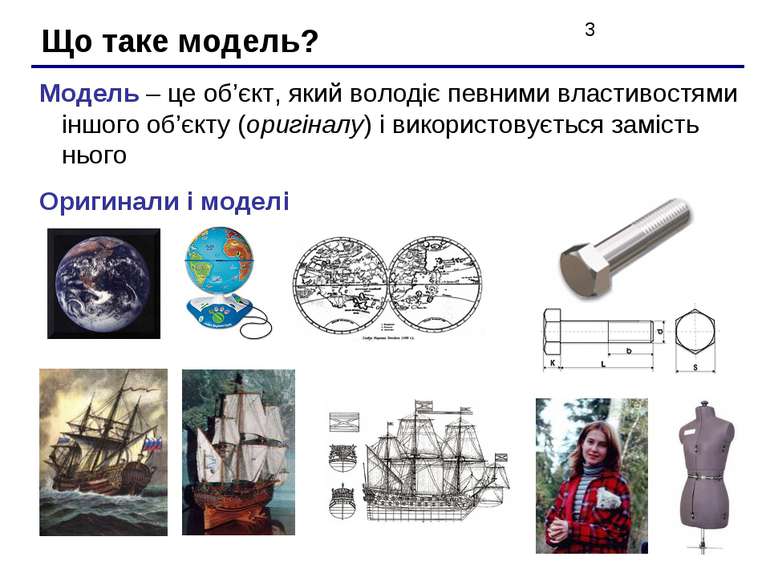
Що таке модель? Модель – це об’єкт, який володіє певними властивостями іншого об’єкту (оригіналу) і використовується замість нього Оригинали і моделі

Що можна моделювати? Моделі об’єктів: Зменшені копії будівель, кораблів, літаків … моделі ядра атома, кристалічних решіток креслення … Моделі процесів: зміна екологічної ситуації економічні моделі історичні моделі … Моделі явищ: землетрус Сонячне затемнення цунамі …

Моделювання Моделювання – це створення і використання моделей для вивчення оригіналів. Коли використовують моделювання: оригінал не існує древній Єгипет наслідки ядерної війни дослідження оригіналу небезпечне для життя або дороге: керування ядерним реактором випробування нового скафандра для космонавтів розробка нового літака чи корабля оригінал складно досліджувати безпосередньо: Сонячна система, Галактика (великі розміри) атом, нейтрон (маленькі розміри) процеси в двигуні внутрішнього згорання (дуже швидкі) геологичні явища (дуже повільні) цікавлять лише деякі властивості оригиналу перевірка фарби для фюзеляжу літака

Цілі моделювання дослідження оригіналу вивчення суті об’єкту чи явища аналіз («що буде, якщо …») навчитись прогнозувати наслідки різних впливів на оригінал синтез («як зробити так, щоб …») навчитись керувати оригіналом, впливаючи на нього оптимізация («як зробити краще») вибір кращого рішення у заданих умовах

Природа моделей матеріальні (фізичні, предметні) моделі: інформаційні моделі являють собою інформацію про властивості та стан об’єкту, процесу, явища, і його взаємозв’язки із зовнішнім світом: вербальні – словесні чи мисленнєві знакові – виражені за допомогою формальної мови графічні (рисунки, схеми, карти, …) табличні математичні (формули) логічні (різні варіанти вибору дій на основі аналізу умов) спеціальні (ноти, хімічені формули)

Моделі за областю застовування навчальні (в т.ч. тренажери) дослідні – при створенні нових технічних засобів науково-технічні аеродинамічна труба дослідження в басейні Імітатор сонячного випромінювання Вакуумна камера в Інституті космічних досліджень вібростенд НПО «Енергія»

Спеціальні види моделей ігрові – враховують дії супротивника моделі економічних ситуацій моделі військових дій спортивні ігри тренінги персоналу імітаційні не можна заздалегідь визначити чи передбачити поведінку системи; можна імітувати її реакцію на зовнішні впливи; максимальне врахування всіх факторів; лише чисельні результати; вибір кращого рішення методом проб і помилок в ході багатократних експериментів Приклади: випробування ліків на мишах, мавпах, … математичне моделювання біологічних систем моделі бізнесу і управління моделі процесу навчання

Моделі за характером зв’язків детерміновані зв’язки між вхідними та вихідними величинами чітко задані при однакових вхідних даних щоразу отримуємо однакові результати Приклади рух тіла, що кинули під кутом до горизонту розрахунки за відомими формулами модель штатної роботи механізму ймовірнісні (стохастичні) враховують ймовірність подій в реальному світі при однакових вхідних даних щоразу отримуємо дещо різні результати Приклади рух тіла з врахуванням сили вітру броунівский рух частинок вплив хвиль на корабель моделювання дій людини

Моделі за фактором часу статичні – описують оригінал в заданий момент часу сили, що діють на тіло у стані спокою результати огляду лікаря фотографія динамічні модель руху тіла явища природи (блискавка, землетрус, цунамі) історія хвороби відеозапис події

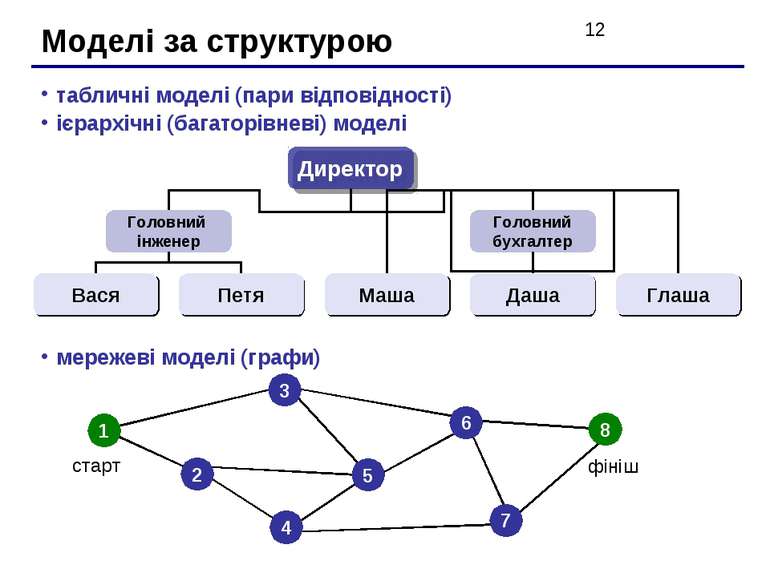
Моделі за структурою табличні моделі (пари відповідності) ієрархічні (багаторівневі) моделі мережеві моделі (графи)

Моделі та моделювання Тема 2. Етапи моделювання © К.Ю. Поляков, 2007

I. Постановка задачі дослідження оригіналу Вивчення суті обєкту чи явища аналіз («що буде, якщо …») навчитися прогнозувати наслідки різних впливів на оригінал синтез («як зробити, щоб …») навчитися керувати оригіналом, здійснюючи на нього вплив оптимізація («як зробити краще») вибір найкращого рішення у заданих умовах

I. Постановка задачі Добре поставлена задача: описані всі звязки між початковими даними та результатом Відомі всі початкові дані Рішення існує Рішення єдине Погано поставлена задача: Вінні Пух и Пятачок побудували капкан для слонопотама. Чи вдасться його зловити? Малюк і Карлсон вирішили поділити два горішки – маленький і великий. Як це зробити? Знайти максимальне значення функції y = x2 (немає рішення). Знайти функції, графік яких проходить через точки (0,1) і (1,0) (не єдине рішення).

II. Розробка моделі Вибрати тип моделі Визначити важливі властивості оригіналу, які потрібно включити в модель, і які відкинути як несуттєві (для даної задачі) Побудудувати формальну модель записану на формальній мові, і яка відображає лише суттєві властивості оригіналу Розробити алгоритм роботи моделі алгоритм - це чітко певний порядок дій, які потрібно виконати для вирішення завдання

III. Тестування моделі Тестування - це перевірка моделі на простих початкових даних з відомим результатом. Приклади: пристрій для додавання багатозначних чисел - перевірка на однозначних числах модель руху корабля - якщо кермо стоїть рівно, курс не повинен мінятися модель накопичення грошей в банку - при ставці 0% сума не повинна змінюватися

IV. Експеримент Експеримент - це дослідження моделі в умовах, що нас цікавлять. Приклади: пристрій для додавання чисел - робота з багатозначними числами модель руху корабля - дослідження в умовах морського шторму модель накопичення грошей в банку - розрахунки при ненульовій ставці

V. Аналіз результатів Можливі висновки: завдання вирішене необхідно змінити алгоритм або умови моделювання необхідно змінити модель (наприклад, врахувати додаткові властивості) необхідно змінити постановку завдання

Приклад. Завдання. Мавпа хоче збити банани на пальмі. Як їй треба кинути кокос, щоб поцілити в банани? Аналіз завдання: чи всі початкові дані відомі? чи є рішення? чи єдине рішення?

I. Постановка задачі Початкова інформація: кокос і банан вважаємо матеріальними точками відстань до пальми відома зріст мавпи відомий висота, на якій висить банан, відома мавпа кидає банан з відомою початковою швидкістю опір повітря не враховуємо За цих умов потрібно знайти початковий кут, під яким треба кинути горіх.

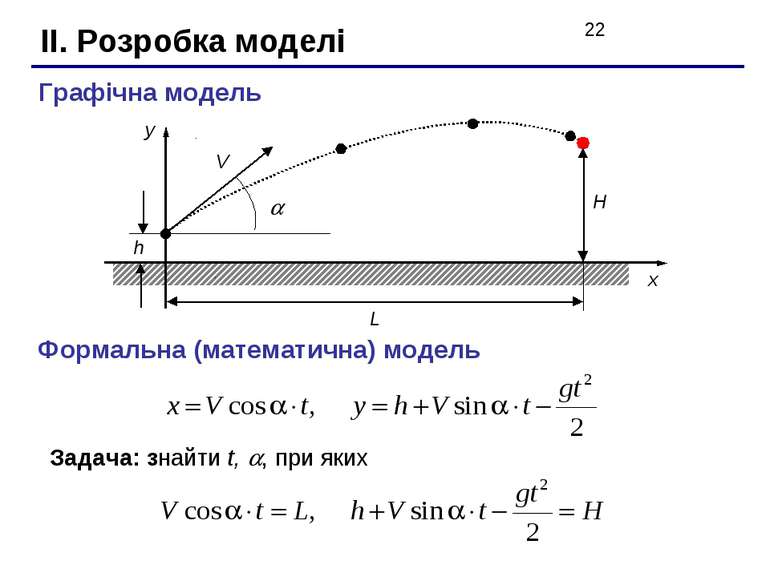
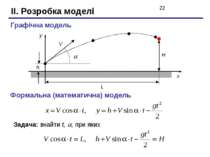
II. Розробка моделі Графічна модель h Формальна (математична) модель Задача: знайти t, , при яких

III. Тестування моделі при нульовій швидкості кокос падає вертикально вниз при t=0 координати рівні (0,h) при кидку вертикально вгору (a=90o) координата x не міняється при деякому t координата у починає зменшуватися (гілки параболи йдуть вниз) Математична модель

IV. Експеримент Метод I. Міняємо кут . Для вибраного кута будуємо траєкторію польоту горіха. Якщо вона проходить вище за банан, зменшуємо кут, якщо нижче - збільшуємо. Метод II. З першої рівності виражаємо час польоту: Міняємо кут . Для вибраного кута рахуємо t, а потім - значення у при цьому t. Якщо воно більше за H, зменшуємо кут, якщо менше - збільшуємо. не потрібно будувати траекторію для кожного

V. Аналіз результатів Чи завжди мавпа може збити банан? Що зміниться, якщо мавпа може кидати кокос з різною силою (з різною початковою швидкістю)? Що зміниться, якщо кокос і банани не вважати матеріальними точками? Що зміниться, якщо потрібно врахувати опір повітря? Що зміниться, якщо дерево гойдається?