Презентація на тему:
урок математики 6 клас

Дільники натурального числа

Задача Скільком учням порівну можна роздати 12; 10; 9; 5 яблук? Розв'язання: 12 яблук між 1,2,3,4,6,12 учнями; 10 яблук 1,2,5,10; 9 яблук 1,3,9; 5 яблук 1,5? Чому? Оскільки 12 ділиться на 1,2,3,4,6,12; 10 – на 1,2,5,10; 9 - на 1,3,9; 5 - на 1,5. Отже , числа 1,2,3,4,6,12 є дільниками числа 12; числа 1,3,9 є дільниками числа 9.

Знайдіть усі дільники числа 42 Записуємо дільники парами: 1 і 42; 2 і 21; 3 і 14; 6 і 7. Міркуючи таким чином, ми не можемо пропустити жодного дільника числа. Отже, число 42 має дільники 1, 2, 3, 6, 7, 14, 21, 42.

Перевір себе 110; 24; 48; 72; 96. 2; 4; 1; 8 ;16; 32; так так ні

Досконалі числа Число, яке дорівнює сумі своїх дільників, не враховуючи самого числа, називається досконалим числом. Наприклад : 6 = 1+2+3; 28 =1+2+4+7+14; 496=1+2+4+8+16+31+62+124+248. Всього їх знайдено 24

Ознаки подільності на 2,5 і 10

Якщо запис натурального числа закінчується на 0, то це число ділиться без остачі на 10.  Якщо запис натурального числа закінчується будь-якою іншою цифрою, то воно не ділиться без остачі на 10.  Приклади:  680 ділиться на 10; 104 не ділиться на 10. 

Якщо запис натурального числа закінчується цифрами 0 або 5, то це число ділиться без остачі на 5.  Якщо запис числа закінчується будь-якою іншою цифрою, то число не ділиться на 5 без остачі. Приклади:  370 і 1485 діляться без остачі на 5; числа 537 і 4008 без остачі на 5 не діляться. 

Як довідатись мені: Ділиться число на 2, чи ні? Щоб не помилитися, На останню цифру треба подивитися. Число на 2 поділиться в нас гарно, Якщо ця цифра.. парна

Цифри 0, 2, 4, 6, 8 називають парними, а цифри 1, 3, 5, 7, 9 - непарними.  Натуральні числа називають парними, якщо вони закінчуються парною цифрою, і непарними, якщо вони закінчуються непарною цифрою. Якщо запис натурального числа закінчується парною цифрою, то це число ділиться без остачі на 2, а якщо непарною цифрою - то число не ділиться без остачі на 2.  Приклади:  8, 60, 574 - діляться на 2; 13, 25, 1001 - не діляться на 2. 

Із чисел 125,460,195,224,876,1540,7400,3048,5605,1380 випиши ті, які діляться: а) на 2 : б) на 5: в) на 10: 460; 224; 876;1540; 7400; 3048;1380; 125; 460; 195; 1540; 7400; 5605;1380; 460; 140;7400;1380.

Це корисно знати Натуральне число ділиться на 4, якщо дві його останні цифри утворюють число, яке ділиться на 4 або останні цифри нулі.  Приклади:  78 536 ділиться на 4, оскільки 36 ділиться на 4; 8422 не ділиться на 4, оскільки 22 не ділиться на 4.  Натуральне число ділиться на 25, якщо число, утворене двома його останніми цифрами ділиться, на 25 або останні цифри нулі.  Приклади:  57 375 ділиться на 25, оскільки 75 ділиться на 25; 8035 не ділиться на 25, оскільки 35 не ділиться на 25. 

Розв'яжіть задачу: Фермер купив 25 корів. Чи можна стверджувати, що його покупка коштуватиме 874900 грн. 156375 грн. 100005 грн. 125330 грн. 948225 грн. (вартість кожної корови виражаеться натуральным числом). так так так ні ні

Ознаки подільності на 9 і на 3

Як довідатись мені - Ділиться число на 3, чи ні? Зробимо так я і ти : Суму цифр у числі треба знайти. Якщо сума поділиться на 3, То й число поділиться на 3

Якщо сума цифр числа ділиться на 3, то й саме число ділиться на 3. Якщо сума цифр числа не ділиться на 3, то й число не ділиться на 3.  Приклади: 276 ділиться на 3, оскільки 2 + 7 + 6 = 15, а 15 ділиться на 3; 563 не ділиться на 3, оскільки 5 + 6 + 3 = 14, а 14 не ділиться на 3.

Якщо сума цифр числа ділиться на 9, то й саме число ділиться на 9. Якщосума цифр числа не ділиться на 9, то й число не ділиться на 9.  Приклади:  5787 ділиться на 9, оскільки 5 + 7 + 8 + 7 = 27, а 27 ділиться на 9; 359 не ділиться на 9, оскільки 3 + 5 + 9 = 17, а 17 не ділиться на 9. 

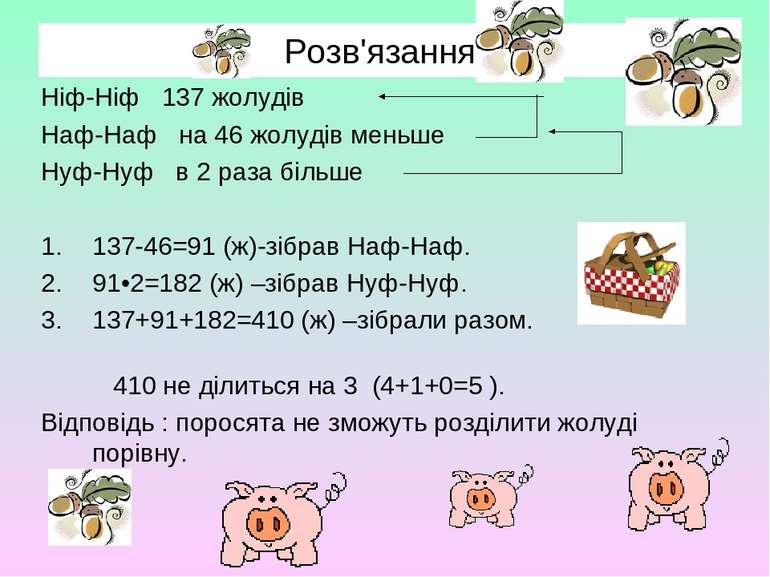
Розв'яжіть задачу. Три поросята Ніф-Ніф, Наф-Наф и Нуф-Нуф зібрали в лісі жолуді. Ніф-Ніф зібрав 137 жолудів, Наф-Наф зібрав на 46 жолудів меньше, а Нуф-Нуф – в 2 раза більше, ніж Наф-Наф. Чи зможуть поросята розділити жолуді порівну?

Розв'язання. Ніф-Ніф 137 жолудів Наф-Наф на 46 жолудів меньше Нуф-Нуф в 2 раза більше 137-46=91 (ж)-зібрав Наф-Наф. 91•2=182 (ж) –зібрав Нуф-Нуф. 137+91+182=410 (ж) –зібрали разом. 410 не ділиться на 3 (4+1+0=5 ). Відповідь : поросята не зможуть розділити жолуді порівну.

Які цифри можна підставити замість зірочки, щоб число без остачі Ділилось на 9 286* 5*1 75*11 Ділилось на 3 5*76 900* 4*2 2 4 3 0,3,6,9 0,3,6,9 0,3,6,9

Із цифр 0, 3, 4, 5 складіть : а) трицифрові числа, які діляться на 2 і 5 одночасно; 340, 430, 350, 530, 540, 450. б) двоцифрові числа, які діляться 3; 30, 45, 54. в) двоцифрові непарні числа; 43, 45, 53. г) числа, які діляться на 9. 45, 54, 450, 540, 504, 405.

Це корисно знати Натуральне число ділиться на 6, якщо воно одночасно ділиться на 2 і на 3. Приклади: 762 ділиться на 6, оскільки 762 ділиться і на 2,і на 3; 754 не ділиться на 6, оскільки 754 не ділиться на 3. Натуральне число ділиться на 8, якщо три його останні цифри утворюють число, яке ділиться на 8. Приклади: 15160 ділиться на 8, оскільки 160 ділиться на 8; 5063 не ділиться на 8, оскільки 63 не ділиться на 8.

Натуральне число називають простим, якщо воно має два різні дільники:одиницю і саме це число.  Число 17 має два дільники, значить, воно просте. Натуральне число називають складеним, якщо воно має більше двох дільників.  Число 9 має три дільники (1, 3 і 9), значить, воно є складене.

Запам'ятай,це може пригодиться, Що не просте і не складне число – це… одиниця

1 2 3 4 5 6 7 8 9 10 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 Решето Ератосфена Решето Ератосфе на в математиці — простий стародавній алгоритм знаходження всіх простих чисел менших деякого цілого числа n, що був створений давньогрецьким математиком Ератосфеном.

(простим) Якщо число два дільники лиш має, То зараз кожен з вас згадає, Що це число і я , і ти – Усі назвем його …

Напишіть всі прості числа, при яких правильна нерівність 23≤ Х≤49 23 29 31 37 41 43 47

Доведіть,що числа є складеними 22 519 225 701 541 169 2211

Розкладання натуральних чисел на прості множники

108 2 420 10=2∙5 54 2 42 2 27 3 21 3 9 3 7 7 3 3 1 1 При будь-якому способі запису одержуємо один і той самий розклад, якщо не враховувати порядку розміщення множників.  Приклади:  180 = 2•2•3•3•5;  1368 = 2•2•2•3•3•19. Розкласти складене число на прості множники означає записати дане число у вигляді добутку простих чисел . 

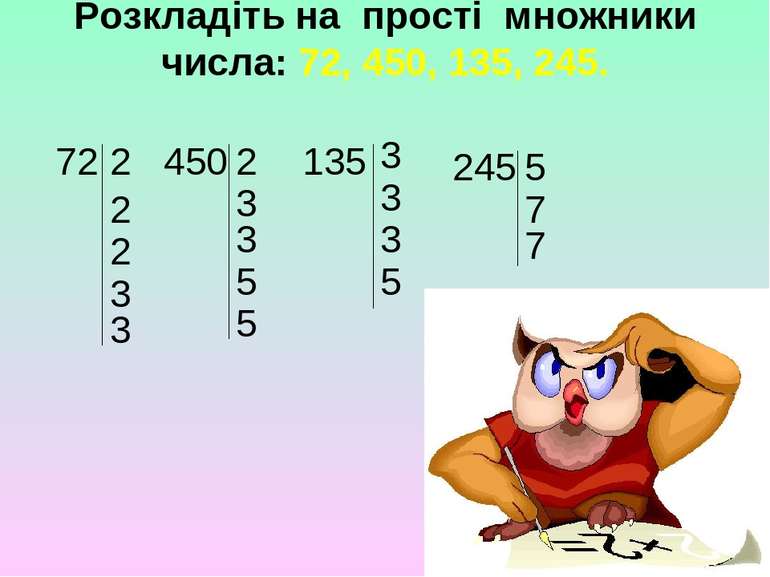
Розкладіть на прості множники числа: 72, 450, 135, 245. 72 2 2 2 3 3 2 3 3 5 5 450 3 3 3 5 135 5 7 7 245

Знайдіть усі дільники чисел 98,216,2272 Дільники числа 98: 1; 2; 7; 14; 49; 98. Дільники числа 140: 1; 2; 4; 5; 7; 10; 14; 20; 28; 140. Дільники числа 216: 1; 2; 3; 4; 6; 9; 8; 27; 24; 36; 54; 72;108; 216.

Найбільший спільний дільник (НСД)

Задача. Учні 6 класу до Нового року одержали однакові подарунки. Скільки учнів у класі, якщо було куплено 87 апельсинів і 58 шоколадних плиток? Розв'язання: Як бачимо, для розв'язання цієї задачі нам потрібно знайти спільний дільник двох даних чисел, т. б. число, на яке діляться обидва числа. 87 3 58 2 29 29 29 1 1 НСД(87,58)=29 Відповідь: у класі було 29 учнів

Для знаходження НСД двох чисел можна розкласти ці числа на прості множники і знайти добуток їх спільних множників.  Приклади: а) Знайти НСД (6600; 6300): 6600 = 2 • 2 • 2 • 3 • 5 • 5 • 11, 6300 =2 • 2 • 3 • 3 • 5 • 5 • 7, НСД (6600; 6300) = 2 • 2 • 3 • 5 • 5 = 300;  б) Знайти НСД (34 398; 1260; 6552): 34 398 = 2 • 3 • 3 • 3 • 7 • 7 • 13, 1260 = 2 • 2 • 3 • 3 • 5 • 7, 6552 = 2•2•2•3•3•7•13, НСД (34 398; 1260; 6552) = 2 • 3 • 3 • 7 = 126. 

Запам'ятай Якщо НСД(a,b)=1, то a і b взаємно прості числа. Приклади:  75 і 14 - взаємно прості числа, оскільки НСД (75; 14) = 1; 20, 9 і 77 взаємно прості числа, оскільки НСД (20; 9; 77) = 1.

Всі ми знаєм як паління шкодить здоров'ю, знайдіть НСД(540;735) і тоді ми дізнаємося на скільки хвилин 1 цигарка скорочує життя людини. НСД (540;735)= 15

Задача. Троє поросят: Ніф –Ніф, Нуф-Нуф і Наф-Наф , закінчивши будівництво своїх будинків, вирішили влаштувати свято. Для подарунків своїм гостям вони приготували 360 цукерок і 420 горіхів. Яку найбільшу кількість гостей змогли б запросити поросята, якщо цукерки і горіхи планували розподіляти порівну? Скільки цукерок і горішків отримав кожен гість?

Розв'язання Кожне з чисел 360 і 420 повинно ділитися на кількість запрошених гостей. Знайдемо НСД(360,420)= Отже, можна запросити 60 гостей. У кожному подарунку буде 6 цукерок (360:60=6) і 7 горішків (420:60=7) 60

Задача - жарт Шість розбійників пограбували царя, вони вкрали менше сотні однакових золотих злитків. Почали вони ділити злитки порівну, але один залишився. Розбійники побилися, і одного з них було вбито. Вони знов почали ділити злитки, і знов один залишився. Далі вони побилися, одного розбійника було вбито. Це продовжувалося доти, доки не залишився один розбійник, який утік з цього місця. Скільки було злитків золота?

Розв'язання Треба знайти число, яке менше 100 і при діленні на 2,3,4,5,6 дає остачу 1, тому, воно більше на 1 за те число, яке ділиться без остачі на 2,3,4,5,6. а це число 60. Відповідь: 61 злиток.

Найменше спільне кратне (НСК)

Кратні натурального числа Кратним натуральному числу а називають натуральне число, яке ділиться на а без остачі.  Приклади: для числа 18 кратними є числа: 18, 36, 54, 72, 90, 108, 126 і т.д.; для числа 7 кратними є числа: 7, 14, 21, 28, 35, 42, 49 і т.д.  Отже, треба запам'ятати: 1) будь-яке число має нескінченну кількість кратних; 2) найменшим кратним для числа є саме це число. 

Найменшим спільним кратним натуральних чисел а і b називають найменше натуральне число, яке кратне і а, і b.  Треба запам'ятати: 1) якщо одне із двох натуральних чисел ділиться на друге число, то більше з цих двох чисел є їх найменшим спільним кратним; 2) якщо два числа є взаємно простими, то найменше спільне кратне цих чисел дорівнює їх добутку.  Приклади:  НСК (9; 18) = 18; НСК (2; 8; 16) = 16, оскільки 8 ділиться на 2, а 16 ділиться на 8; НСК (7; 10) = 70, оскільки 7 і 10 - взаємно прості числа. 

Щоб знайти найменше спільне кратне декількох натуральних чисел, треба: 1)розкласти їх на прості множники; 2) виписати множники, що входять у розклад (краще найдовший) одного з чисел; 3) дописати до них ті множники, що є в розкладі інших чисел; 4) знайти значення утвореного добутку. 

Знайдіть найменше спільне кратне чисел 34,51,68 Розв'язання 34 2 17 17 1 51 3 17 17 1 68 2 34 2 17 17 1 НСК(34,51,68)= 2 ∙ 2 ∙ 17 ∙ 3 Відповідь: 204 = 204

Перевірте себе НСК (20;70;15) = НСК (18;45)= НСК (30;40) = НСК (210;350) = 120 90 420 1050

В понеділок Чебурашка, Карлсон і Вінні-Пух одночасно відправилися в довготривалу подорож по казковій країні. Казкові герої надсилають про себе повідомлення: Чебурашка через кожні 6 днів, Карлсон – 12 днів, Вінні-Пух - 9 днів. Через скільки днів і в який день неділі одночасно прийдуть звістки від всіх трьох казкових героїв? Задача

Розв'язання Кількість днів, коли прийде звістка від трьох друзів одночасно, повинна ділитися без остачі і на 6, і на 12, і на 9, тобто має бути кратною 6,12,9. Знайдемо НСК(6,9,12)= Відповідь: звістка від казкових героїв прийде через 36 днів і це буде в 36. четвер.