Презентація на тему:
Світ многокутників

Світ многокутників

Многокутники однорідні   опуклі однорідні   неопуклі Тіло Архімеда Тіло Платона опуклі призми і антипризми Тіла Кеплера- Пуансо неопуклі напівправильні однорідні багатогранники не опуклі призми і антипризми

Правильними многогранниками називають опуклі багатогранники, всі грані і всі кути яких рівні, причому грані - правильні багатокутники.        У кожній вершині правильного багатогранника сходиться одне і те ж число ребер.     Всі двогранні кути при ребрах і всі багатогранні кути при вершинах правильного багатокутника рівні.     Правильні багатогранники - тривимірний аналог плоских правильних багатокутників.

Правильні многокутники Скільки ж їх існує? Розглянемо розгортку вершини багатогранника . Кожна вершина може належати трьом і більше гранях. Спочатку розглянемо випадок , коли межі багатогранника - рівносторонні трикутники . Оскільки внутрішній кут рівностороннього трикутника дорівнює 60 ° , три таких кута дадуть у розгортці 180 °. Якщо тепер склеїти розгортку в багатогранний кут , вийде тетраедр - багатогранник , в кожній вершині якого зустрічаються три правильні трикутні грані. Якщо додати до розгортці вершини ще один трикутник , в сумі вийде 240 °. Це розгортка вершини октаедра. Додавання п'ятого трикутника дасть кут 300 ° - ми отримуємо розгортку вершини ікосаедра . Якщо ж додати ще один , шостий трикутник , сума кутів стане рівною 360 ° - ця розгортка , очевидно , не може відповідати жодному опуклому багатограннику .

Тепер перейдемо до квадратних гранях. Розгортка з трьох квадратних граней має кут 3x90 ° = 270 ° - виходить вершина куба , який також називають Гексаедр . Додавання ще одного квадрата збільшить кут до 360 ° - цієї розгортці вже не відповідає ніякої опуклий багатогранник . Три п'ятикутні грані дають кут розгортки 3 * 108 ° = 324 - вершина додекаедра . Якщо додати ще один п'ятикутник , отримаємо більше 360 ° - тому зупиняємося . Для шестикутників вже три грані дають кут розгортки 3 * 120 ° = 360 ° , тому правильного опуклого багатогранника з шестикутними гранями не існує. Якщо ж грань має ще більше кутів , то розгортка матиме ще більший кут . Значить , правильних опуклих багатогранників з гранями , що мають шість і більше кутів , не існує.

Зробимо висновок: Ми переконалися, що існує лише п'ять опуклих правильних багатогранників - тетраедр, октаедр і ікосаедр з трикутними гранями, куб (гексаедр) з квадратними гранями і додекаедр з п'ятикутними гранями. Ці тіла ще називають   тілами Платона.

вогонь тетраєдр ікосаедр   октаєдр   гексаєдр Всесвіт додекаєдр вода земля повітря Починаючи з 7 століття до нашої ери у Стародавній Греції створюються філософські школи, в яких відбувається поступовий перехід від практичної до філософської геометрії. Велике значення в цих школах набувають міркування, за допомогою яких вдалося отримувати нові геометричні властивості. Однією з перших і найвідоміших шкіл була Пифагорейская, названа на честь свого засновника Піфагора. Відмітною знаком піфагорійців була пентаграма, мовою математики-це правильний неопуклий або зірчастий п'ятикутник. Пентаграмме присвоювалося здатність захищати людину від злих духів. Існування тільки п'яти правильних багатогранників відносили до будови матерії і Всесвіту. Піфагорійці, а потім Платон вважали, що матерія складається з чотирьох основних елементів: вогню, землі, повітря та води. Згідно з їх думку, атоми основних елементів повинні мати форму різних Платонових тіл.

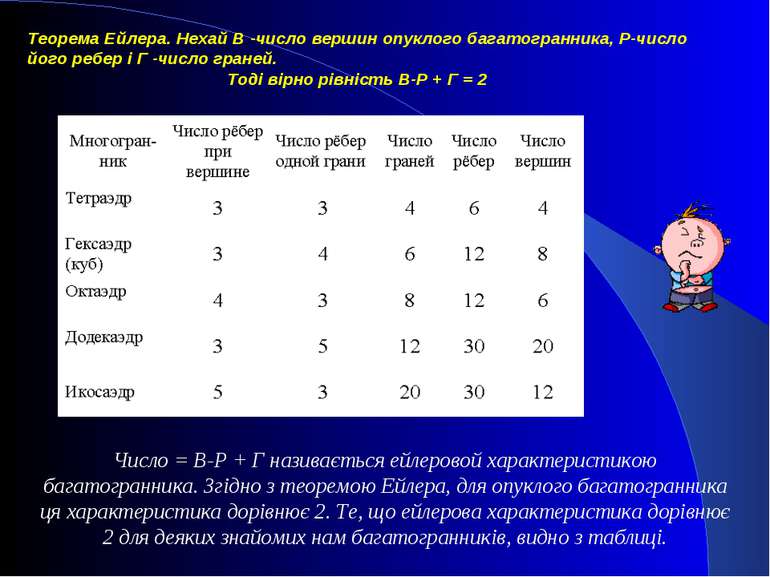
Число = В-Р + Г називається ейлеровой характеристикою багатогранника. Згідно з теоремою Ейлера, для опуклого багатогранника ця характеристика дорівнює 2. Те, що ейлерова характеристика дорівнює 2 для деяких знайомих нам багатогранників, видно з таблиці.

Теорема Эйлера В – Р + Г = 2

Тетраєдр Ікосаєдр Гексаєдр Додекаєдр Октаєдр

Тіла Архімеда Архімедови тілами називаються напівправильні однорідні опуклі багатогранники, тобто опуклі багатогранники, всі багатогранні кути яких рівні, а грані - правильні багатокутники декількох типів.

Тіла Архімеда Тіло Ашкінузе

Тіла Кеплера - Пуансо Серед неопуклих однорідних багатогранників існують аналоги Платонових тіл - чотири правильні неопуклих однорідних багатогранника або тіла Кеплера - Пуансо. Як випливає з їхньої назви, тіла Кеплера-Пуансо - це неопуклі однорідні багатогранники, всі грані яких - однакові правильні багатокутники, і всі багатогранні кути яких рівні. Грані при цьому можуть бути як опуклими, так і неопуклого.

великий зірчастий додекаедр великий ікосаедр малий зірчастий додекаедр

Магнус Веннинджер (1919г.р.)

Багатогранники в мистецтві В епоху Відродження великий інтерес до форм правильних багатогранників проявили скульптори. архітектори, художники. Леонардо да Вінчі (1452 -1519) наприклад, захоплювався теорією багатогранників і часто зображував їх на своїх полотнах. Він проілюстрував правильними і напівправильними многогранниками книгу Ченця Луки Пачолі'' Про божественної пропорції.'' Знаменитий художник, що захоплювався геометрією Альбрехт Дюрер (1471 - 1528), в відомій гравюрі'' Меланхолія'' на передньому плані зобразив додекаедр. художник Ешер

Наука геометрія виникла з практичних завдань , її пропозиції висловлюють реальні факти і знаходять численні застосування . В кінцевому рахунку в основі всієї техніки так чи інакше лежить геометрія , тому що вона з'являється всюди, де потрібна хоча б найменша точність у визначенні форми і розмірів. І техніку, і інженеру , і кваліфікованому робітникові і людям мистецтва геометричне уяву необхідно , як геометру або архітекторові. Математика , зокрема геометрія , являє собою могутній інструмент пізнання природи , створення техніки і перетворення світу . Різні геометричні форми знаходять своє відображення практично у в усіх галузях знань: архітектура , мистецтво. Багатогранники в архітектурі

Велика піраміда була побудована як гробниця Хуфу, відомого грекам як Хеопс. Він був одним з фараонів, або царів давнього Єгипту, а його гробниця була завершена в 2580 до н.е. Пізніше в Гізі було збудовано ще дві піраміди, для сина і онука Хуфу, а також менші за розмірами піраміди для їх цариць. Піраміда Хуфу, сама далека на малюнку, є найбільшою. Піраміда його сина знаходиться в середині і виглядає вище, тому що стоїть на більш високому місці.  Царські гробниці

ТРИ БАШНІ Фаросский маяк складався з трьох мармурових башт, які стояли на підставі з   масивних кам'яних блоків. Перша башта була прямокутна, в ній були кімнати, в яких жили робітники і солдати. Над цією вежею розташовувалася менша, восьмикутна вежа зі спіральним пандусом, провідним у верхню вежу.

Александрівський маяк.

Дякую за увагу :)