Презентація на тему:
"Призма"

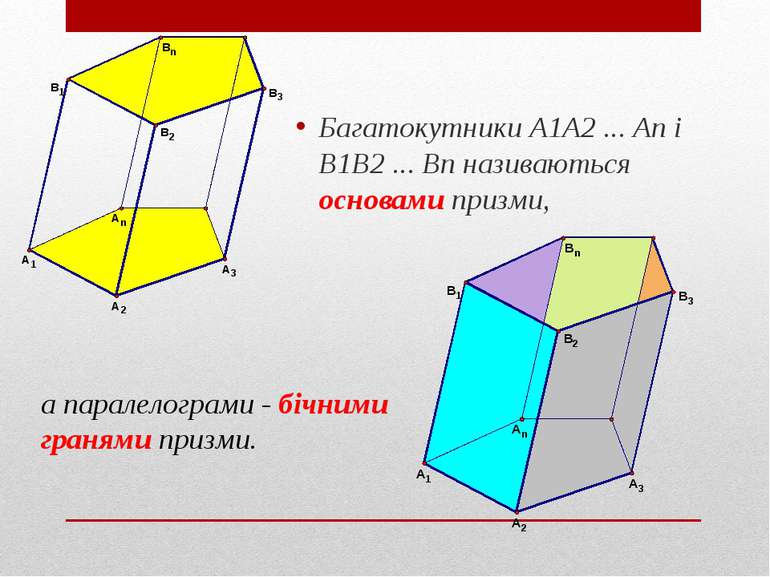
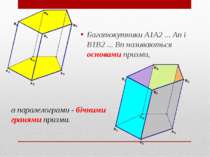
Призма Багатогранник, складений із двох рівних багатокутників A1A2 ... An і B1B2 ... Bn, розташованих в паралельних площинах, і n паралелограмів, називається призмою

V = So* h де V - об'єм призми, So - площа основи призми, h - висота призми. Sповн = Sбіч + 2∙Sосн Sповн – площа повної поверхні; Sбіч – площа бічної поверхні;   Sосн – площа основи призми Довільна призма Площа бічної поверхні довільної призми S = P * l, де P - периметр перпендикулярного перетину, l - довжина бічного ребра. Пряма призма Площа бічної поверхні прямої призми S = P * h, де P - периметр основи призми, h - висота призми.

Багатокутники A1A2 ... An і B1B2 ... Bn називаються основами призми, а паралелограми - бічними гранями призми.

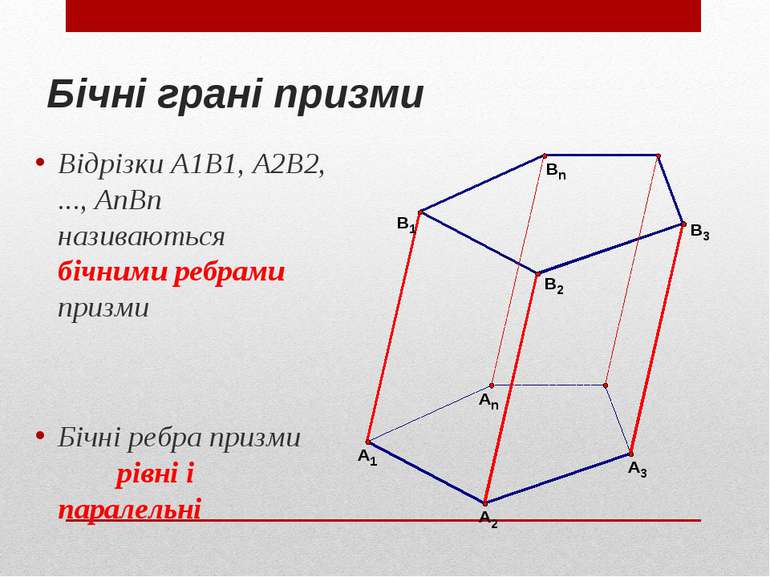
Бічні грані призми Відрізки A1B1, A2B2, ..., AnBn називаються бічними ребрами призми Бічні ребра призми рівні і паралельні

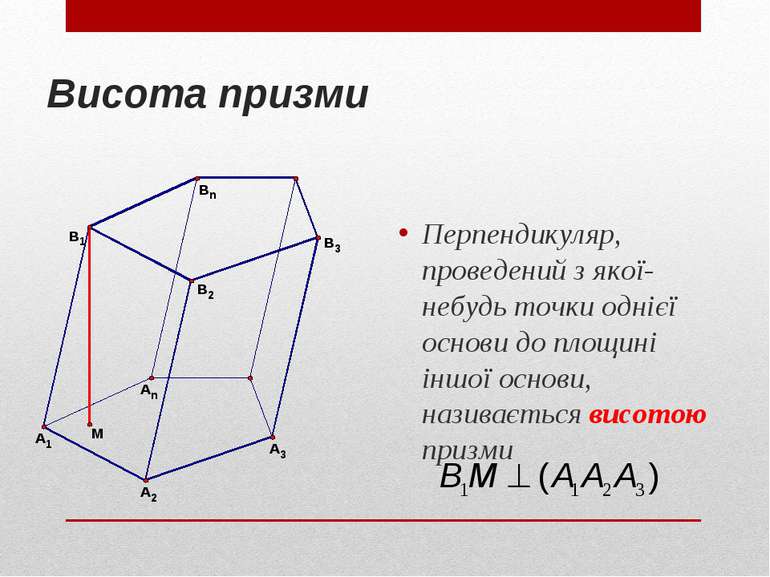
Висота призми Перпендикуляр, проведений з якої-небудь точки однієї основи до площині іншої основи, називається висотою призми

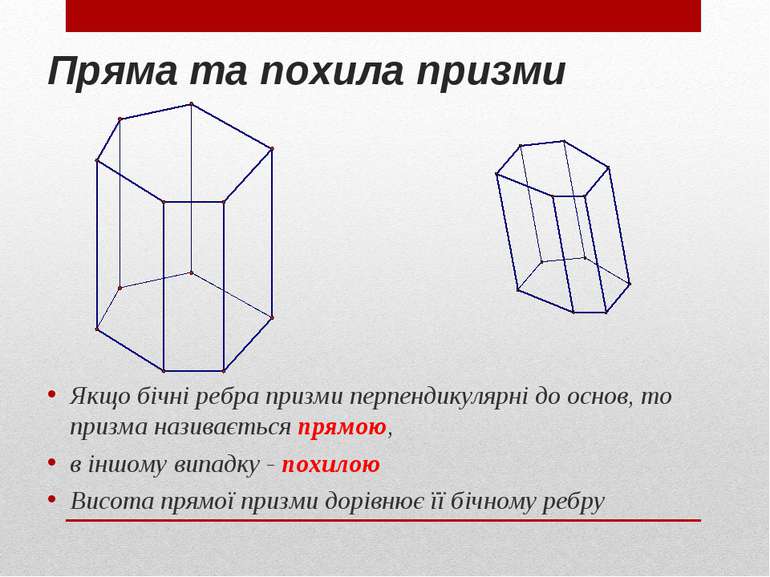
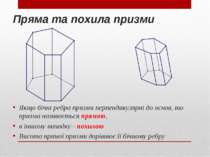
Пряма та похила призми Якщо бічні ребра призми перпендикулярні до основ, то призма називається прямою, в іншому випадку - похилою Висота прямої призми дорівнює її бічному ребру

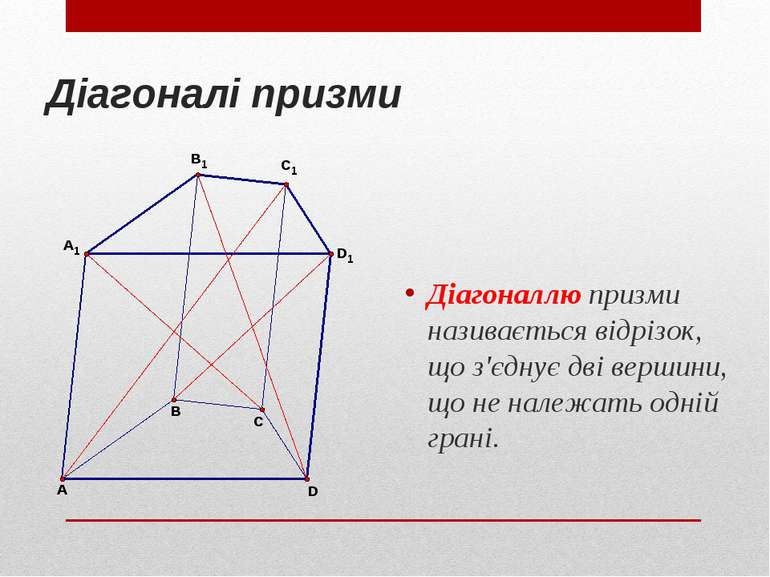
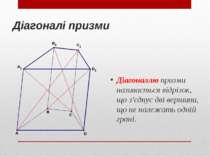
Діагоналі призми Діагоналлю призми називається відрізок, що з'єднує дві вершини, що не належать одній грані.

Навколо правильної трикутної призми описана сфера радіуса 6 см. Радіус сфери, проведений до вершини призми, утворює з бічним ребром кут в 30o. Знайдіть об'єм призми (в см3). Розв'язання Розглянемо призму ABCA1B1C1 Опустимо з центру описаної сфери О перпендикуляри ОN на бічне ребро і OO1 на основу. Точка N буде серединою бокового ребра , а точка O1 - центром описаного кола . За умовою кут OBN дорівнює 30o . Тоді кут OBO1 складе 60o  З трикутника OBN знайдемо BN= см , значить висота призми см. З трикутника OBO1 знайдемо O1B = 3 см. Оскільки в рівносторонньому трикутнику зі стороною а радіус описаного кола дорівнює . то сторона підстави: ; У такому випадку площа підстави складе : Обсяг же піраміди - це добуток площі основи на висоту. (см3) Відповідь : 121,5 см3

V=S*h Довжини усіх ребер правильної трикутної призми дорівнюють між собою. Обчисліть об'єм призми, якщо площа її поверхні дорівнює Де h - a Розв'язання Відповідь:

Презентацію підготував: учень 11 – В класу Левін Владислав Дякую за увагу!