Презентація на тему:
Математичні задачі в художніх творах

Автор проекту: Боровик Карина Керівник проекту: Строкань І.Ф. Математичні задачі в художніх творах

Література і математика - що може об'єднувати ці далекі один від одного області знань? ПРОБЛЕМА Літературу, з її інтересом до духовного світу людини, і математику, яка віддає перевагу строгому науковому підхіду. Літературу ми звикли відносити до гуманітарних наук, а математика вимагає точності і конкретизації фактів. Здавалося б, немає нічого спільного ... Але математика, так само як і поезія, живопис, театр і мистецтво прагне до пізнання і краси. Що люблять, то знаходять скрізь, і було б дивно не зустрітися з математикою в художній літературі.

Математика і література займають дуже значне місце в житті сучасного суспільства, а це означає, викликають до себе величезний інтерес. Актуальність обраної теми продиктована необхідністю зруйнувати стереотип полярності цих наук і довести наявність між ними тісної взаємодії. Достатньо лише побачити за словом число, за сюжетом формулу і переконатися, що література існує не тільки для літераторів, а математика – не тільки для математиків.

Об'єкт дослідження: Предмет дослідження: літературні твори математичні задачі, які можна зустріти в літературних творах

Мета проекту: доведення існування зв'язку між літературою та математикою Завдання: 1) підбір художньої літератури   для дослідження; 2) розв’язання відібраних задач, аналіз отриманих в ході розв’язання результатів; 3) оцінка виконаної роботи та формулювання висновку.

Методи дослідження: пошук, вивчення, аналіз, узагальнення, порівняння.

Старовинні одиниць мір в літературних творах Сажень = 2,134 м - давня східнослов'янська лінійна міра Українська народна казка “Про Опиря”: “Цар вимурував дуже високий стовп у сто сажнів вишини, обкопав його ровом в сто сажнів ширини і сто сажнів глибини” Якими ж були розміри в сучасних мірах: висота стовпа h = 2,134 ×100=213,4(м); ширина і глибина рова a = 2,134 ×100=213,4(м), b = 2,134 ×100=213,4(м). 213,4м 213,4м 213,4м

Корець = 100кг – українська старовинна міра сипких тіл Українська народна казка “Як Гуцул наймався до попа.” Гуцул: “Дасте на рік три корці пшениці… ” Скільки кілограмів пшениці отримав Гуцул у попа за рік ? m = 3 × 100 = 300 (кг)

Дюйм = 2,54 см – англійська одиниця довжини Дж.К.Ролінг “Гаррі Поттер”. Оллівандер про паличку Гаррі Поттера: ”Гостролист і перо фенікса, одинадцять дюймів”. Оллівандер про паличку Беллатриси Лестрейндж: “Грецький горіх і сердечна жила дракона, дванадцять і три чверті дюйму” Оллівандер про паличку Драко Малфоя: “Бояришник і волос єдинорога. Рівно десять дюймів” Порівняймо чия паличка довша у сучасних мірах: 1) 11 × 2,54 = 27,94(см) – паличка Гаррі Поттера 2) 12,75 × 2,54 = 32,385 (см) – паличка Беллатриси Лестрейндж 3) 10 × 2,54=25,4(см) – паличка Драко Малфоя

Математичні задачі в художніх творах М. М. Носов «Федькова задача»: «На млин доставили чотириста п'ятдесят мішків жита, по вісімдесят кілограмів у кожному. Жито змололи, причому, з шести кілограмів зерна вийшло 5 кілограмів борошна. Скільки знадобилося машин для перевезення всього борошна, якщо на кожній машині вміщалося по три тонни борошна? » Розв’язання: 1) 450 × 80=36000(кг) – всього зерна 2) 36000:6=6000(разів) – по 6 кг зерна в 450 мішках 3) 6000 × 5=30000(кг) – муки 1 тонна = 1000 кілограмів 4) 30000:3000 = 10(маш.) – для перевезення муки Висновок: умова цієї задачі сприяє отриманню логічної відповіді

А.П.Чехов” Розмазня” «Я завжди платив гувернантка по тридцяти карбованців в місяць ... Прожили ви два місяці ... Отже, шістдесят карбованців ... Відняти дев'ять неділь ... та три свята ...Чотири дні Микола хворів ... Три дні у вас боліли зуби ... Під Новий рік ви розбили чашку з блюдечком. геть два карбованці... По вашому недогляд Микола порвав сюртучок ... Геть десять Покоївка теж по вашому недогляд вкрала черевики ... Геть ще п'ять... Ви взяли в мене десятькарбованців...і в моєї дружини три карбованці... Залишається одинадцять…» А тепер перевіримо чи правильні були розрахунки 1) 60 – 12=48(к.) – мінус дев'ять неділь і три свята 2) 48 – 7=41(к.) – мінус чотири дні хвороби і три дні хворих зубів 3) 41 – 2=39(к.) – мінус розбиті чашка й блюдце 4) 39 –10 – 5= 24(к.) – мінус порваний сюртук і вкрадені черевички 5) 24 – 10 – 3 =11(к.) – мінус борги Висновок: умова задачі сприяє розвитку навиків точних математичних розрахунків

А.П.Чехов”Репетитор” Арифметична задача, яка так збентежила семикласника Єгора Зіберова «Купець купив 138 аршин чорного і синього сукна за 540 карбованців. Питається, скільки аршин купив він того й іншого, якщо синє сукно коштувало 5 карбованців за аршин, а чорне - 3 карбованців?» Розв’язання. Нехай купили х аршин чорного сукна і (138 - х) аршин синього. Тоді за чорне сукно заплатили 3х рублів, а за синє – 5 (138 - х) рублів. Так як всього заплатили 540 рублів, то складаємо рівняння: 3х + 5(138 – х) = 540 2х = 150 х = 75 Виходить, що купили 75 аршин чорного і 63 аршина синього сукна.

Жюль Верн “П'ятнадцятирічний капітан” Герої роману почали свій шлях з Оклендського порту, що у Новій Зеландії і потрапили у місто Казонде у трьохста милях від річки Кванзи. Я вирішила провести обчислення, яка ж відстань між портом і містом, якщо наші мандрівники спочатку дійшли до річки. Миля=1853,184м=1,853184км – староанглійська одиниця довжини. 1)300 × 1,853184 =555,9552(км)– відстань від річки до міста За допомогою фізичної карти масштабом 1:85000000 (в 1см 850км) і лінійки я знайшла відстань від порту до річки 2) 16,5 × 850=14025(км) – відстань від порту до річки 3) 14025+555,9552=14580,9552(км) - відстань від порту до міста 14580,9552км

Жюль Верн "Таємничий острів". Герої Верна вимірювали висоту скелі. Відстань від кілочка до жердини так відноситься до відстані від кілочка до основи стіни, як висота жердини до висоти стіни. "- якщо ми виміремо дві перші відстані,то, знаючи висоту жердини, зможемо обчислити четвертий, невідомий член пропорції, тобто висоту стіни.» 0бидві горизонтальні відстані були виміряні: менша дорівнювала 15 футам, більша - 500 футам. Після закінчення вимірів інженер склав наступний запис: 15:500 = 10 :х 500 × 10 = 5000 5000: 15 = 333,3 "Значить, висота гранітної стіни дорівнювала 333 футам"

Г.Б.Остер “Зарядка для хвоста” «Зріст удава складає 38 папуг, 5 мавп або 2 слоненяти.» Перевіримо,чи дійсно це так ? За науковими даними: середній зріст папуги 22 см, мавпи 77 см, слоненяти 335 см = 3м 35см, удава 10м. 1000 : 22 ≈ 45,45 або 45 папуг 1000 : 77 ≈ 12,99 або 12 мавп 1000 : 335 ≈ 2,99 або 2 слоненяти Висновок: в житті довжина удава приблизно дорівнює довжині 45 папуг, 12 мавп, 2 слоненят. Автор у своєму творі дещо знехтував точними даними.

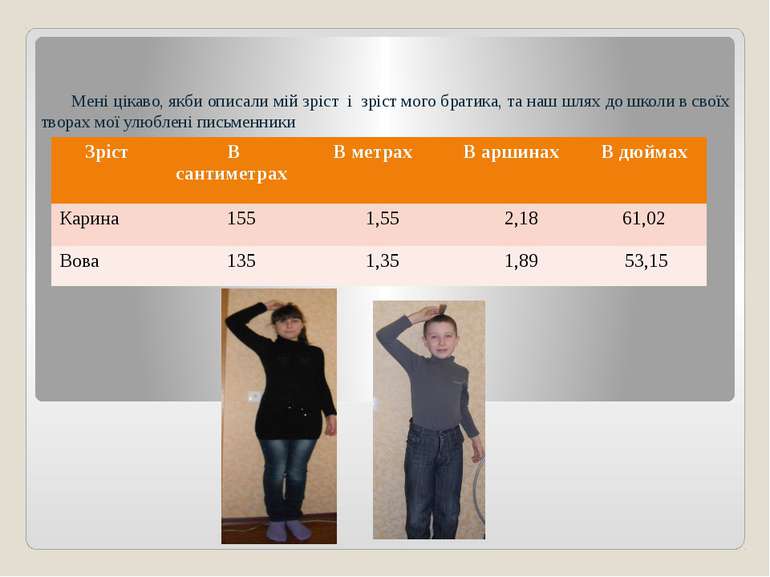
Мені цікаво, якби описали мій зріст і зріст мого братика, та наш шлях до школи в своїх творах мої улюблені письменники Зріст Всантиметрах В метрах В аршинах Вдюймах Карина 155 1,55 2,18 61,02 Вова 135 1,35 1,89 53,15

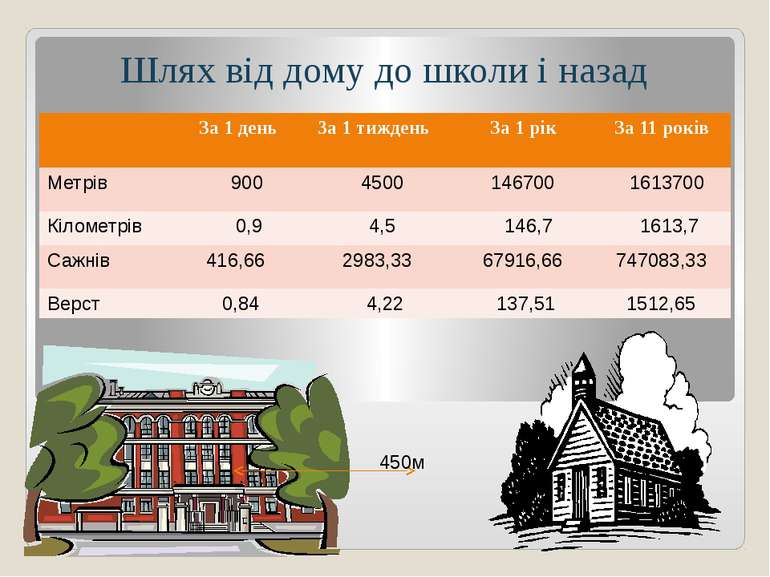
Шлях від дому до школи і назад 450м За 1 день 3а 1 тиждень За 1 рік За 11 років Метрів 900 4500 146700 1613700 Кілометрів 0,9 4,5 146,7 1613,7 Сажнів 416,66 2983,33 67916,66 747083,33 Верст 0,84 4,22 137,51 1512,65

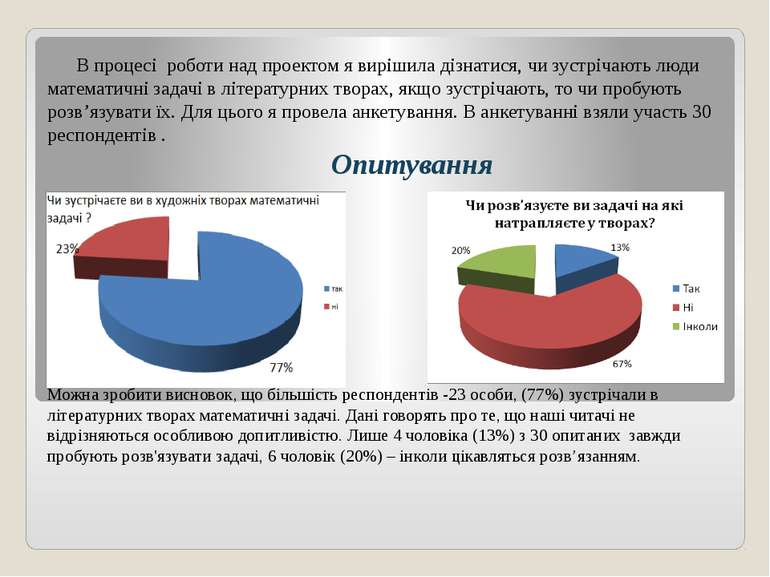
В процесі роботи над проектом я вирішила дізнатися, чи зустрічають люди математичні задачі в літературних творах, якщо зустрічають, то чи пробують розв’язувати їх. Для цього я провела анкетування. В анкетуванні взяли участь 30 респондентів . Опитування Можна зробити висновок, що більшість респондентів -23 особи, (77%) зустрічали в літературних творах математичні задачі. Дані говорять про те, що наші читачі не відрізняються особливою допитливістю. Лише 4 чоловіка (13%) з 30 опитаних завжди пробують розв'язувати задачі, 6 чоловік (20%) – інколи цікавляться розв’язанням.

ВИСНОВКИ Розпочинаючи роботу, я ставила перед собою мету: довести існування зв'язку між літературою та математикою. Для цього: • була вивчена наукова і науково - популярна література, що досліджує зв'язок між літературою та математикою; • були підібрані уривки творів класиків художньої літератури, в яких розглядались або були представлені різні математичні задачі або ситуації, пов'язані з цією наукою; • виконано розв’язання відібраних задач; • проведено порівняння умов і розв’язання задач з дійсністю. Будь-яка книга відкриє свої таємниці тій людині, хто вміє дивитися і бачити, тому, хто вміє дивуватися і сприймати нове, тому, хто вміє сам добувати знання і відповідати на питання, що цікавлять . Математику і літературу можна назвати двома доповнюючими один одного протилежностями. Це дві грані одного і того ж процесу - творчості. Таким чином, мета мого проекту досягнута. Я довела, що між математикою і літературою існує нерозривний зв'язок.

Джерела інформації Довідник Художня література Інтернет