Презентація на тему:
Системи числення

Відповіді до завдання №10

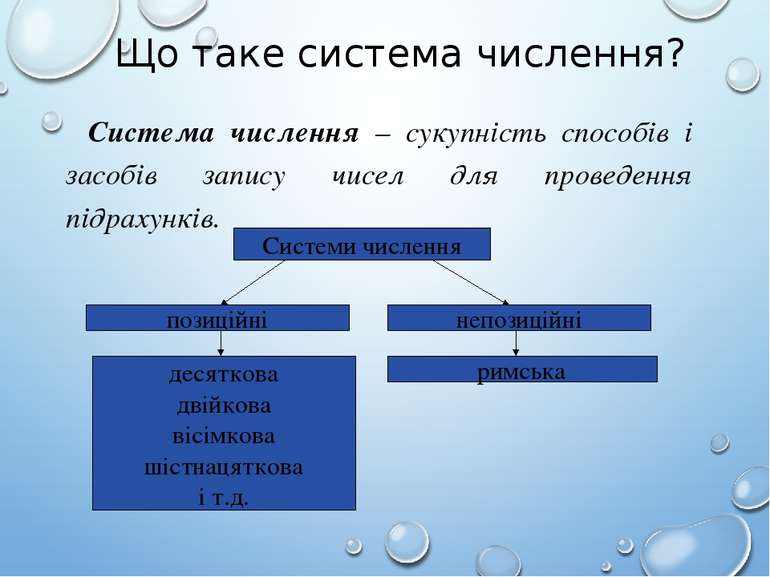
Що таке система числення? Система числення – сукупність способів і засобів запису чисел для проведення підрахунків. десяткова двійкова вісімкова шістнацяткова і т.д.

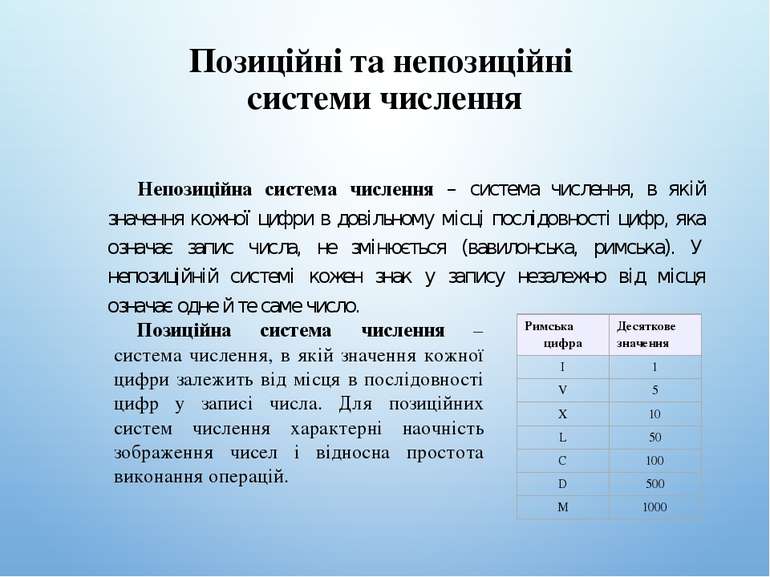
Позиційні та непозиційні системи числення Непозиційна система числення – система числення, в якій значення кожної цифри в довільному місці послідовності цифр, яка означає запис числа, не змінюється (вавилонська, римська). У непозиційній системі кожен знак у запису незалежно від місця означає одне й те саме число. Позиційна система числення – система числення, в якій значення кожної цифри залежить від місця в послідовності цифр у записі числа. Для позиційних систем числення характерні наочність зображення чисел і відносна простота виконання операцій. Римська цифра Десяткове значення I 1 V 5 X 10 L 50 C 100 D 500 M 1000

Римська система числення Непозиційна система числення – кожний символ означає одне і те ж число не залежно від позиції; Цифри позначаються латинскими буквами: I, V, X, L, C, D, M (1, 5, 10, 50, 100, 500, 1000) Наприклад: XXX – 30; XLI - 41

Позиційні системи числення Основою системи може бути довільне натуральне число, більше одиниці; Основа ПСЧ – це кількість цифр, що використовуються для представлення чисел; Значення цифри залежить від її позиції, тобто, одна і та ж цифра відповідає різним значенням в залежності від того на якій позиції числа вона стоїть; Наприклад: 888: 800; 80; 8 Довільне позиційне число можна представити у вигляді суми степеней основи системи.

Десяткова СЧ Основа системи - число 10; Містить10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; Довільне число можна представити у вигляді суми степеней числа 10 – основи системи;

Двійкова СЧ Основа системи – 2; Містить 2 цифри: 0; 1; Довільне двійкове число можна представити у вигляді суми степеней числа 2 – основи системи; Приклади двійкових чисел: 11100101; 10101;

Правила переходу З десяткової СЧ у двійкову СЧ: Розділити десяткове число на 2. Отримаєте частку та остачу. Частку знову поділити на 2. Отримаєте частку та остачу. Виконувати ділення до тих пір, поки остання частка не стане меньшим 2. Записати останню частку і всі остачі у зворотньому порядку. Отримане число і буде двійковим кодом даного десяткового числа.

Приклад:

Завдання № 1: Для десяткових чисел 341; 125; 1024; 4095 виконайте переведення у двійкову систему числення. перевірка

2. Правило переходу з двійкової системи числення у десяткову. Для переходу з двійкової системи числення у десяткову необхідно двійкове число представити у вигляді суми степеней двійки та порахувати її десяткове значення. Приклад:

Завдання № 2: Двійкові числа 1011001, 11110, 11011011 перевести у десяткову систему. перевірка

Вісімкова СЧ Основа системи – 8; Містить 8 цифр: 0; 1; 2; 3; 4; 5; 6; 7; Довільне вісімкове число можна представити у вигляді суми степеней числа 8 – основи системи; Приклади вісімкових чисел: 2105; 73461;

Правило переходу з десяткової системи числення у вісімкову Разділити десяткове число на 8. Отримаєте частку та остачу. Частку знову разділити на 8. Отримаєте частку та остачу. Виконуйте ділення до тих пір, поки остання частка не стане меньшим 8. Записати останню частку та всі остачі у зворотньому порядку. Отримане число і буде вісімковим записом даного десяткового числа.

Приклад:

Завдання № 3: Десяткові числа 421, 5473, 1061 перевести у вісімкову систему. перевірка

Правило переходу з вісімкової системи числення у десяткову. Для переходу з вісімкової системи числення у десяткову необхідно вісімкове число представить у вигляді суми степеней 8 та знайти її десяткове значення.

Завдання № 4: Вісімкові числа 41, 520, 306 перевести у десяткову систему. перевірка

Шістнадцяткова СЧ Основа системи – 16; Містить 16 цифр: от 0 до 9; A; B; C; D; E; F; Довільне шістнадцяткове число можно представити у вигляді суми степеней числа 16 – основи системи; Приклади шістнадцяткових чисел: 21AF3; B09D;

Правило переходу з десяткової системи числення у шістнадцяткову Розділити десяткове число на 16. Отримаєте частку та остачу. Частку знову разділити на 16. Отримаєте частку та остачу. Виконуйте ділення до тих пір, поки остання частка не стане меньшою 16. Записати останню частнку та всі остачі у зворотньому порядку. Отримане число і буде шістнадцятковим кодом даного десяткового числа.

Приклад:

Завдання № 5: Десяткові числа 512, 302, 2045 перевести у шістнадцяткову систему. перевірка

Правило переходу з шістнадцяткової системи числення у десяткову. Для переходу з шістнадцяткової системи числення у десяткову необхідино дане число представити у вигляді суми степеней шістнацятки та обчислити її десяткові значення.

Завдання № 6: Шістнадцяткові числа B5, A28,CD перевести у десяткову систему. перевірка

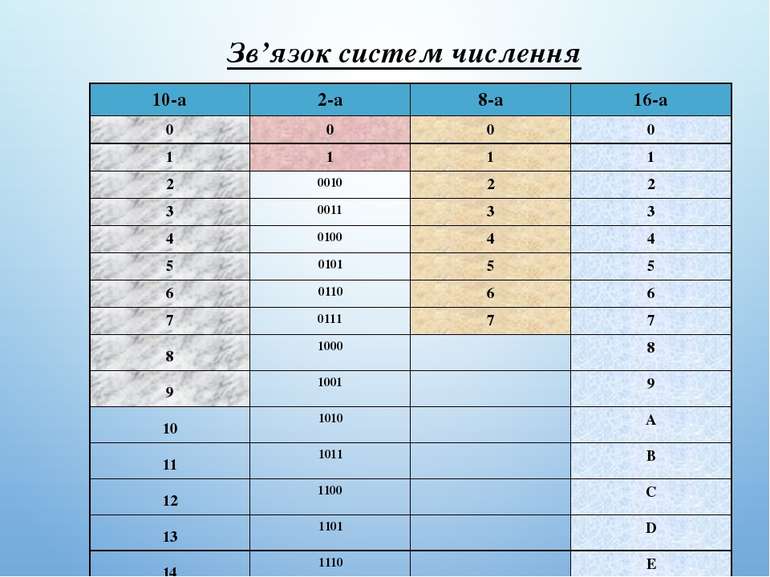
Зв’язок систем числення 10-а 2-а 8-а 16-а 0 0 0 0 1 1 1 1 2 0010 2 2 3 0011 3 3 4 0100 4 4 5 0101 5 5 6 0110 6 6 7 0111 7 7 8 1000 8 9 1001 9 10 1010 A 11 1011 B 12 1100 C 13 1101 D 14 1110 E 15 1111 F

Правило переходу з двійкової системи числення у вісімкову Розбити двійковий код на класи справа на ліво по три цифри у кожному. Замінити кожний клас відповідною вісімковою цифрой.

Завдання № 7: Двійкові числа 10101111, 11001100110 перевести у вісімкову систему перевірка

Правило переходу з вісімкової системи числення у двійкову Кожну вісімкову цифру замінити двійковим кодом по три цифри у кожному

Завдання № 8: Вісімкові числа 26, 702, 4017 перевести у двійкову систему. перевірка

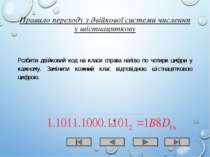
Правило переходу з двійкової системи числення у шістнацяткову Розбити двійковий код на класи справа наліво по чотири цифри у кажному. Замінити кожний клас відповідною шістнацятковою цифрою.

Завдання № 9: Двійкові числа 10101111, 11001100110 перевести у шістнацяткову систему перевірка

Правило переходу з шістнацяткової системи числення у двійкову Кожну шістнацяткову цифру замінити двійковим кодом по чотири цифри у кожному

Завдання № 10: Шістнацяткові числа C3, B096, E38 перевести у двійкову систему. перевірка

Завдання для домашньої роботи Для кожного з чисел: 12310, 45610 виконати переведення: 10 2, 10 8, 10 16. Для кожного з чисел : 1000112, 1010010112, 11100100012 виконати переведення : 2 10, 2 8, 2 16. Для чисел: 543218, 545258, 7778, 1AB16, A1B16, E2E416, E7E516 виконати переведення: 8 2, 16 2.